C TEVA DEMONSTRAII ALE TEOREMEI LUI PITAGORA ENUN

C TEVA DEMONSTRAŢII ALE TEOREMEI LUI PITAGORA ENUNŢ: , , În orice triunghi dreptunghic, pătratul lungimii ipotenuzei este egal cu suma pătratelor lungimilor catetelor’’ V. P.

• Pitagora ( 580 î. Hr. - 500 î. Hr. ) a fost un filozof şi matematician grec, originar din insula Samos, întemeietorul pitagorismului, care punea la baza întregii realităţi teoria numerelor şi a armoniei. A fost şi conducătorul partidului aristocratic din Crotone (sudul Italiei). Scrierile sale nu s-au păstrat. Tradiţia îi atribuie descoperirea teoremei geometrice şi a tablei de înmulţire, care îi poartă numele. Ideile şi descoperirile lui nu pot fi deosebite cu certitudine de cele ale discipolilor apropiaţi. • Pitagora era ionian, originar din insula Samos, dar a emigrat la Crotone, în Italia de sud, unde a întemeiat şcoala ce-i poartă numele, cea dintîi şcoală italică a Greciei antice • Pitagora a fost un mare educator şi învăţător al spiritului grecesc şi se spune că a fost şi un atlet puternic, aşa cum stătea bine atunci poeţilor, filosofilor (de exemplu, Platon însuşi) şi comandanţilor militari etc. • Pitagora pare să nu fi scris nimic. Doctrina filosofică a pitagorismului ne este totuşi destul de bine cunoscută din lucrările lui Aristotel şi Sextus Empiricus, precum şi din lucrări ale pitagoricienilor de mai tîrziu. Totuşi, nu se poate stabili cu precizie ce aparţine lui Pitagora şi ce au adăugat pitagoricienii ulteriori. Celebrele texte "pitagoriciene" Versurile de aur ale lui Pitagora şi Legile morale şi politice ale lui

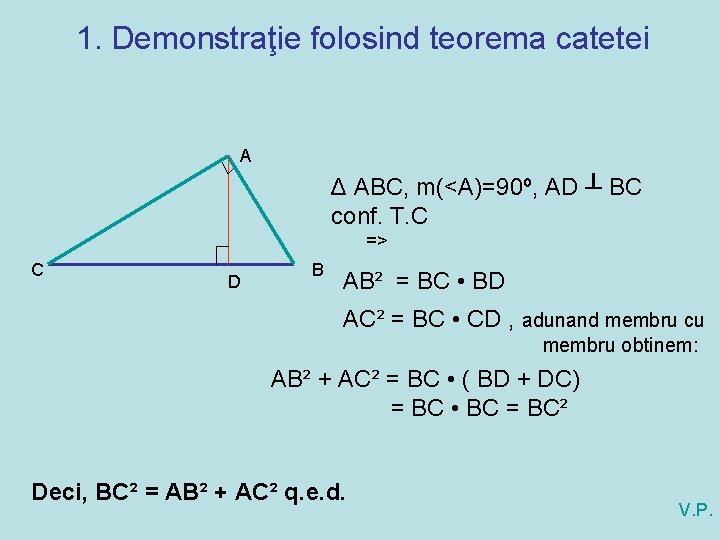
1. Demonstraţie folosind teorema catetei A Δ ABC, m(<A)=90º, AD ┴ BC conf. T. C => C D B AB² = BC • BD AC² = BC • CD , adunand membru cu membru obtinem: AB² + AC² = BC • ( BD + DC) = BC • BC = BC² Deci, BC² = AB² + AC² q. e. d. V. P.

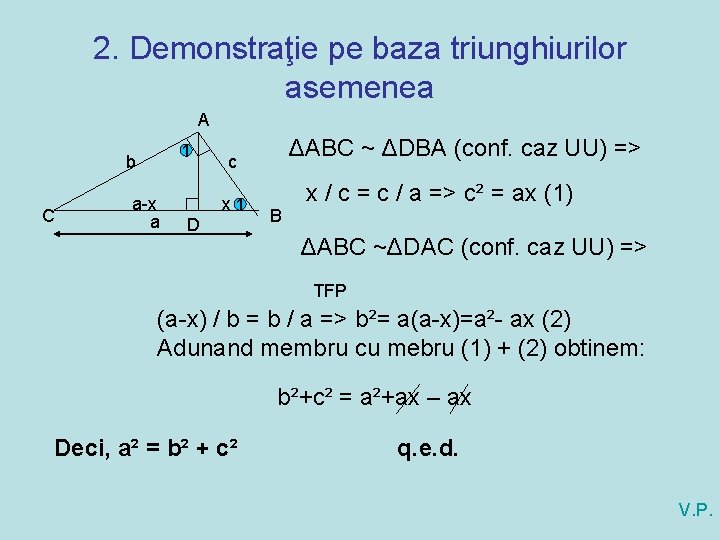
2. Demonstraţie pe baza triunghiurilor asemenea A 1 b C a-x a ΔABC ~ ΔDBA (conf. caz UU) => c x 1 D B x / c = c / a => c² = ax (1) ΔABC ~ΔDAC (conf. caz UU) => TFP (a-x) / b = b / a => b²= a(a-x)=a²- ax (2) Adunand membru cu mebru (1) + (2) obtinem: b²+c² = a²+ax – ax Deci, a² = b² + c² q. e. d. V. P.

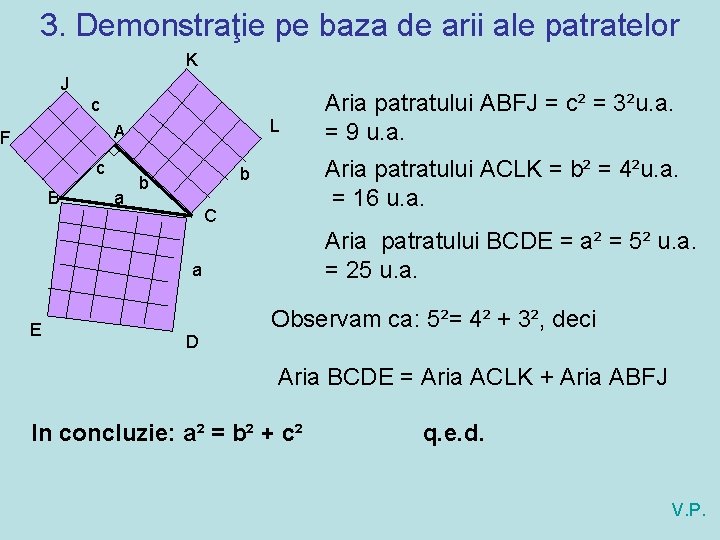
3. Demonstraţie pe baza de arii ale patratelor K J c L A F c B a Aria patratului ACLK = b² = 4²u. a. = 16 u. a. b b C Aria patratului BCDE = a² = 5² u. a. = 25 u. a. a E D Aria patratului ABFJ = c² = 3²u. a. = 9 u. a. Observam ca: 5²= 4² + 3², deci Aria BCDE = Aria ACLK + Aria ABFJ In concluzie: a² = b² + c² q. e. d. V. P.

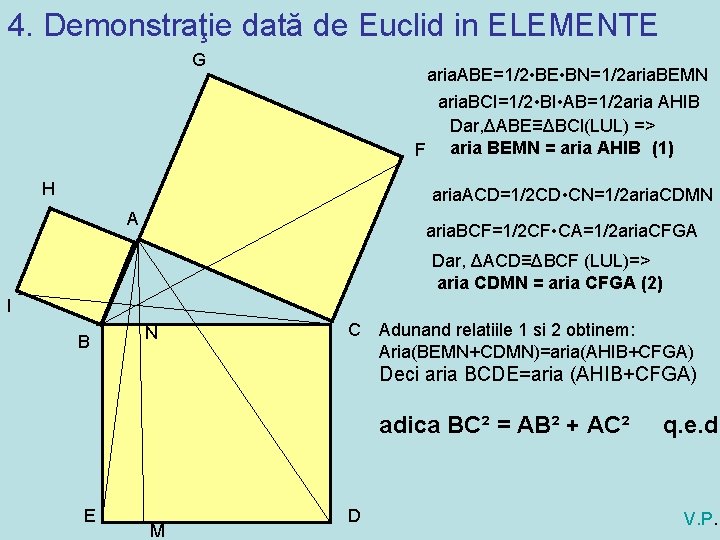
4. Demonstraţie dată de Euclid in ELEMENTE G aria. ABE=1/2 • BE • BN=1/2 aria. BEMN aria. BCI=1/2 • BI • AB=1/2 aria AHIB Dar, ΔABE≡ΔBCI(LUL) => F aria BEMN = aria AHIB (1) H aria. ACD=1/2 CD • CN=1/2 aria. CDMN A aria. BCF=1/2 CF • CA=1/2 aria. CFGA Dar, ΔACD≡ΔBCF (LUL)=> aria CDMN = aria CFGA (2) I B N C Adunand relatiile 1 si 2 obtinem: Aria(BEMN+CDMN)=aria(AHIB+CFGA) Deci aria BCDE=aria (AHIB+CFGA) adica BC² = AB² + AC² E M D q. e. d. V. P.

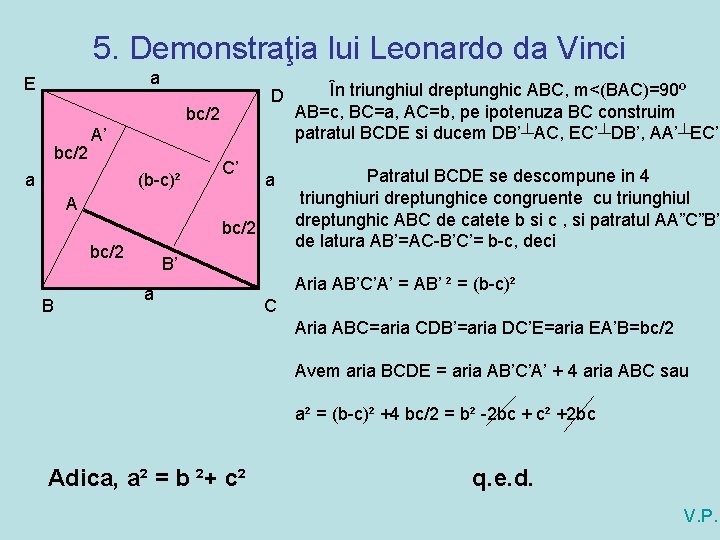
5. Demonstraţia lui Leonardo da Vinci a E D bc/2 A’ a (b-c)² C’ a A bc/2 B În triunghiul dreptunghic ABC, m<(BAC)=90º AB=c, BC=a, AC=b, pe ipotenuza BC construim patratul BCDE si ducem DB’┴AC, EC’┴DB’, AA’┴EC’. Patratul BCDE se descompune in 4 triunghiuri dreptunghice congruente cu triunghiul dreptunghic ABC de catete b si c , si patratul AA”C”B” de latura AB’=AC-B’C’= b-c, deci B’ a Aria AB’C’A’ = AB’ ² = (b-c)² C Aria ABC=aria CDB’=aria DC’E=aria EA’B=bc/2 Avem aria BCDE = aria AB’C’A’ + 4 aria ABC sau a² = (b-c)² +4 bc/2 = b² -2 bc + c² +2 bc Adica, a² = b ²+ c² q. e. d. V. P.

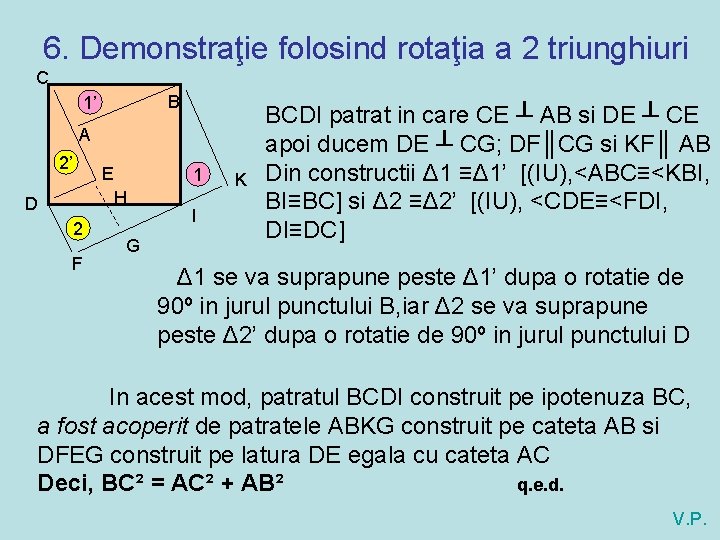
6. Demonstraţie folosind rotaţia a 2 triunghiuri C B 1’ A 2’ E 1 H D 2 F G I K BCDI patrat in care CE ┴ AB si DE ┴ CE apoi ducem DE ┴ CG; DF║CG si KF║ AB Din constructii Δ 1 ≡Δ 1’ [(IU), <ABC≡<KBI, BI≡BC] si Δ 2 ≡Δ 2’ [(IU), <CDE≡<FDI, DI≡DC] Δ 1 se va suprapune peste Δ 1’ dupa o rotatie de 90º in jurul punctului B, iar Δ 2 se va suprapune peste Δ 2’ dupa o rotatie de 90º in jurul punctului D In acest mod, patratul BCDI construit pe ipotenuza BC, a fost acoperit de patratele ABKG construit pe cateta AB si DFEG construit pe latura DE egala cu cateta AC Deci, BC² = AC² + AB² q. e. d. V. P.

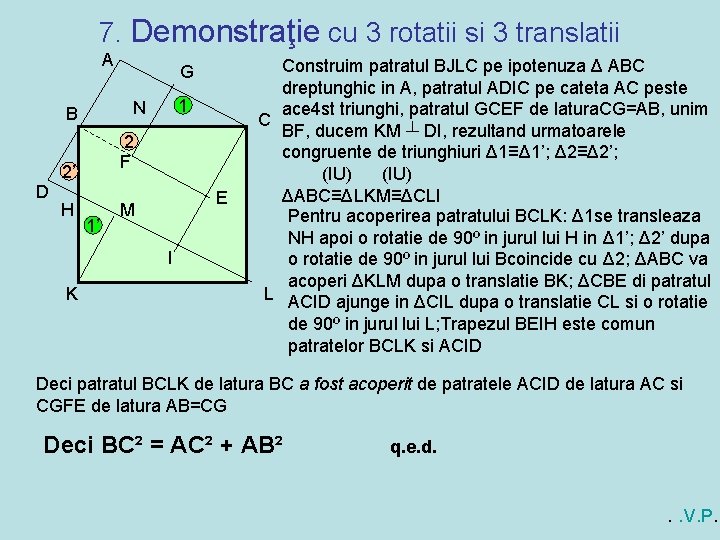
7. Demonstraţie cu 3 rotatii si 3 translatii A 2 F 2’ H 1 N B D G 1’ E M I K Construim patratul BJLC pe ipotenuza Δ ABC dreptunghic in A, patratul ADIC pe cateta AC peste ace 4 st triunghi, patratul GCEF de latura. CG=AB, unim C BF, ducem KM ┴ DI, rezultand urmatoarele congruente de triunghiuri Δ 1≡Δ 1’; Δ 2≡Δ 2’; (IU) ΔABC≡ΔLKM≡ΔCLI Pentru acoperirea patratului BCLK: Δ 1 se transleaza NH apoi o rotatie de 90º in jurul lui H in Δ 1’; Δ 2’ dupa o rotatie de 90º in jurul lui Bcoincide cu Δ 2; ΔABC va acoperi ΔKLM dupa o translatie BK; ΔCBE di patratul L ACID ajunge in ΔCIL dupa o translatie CL si o rotatie de 90º in jurul lui L; Trapezul BEIH este comun patratelor BCLK si ACID Deci patratul BCLK de latura BC a fost acoperit de patratele ACID de latura AC si CGFE de latura AB=CG Deci BC² = AC² + AB² q. e. d. . . V. P.

8. Demonstraţie folosind descompunerea unui trapez dreptunghic E b D In trapezul dreptunghic ABDE avem m(<A)=m(<E)=90º, AB=CE=c, DE=AC=b, AC+CE=b+c (m(<BCD) =90º) bc/2 c a a²/2 C b bc/2 a A c B Aria ABDE = ½ (AB+DE) • AE=½ (b+c)= ½ (b+c)² Aria ABDE = aria ABC +aria CDE+aria. BCD= = bc/2 + ½ • a²/2 = ½ (2 bc + a²) Deci (b+c)²= 2 bc + a² sau b²+2 bc+c² = 2 bc + a² Intradevăr, a² = b² + c² q. e. d.

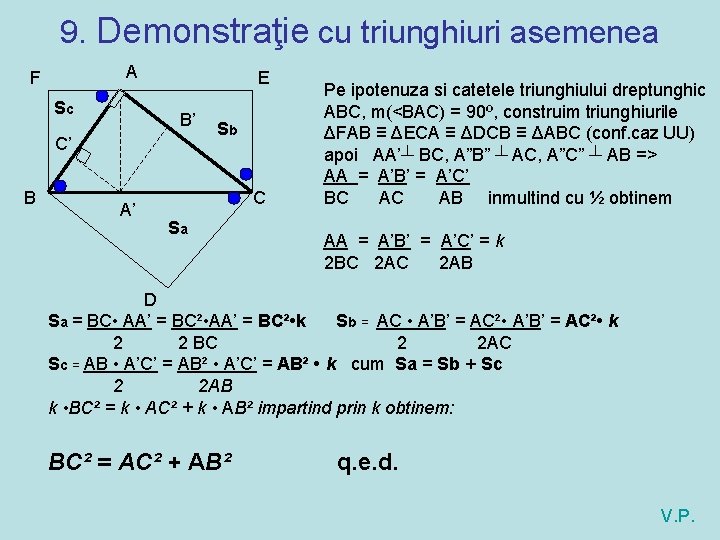
9. Demonstraţie cu triunghiuri asemenea A F Sc E B’ C’ B A’ Sb C Sa Pe ipotenuza si catetele triunghiului dreptunghic ABC, m(<BAC) = 90º, construim triunghiurile ΔFAB ≡ ΔECA ≡ ΔDCB ≡ ΔABC (conf. caz UU) apoi AA’┴ BC, A”B” ┴ AC, A”C” ┴ AB => AA = A’B’ = A’C’ BC AC AB inmultind cu ½ obtinem AA = A’B’ = A’C’ = k 2 BC 2 AB D Sa = BC • AA’ = BC² • k Sb = AC • A’B’ = AC² • k 2 2 BC 2 2 AC Sc = AB • A’C’ = AB² • k cum Sa = Sb + Sc 2 2 AB k • BC² = k • AC² + k • AB² impartind prin k obtinem: BC² = AC² + AB² q. e. d. V. P.

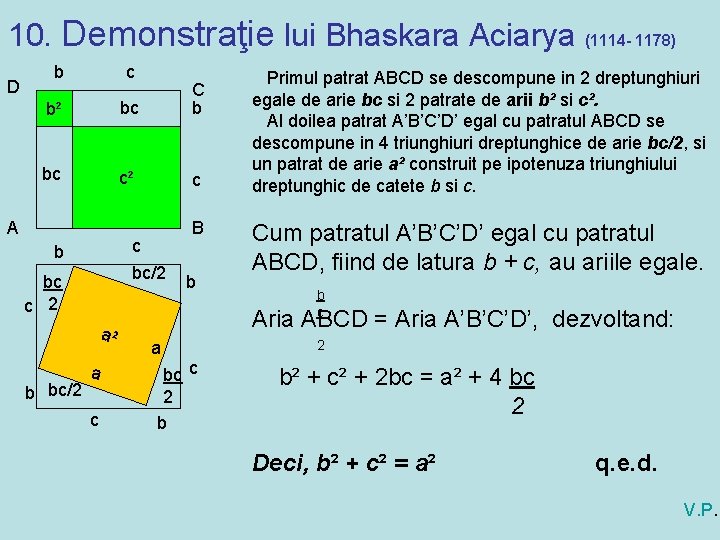
10. Demonstraţie lui Bhaskara Aciarya (1114 - 1178) D b c b² bc C b bc c² c A c b bc/2 bc c 2 a² b bc/2 B a c b Primul patrat ABCD se descompune in 2 dreptunghiuri egale de arie bc si 2 patrate de arii b² si c². Al doilea patrat A’B’C’D’ egal cu patratul ABCD se descompune in 4 triunghiuri dreptunghice de arie bc/2, si un patrat de arie a² construit pe ipotenuza triunghiului dreptunghic de catete b si c. Cum patratul A’B’C’D’ egal cu patratul ABCD, fiind de latura b + c, au ariile egale. b c Aria ABCD = Aria A’B’C’D’, dezvoltand: a bc c 2 b² + c² + 2 bc = a² + 4 bc 2 Deci, b² + c² = a² q. e. d. V. P.

, , Învăţând matematică, înveţi să gândeşti’’. citat din Grigore Moisil , , Geometria este cea mai bună şi mai simplă dintre toate logicile, cea mai potrivită să dea inflexibilitate judecăţii şi raţiunii. ’’ definiţie de Denis Diderot