BINARY ARITHMETIC Binary Addition Binary Subtraction Modern Binary

BINARY ARITHMETIC ¡Binary Addition ¡Binary Subtraction

Modern Binary Number System ¡ The modern binary number system was fully documented by Gottfried Leibniz in the 17 th century in his article Explication de l'Arithmétique Binaire. Leibniz's system used 0 and 1, like the modern binary numeral system.

¡ He also discovered the binary system, foundation of virtually all modern computer architectures. In philosophy, he is mostly remembered for optimism, i. e. his conclusion that our universe is, in a restricted sense, the best possible one God could have made. From Wikipedia.

Why are we learning about Binary? ¡ Because at a very base level, that’s how computers work. ¡ They add stuff up etc…. all on the basis of things being ON (1) or OFF(0) ¡ So Binary is crucial to understanding the basics of how Computers work ¡ Genetics –also important when studying the human body! (DNA…RNA…Code!)
In the days before computers Developing processors with circuitry That performed calculations…all in binary!

The questions they had to ask themselves were I want the computer to add 2+ 3 – how do I do it? ¡ First, how do I display the number 2 or 3? (in terms of 1’s and 0’s) ¡ Second how do I add these two numbers together ¡ What if I had a negative number. . how would I represent that in 1’s and 0’s? ¡

John Vincent Atanasoff? ? died 15 June 1995. KONRAD ZUSE (1910 -1995) Konrad Zuse builds Z 1, world's first program-controlled computer. Said to have built it in the living room of his Parents apartment in BERLIN! 1946: Zuse founds world's first computer startup company: the Zuse. Ingenieurbüro Hopferau. Venture capital raised through ETH Zürich and an IBM option on Zuse's patents. Credited with being the inventor of the first programmable computer!

1950: Despite having lost many years of work through the destruction of Berlin, Zuse leases world's first commercial computer (the Z 4) to ETHZ, several months before the sale of the first UNIVAC. From http: //www. idsia. ch/~juergen/zuse. html

Zuse’s wild ideas. ¡ Read more about them…all his writings, and musings and thoughts etc at: http: //www. zib. de/zuse/English_Version/i ndex. html (online archive of interesting stuff he did/wrote)

Zuse’s computer used the Binary System! ¡ Interesting Facts Konrad Zuse wrote the first algorithmic programming language called 'P The Plankalkül language included arrays and records and used a style of assignment (storing the value of an expression in a variable) in which the new value appears in the right column. An array is a collection of identically typed data items distinguished by their indices (or "subscripts"), for example written something like A[i, j, k], where A is the array name and i, j and k are the indices. Arrays are best when accessed in an unpredictable order. This is in contrast to lists, which are best when accessed sequentially. Zuse was unable to convince the Nazi government to support his work for a computer based on electronic valves. The Germans thought they were close to winning the War and felt no need to support further research.

Another Interesting fact. ¡ By 1967, the Zuse KG had built a total of 251 computers. Due to financial problems, it was then sold to Siemens. Well known company today

¡ ¡ ¡ Claude Shannon Claude Elwood Shannon (April 30, 1916 – February 24, 2001), an American electronic engineer and mathematician, is "the father of information theory". [1] Shannon is famous for having founded information theory with one landmark paper published in 1948. But he is also credited with founding both digital computer and digital circuit design theory in 1937, when, as a 21 -year-old master's student at MIT, he wrote a thesis demonstrating that electrical application of Boolean algebra could construct and resolve any logical, numerical relationship. It has been claimed that this was the most important master's thesis of all time. [2] http: //en. wikipedia. org/wiki/Claude_Shannon

Binary! We’ve discussed already how to reprsent Decimal numbers as Binary numbers and vice versa. 3 in Decimal (base 10) is 011 in Binary ¡ Now…what about Arithmetic in Binary!? ! What is 10010101 + 1010? !

Binary Addition ¡ The last entry in the above table should be read as "1 + 1 = 0 with a carry of 1", analogous to the decimal system where 9 + 1 = 0 with a carry of 1 = 10. • Just as we read decimal 12 to be 1 X 101 + 2 X 10 0, the last entry, • "10" is to be read as "one times 21 plus 0 times 20".
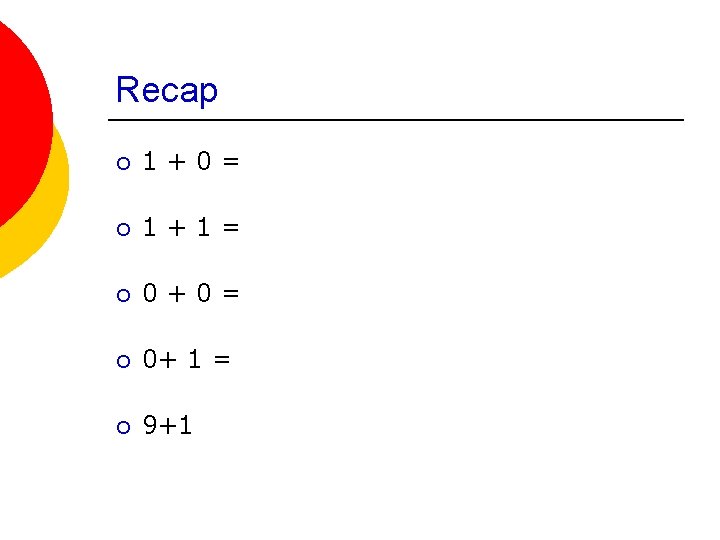
Recap ¡ 1+0= ¡ 1+1= ¡ 0+0= ¡ 0+ 1 = ¡ 9+1

Recap on Converting Binary + Decimal ¡ 128 1 64 0 32 1 16 0 8 4 2 1 0 1 1 0 This equals 128 + 16 + 4 + 2 = 150

Converting a two’s compliment number into DENARY ¡ Left most bit has a negative place value. -128 1 64 0 32 1 16 0 8 4 2 1 0 1 1 0 This equals -128 + 16 + 4 + 2 = -106

Ordinary denary subtraction ¡ 0 -0= ¡ 1 -1= ¡ 0 -1=
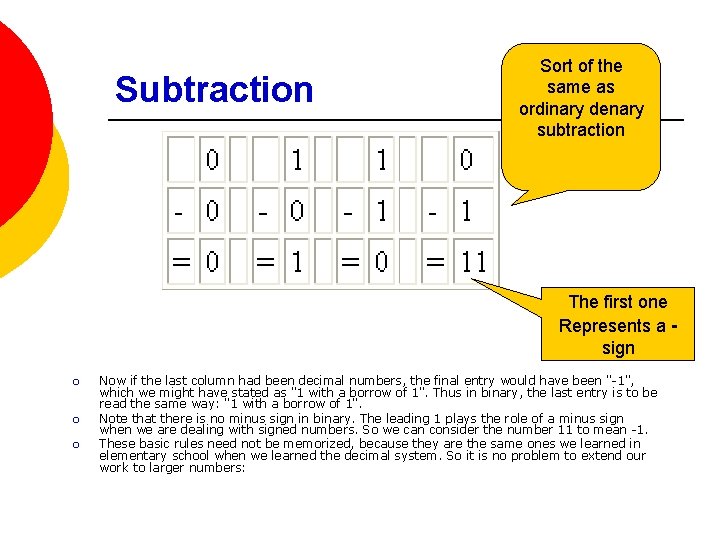
Subtraction Sort of the same as ordinary denary subtraction The first one Represents a sign ¡ ¡ ¡ Now if the last column had been decimal numbers, the final entry would have been "-1", which we might have stated as "1 with a borrow of 1". Thus in binary, the last entry is to be read the same way: "1 with a borrow of 1". Note that there is no minus sign in binary. The leading 1 plays the role of a minus sign when we are dealing with signed numbers. So we can consider the number 11 to mean -1. These basic rules need not be memorized, because they are the same ones we learned in elementary school when we learned the decimal system. So it is no problem to extend our work to larger numbers:

The easiest way To subtract binary numbers ¡ 1) Convert the number to be subtracted to a negative number…and then add it. ¡ So to subtract 12 from 15 1)Convert 12 to Negative binary number 2) Add 15 (in binary to 12) ¡
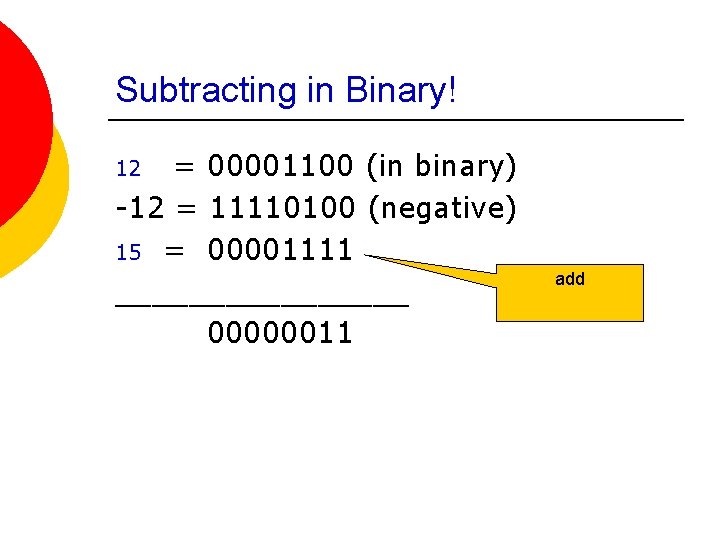
Subtracting in Binary! = 00001100 (in binary) -12 = 11110100 (negative) 15 = 00001111 ________ 00000011 12 add

What are they!? ¡ Integers –whole numbers, ¡ Real Numbers –fractions or 1. 10 ¡ Floating Point –a system for numerical representation of real numbers (a string of digits represents a real number –the point can float)

MSB –Most Significant Bit

Sign and Magnitude A value can be represented using SIGN and MAGNITUDE ¡ 1 bit (1 or 0) represents the SIGN of the number. 1= -1 and 0 =positive number ¡ For example: 1010 = -2 0010 = +2

What is the disadvtange of this? For example: 1010 = -2 0010 = +2 ¡ ¡ What is the maximum number it can hold? (maximum VALUE 4 bits can hold) How many digits can 4 bits hold? If there was no sign bit, what is the max number? If there was no sign bit, what is the maximum digits? 15 (-7 to 7) 16 (0 -15) 15 16 (0 -15) 7

What is the disadvtange of this? For example: 1010 = -2 0010 = +2 ¡ ¡ What is the maximum number it can hold? (maximum VALUE 4 bits can hold) 7 How many digits can 4 bits hold? 15 (-7 to 7) If there was no sign bit, what is the max number? 15 If there was no sign bit, what is the maximum digits? 16 (0 -15)

4 bits can represent either 1111 0000 or a combination of 1’s and 0’s Without sign bit -7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4 , 5, 6, 7 With sign bit 0, 1, 2, 3, 4, 5 , 6, 7, 8, 9, 10, 11, 12, 13, 14, 15

4 bits can represent either 1111 0000 or a combination of 1’s and 0’s Can hold only 15 digits With sign bit -7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4 , 5, 6, 7 Without sign bit Can hold 16 digits 0, 1, 2, 3, 4, 5 , 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 8421 1111 Why can you only hold 15 digits (and not 16) When you use sign and magnitude.
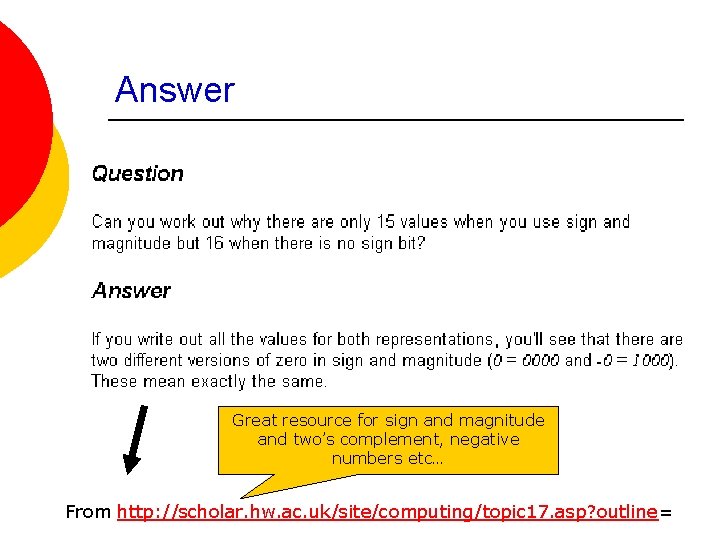
Answer Great resource for sign and magnitude and two’s complement, negative numbers etc… From http: //scholar. hw. ac. uk/site/computing/topic 17. asp? outline=

http: //scholar. hw. ac. uk/site/computing/topic 17. asp? outline=

Here we notice that we DO NOT need an extra bit to represent the sign. In other words, 4 bits can represent -8 as well as +8 (using four bits) So there is no wastage of bits. The advantage of this system is that Positive and negative numbers can be treated in the same way.
Read the tutorial on this site (very useful) ¡ http: //scholar. hw. ac. uk/site/comput ing/topic 18. asp? outline=no

Converting a Binary (positive decimal equivalent) to its negative Is this represented Using sign and magnitude or Two’s complement? Notice the negative

Why do we need to know how to convert to negative!?

What about Addition and Subtraction. What if you somehow went to Primary school and were taught how To ADD, but not how to subtract. How would you deal with subtracting 12 from 15?

Assuming you knew how to deal with negative numbers JOHN SMITH –CV Picture of me -Addition -Knowledge of Negative Numbers -can’t subtract but have developed technique to subtract using negative numbers and addition!
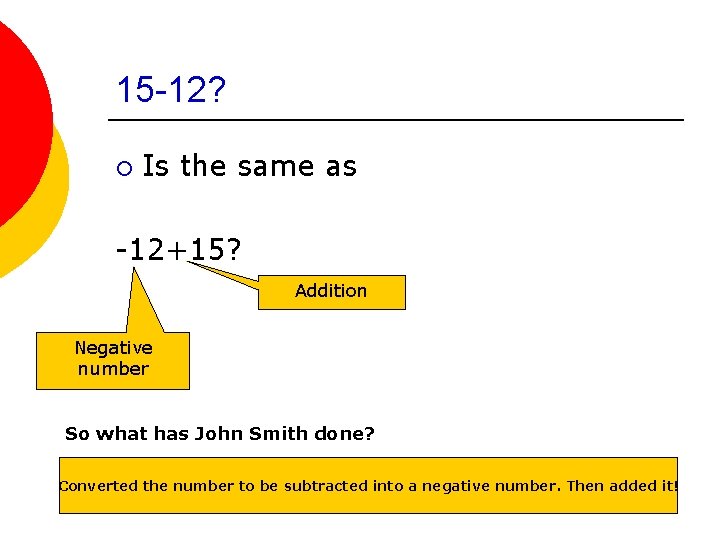
15 -12? ¡ Is the same as -12+15? Addition Negative number So what has John Smith done? Converted the number to be subtracted into a negative number. Then added it!

Computers=John Smith ¡ Instead of Subtracting, they just stick with addition. ¡ But for that they have to first convert the number to be subtracted into a negative number! This is why we need to know HOW to convert a number into a negative equivalent!

- Slides: 39