Binary Arithmetic Binary Arithmetic BCD n Binary n

Binary Arithmetic

Binary Arithmetic BCD n Binary n Unsigned n 1’s complement n 2’s complement n

BCD Example-1 Example-2

Unsigned - Subtraction The subtraction of two n-digit unsigned numbers M-N(N 0) in base r (2) can be done. 1) Add the minuend M to the r’s (2’s) complement of the subtrahend N. This performs M + ( r - N). 2) If M N , the sum will produce an end carry r which is discarded, and what is the left is is the result M-N.

Unsigned - Subtraction (cont. ) 3) If M < N , the sum does not produce an end carry and is equal to r - (N M), which is the r’s complement (2’s) of (N - M). To obtain the answer in a familiar form , take the r’s (2’s) complement of the sum and plant a negative sign in front.

Unsigned - Overflow

Binary Arithmetic n n Two binary numbers can be added, starting at the rightmost bit and adding the corresponding bits in the addend and the augend. If a carry is generated, it is carried one position to the left, just as in decimal arithmetic. In 1’s complement arithmetic, a carry generated by the addition of the leftmost bit is added to the rightmost bit. This process is called an end-around carry. In 2’s complement arithmetic, a carry generated by the addition of the leftmost bits is merely thrown away.

Arithmetic with 1’s Complement (8 Bits) Ex 1: Ex 3: Ex 2:

Arithmetic with 2’s Complement (8 Bits) • Addition: • Subtraction: • Take the 2’s complement of subtrahend (including the sign bit) and add it to the minuend (including the sign bit). A carry out of the sign bit position is discarded. EX: (+6 )- (-13) = (+6) + (+13) , shown above.
Overflow

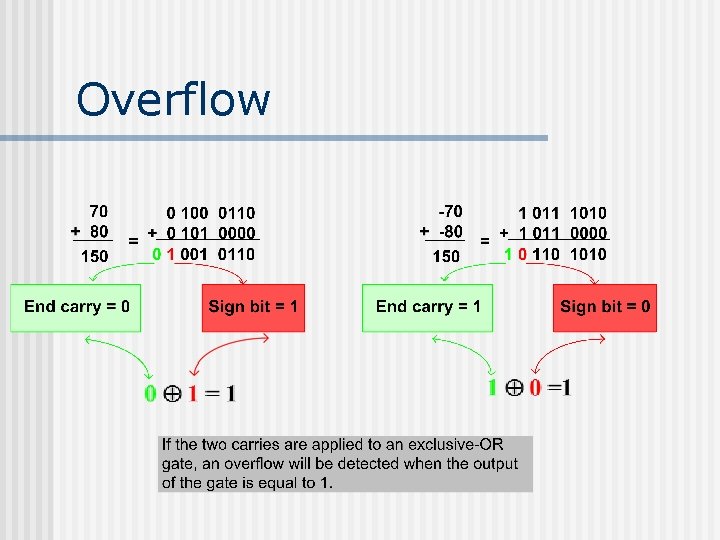
Binary Arithmetic Errors n n n If the addend and the augend are of opposite signs, overflow error can not occur. If they are of the same sign and the result is the opposite sign, overflow has occurred and the answer is wrong. In both 1’s and 2’s complement arithmetic, overflow occurs if and only if the carry into the sign bit differs from the carry out of the sign bit. Most computers preserve the carry out of the sign bit, but the carry into the sign is not visible from the answer. For this reason, a special overflow bit is usually provided.

n Reading : from links n Signed numbers n Floating point numbers
- Slides: 12