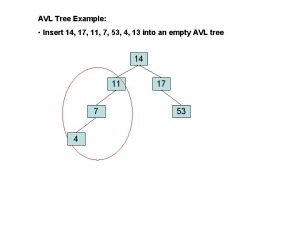
AVL Search Trees Introduction What is an AVL

AVL Search Trees • Introduction • What is an AVL Tree? • AVL Tree Implementation. • Why AVL Trees? • Rotations.

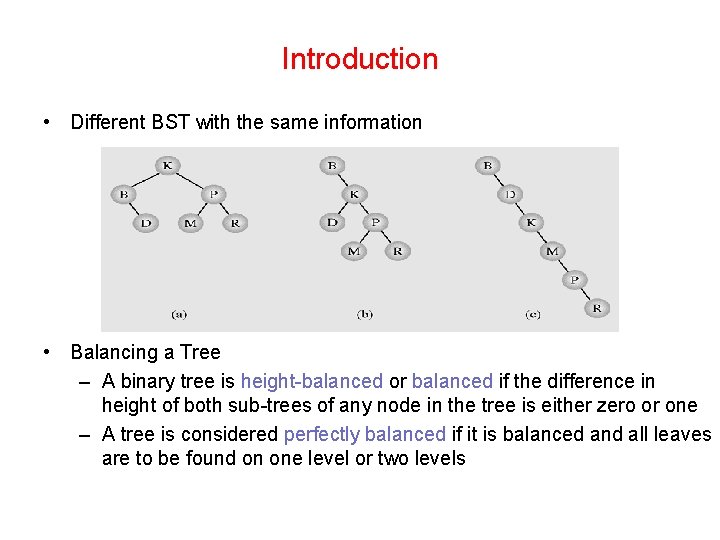
Introduction • Different BST with the same information • Balancing a Tree – A binary tree is height-balanced or balanced if the difference in height of both sub-trees of any node in the tree is either zero or one – A tree is considered perfectly balanced if it is balanced and all leaves are to be found on one level or two levels

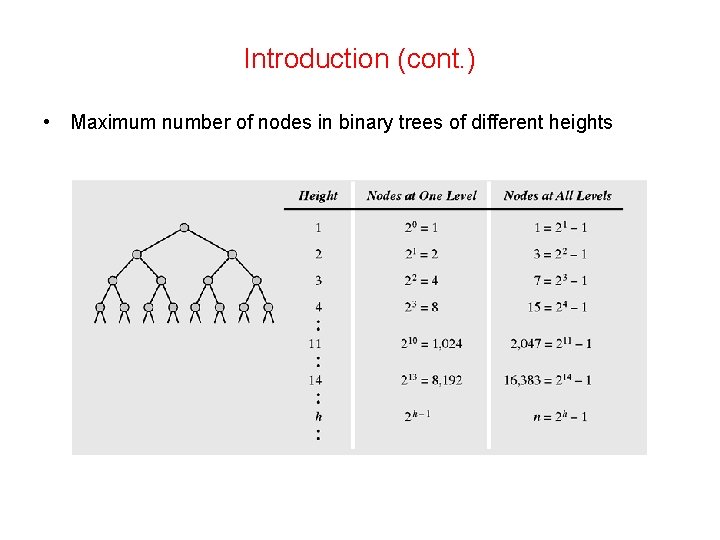
Introduction (cont. ) • Maximum number of nodes in binary trees of different heights

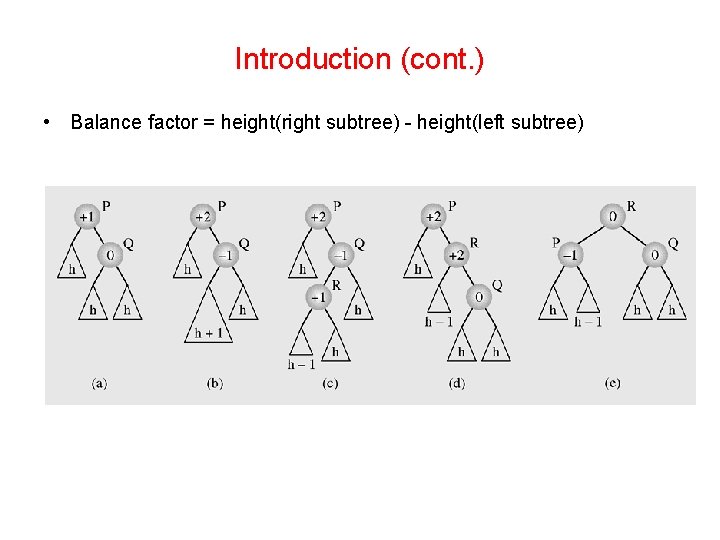
Introduction (cont. ) • Balance factor = height(right subtree) - height(left subtree)

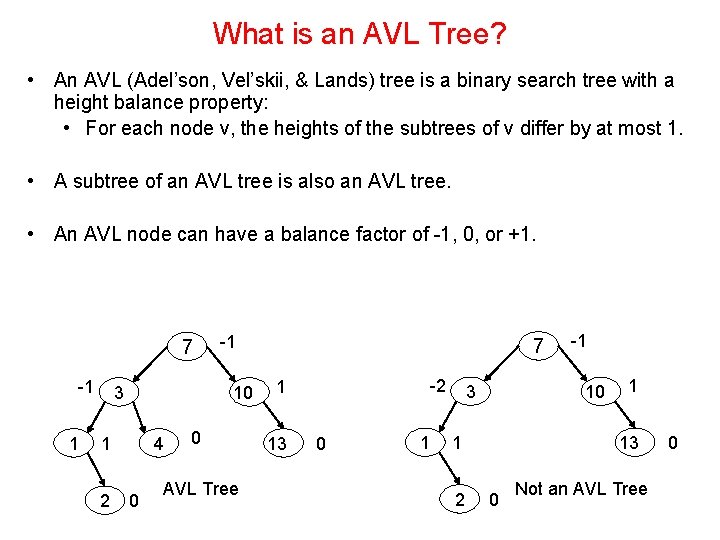
What is an AVL Tree? • An AVL (Adel’son, Vel’skii, & Lands) tree is a binary search tree with a height balance property: • For each node v, the heights of the subtrees of v differ by at most 1. • A subtree of an AVL tree is also an AVL tree. • An AVL node can have a balance factor of -1, 0, or +1. 7 -1 1 3 10 4 1 2 -1 0 0 AVL Tree 7 -2 1 13 0 1 3 10 1 13 1 2 -1 0 Not an AVL Tree 0

AVL Trees Implementation public class AVLTree extends Binary. Search. Tree{ protected int height; public AVLTree(){ height = -1; } public int get. Height(){ return height } ; protected void adjust. Height(){ if(is. Empty()) height = -1; else height = 1 + Math. max(left. get. Height() , right. get. Height()); } protected int get. Balance. Factor(){ if( is. Empty()) return 0; else return right. get. Height() - left. get. Height(); } //. . . }

Why AVL Trees? • Insertion or deletion in an ordinary Binary Search Tree can cause large imbalances. • In the worst case searching an imbalanced Binary Search Tree is O(n). • An AVL tree is rebalanced after each insertion or deletion. • The height-balance property ensures that the height of an AVL tree with n nodes is O(log n). • Searching, insertion, and deletion are all O(log n).

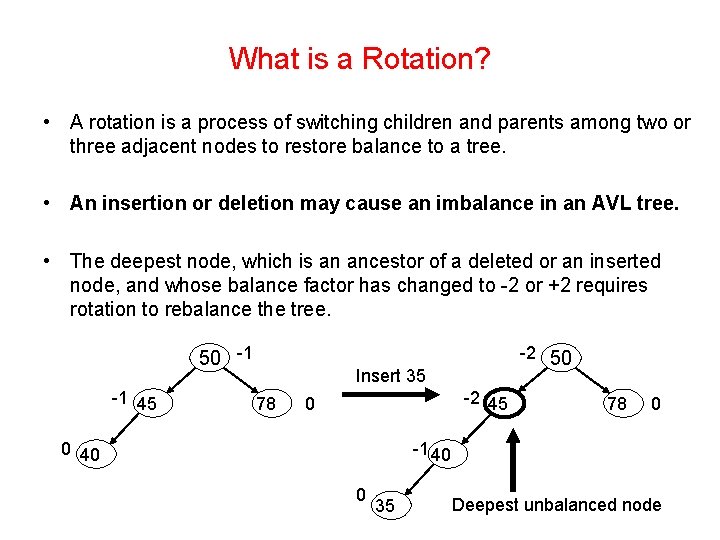
What is a Rotation? • A rotation is a process of switching children and parents among two or three adjacent nodes to restore balance to a tree. • An insertion or deletion may cause an imbalance in an AVL tree. • The deepest node, which is an ancestor of a deleted or an inserted node, and whose balance factor has changed to -2 or +2 requires rotation to rebalance the tree. 50 -1 -1 45 -2 50 Insert 35 78 -2 45 0 0 40 78 0 -1 40 0 35 Deepest unbalanced node

What is a Rotation? (contd. ) -2 -2 45 -1 50 50 rotation 78 -1 40 0 0 35 78 45 0 35 • There are two kinds of single rotation: Right Rotation. Left Rotation. • A double right-left rotation is a right rotation followed by a left rotation. • A double left-right rotation is a left rotation followed by a right rotation. 0

Single Right Rotation • Single right rotation: • The left child x of a node y becomes y's parent. • y becomes the right child of x. • The right child T 2 of x, if any, becomes the left child of y. deepest unbalanced node y a right rotation of x about y x x y T 3 T 1 T 2 Note: The pivot of the rotation is the deepest unbalanced node T 2 T 3

Single Left Rotation • Single left rotation: • The right child y of a node x becomes x's parent. • x becomes the left child of y. • The left child T 2 of y, if any, becomes the right child of x. deepest unbalanced node x a left rotation of y about x y T 3 T 1 T 2 T 3 T 1 Note: The pivot of the rotation is the deepest unbalanced node T 2

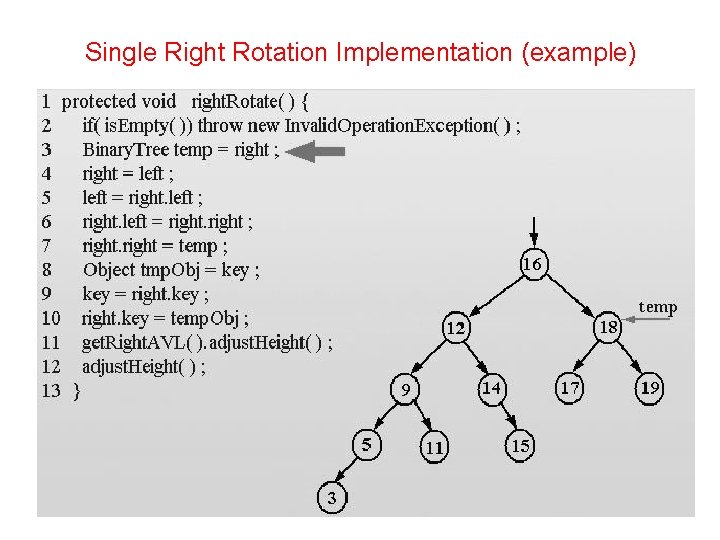
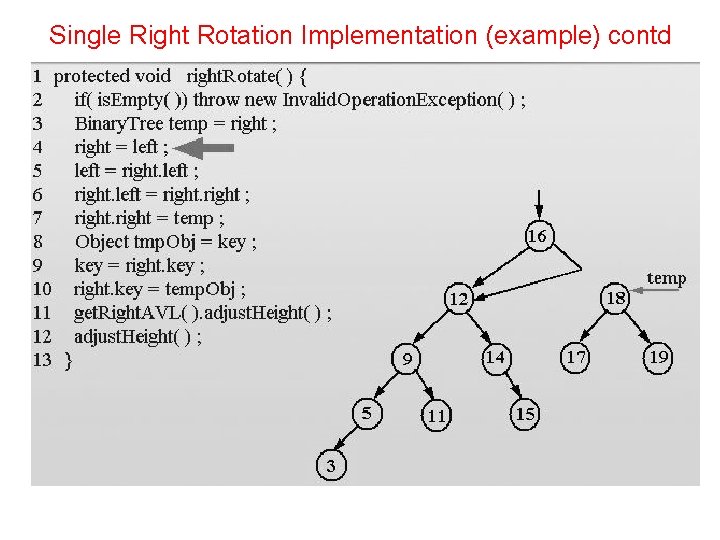
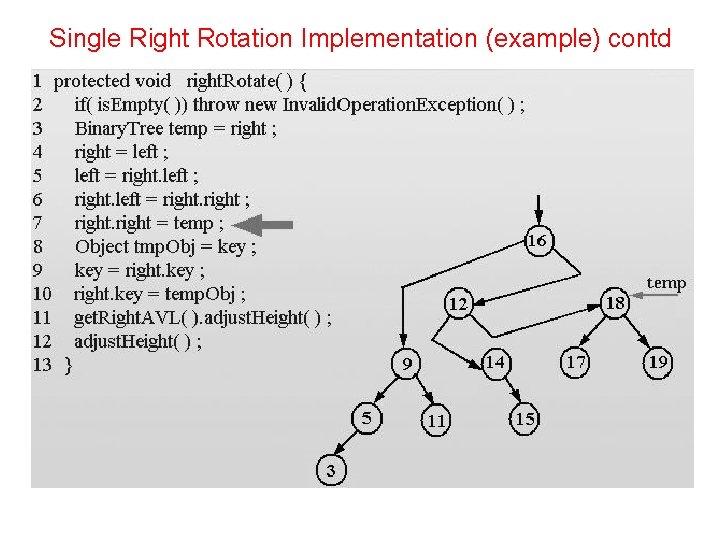
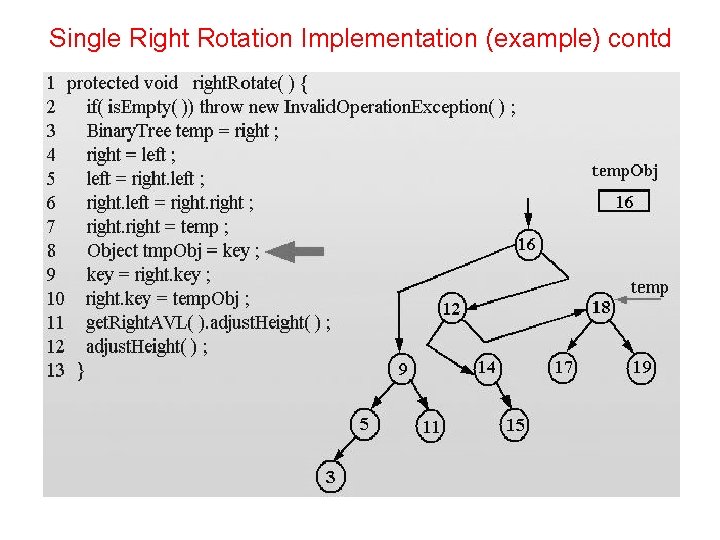
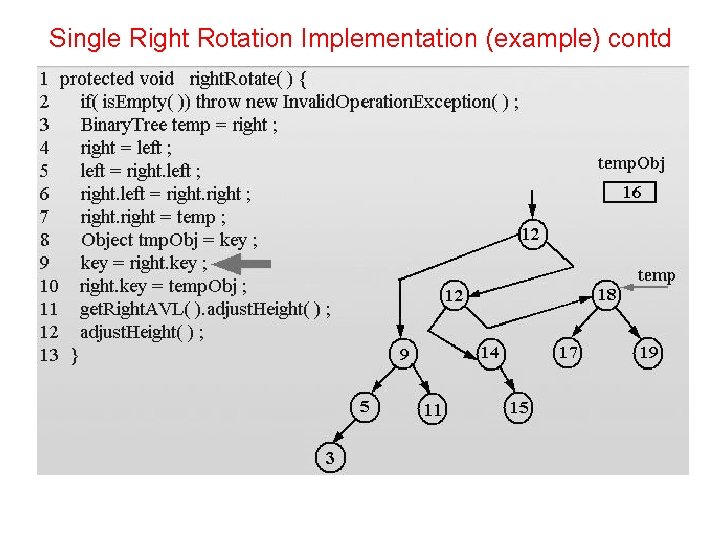
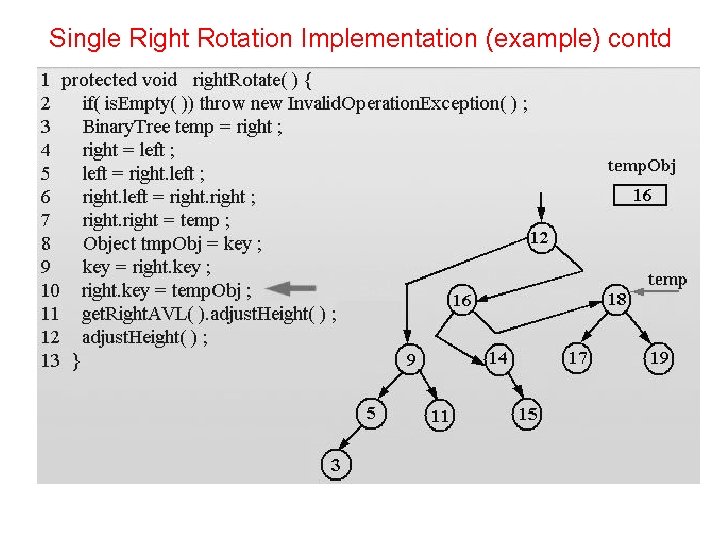
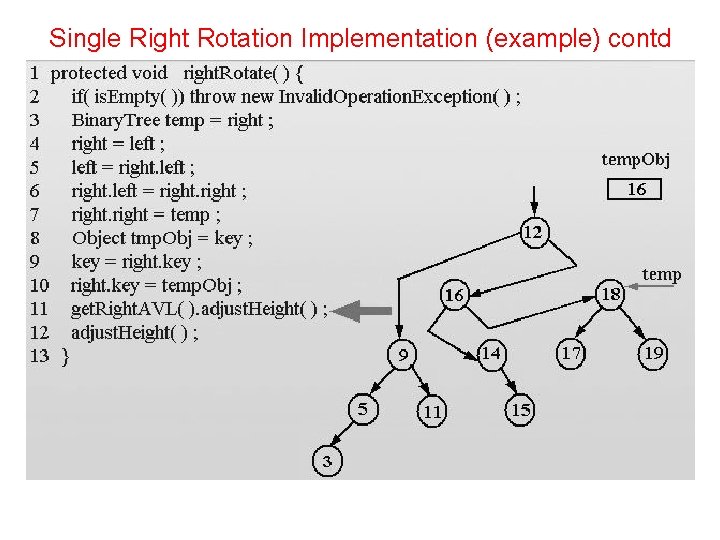
Single Right Rotation Implementation protected void right. Rotate(){ if( is. Empty()) throw new Invalid. Operation. Exception(); Binary. Tree temp = right; right = left; left = right. left; right. left = right; right = temp; Object tmp. Obj = key; key = right. key; right. key = temp. Obj; get. Right. AVL(). adjust. Height(); }

Single Right Rotation Implementation (example)

Single Right Rotation Implementation (example) contd

Single Right Rotation Implementation (example) contd

Single Right Rotation Implementation (example) contd

Single Right Rotation Implementation (example) contd

Single Right Rotation Implementation (example) contd

Single Right Rotation Implementation (example) contd

Single Right Rotation Implementation (example) contd

Single Right Rotation Implementation (example) contd

Single Right Rotation Implementation (example) contd

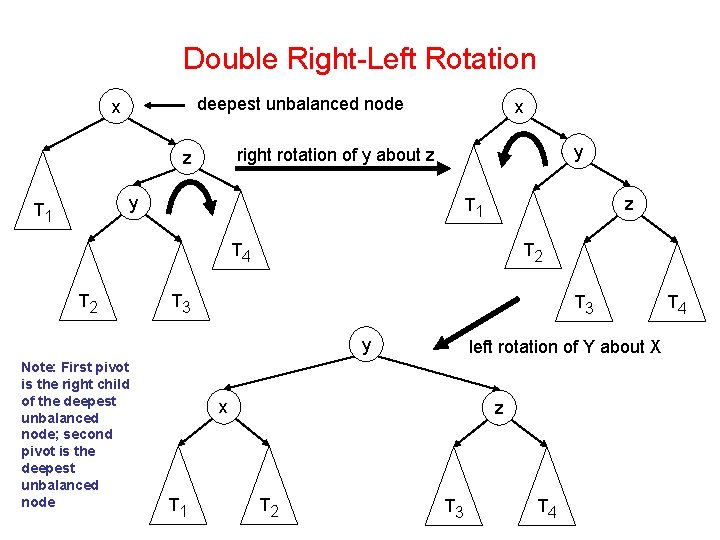
Double Right-Left Rotation deepest unbalanced node x x y right rotation of y about z z y T 1 z T 1 T 2 T 4 T 2 T 3 y Note: First pivot is the right child of the deepest unbalanced node; second pivot is the deepest unbalanced node left rotation of Y about X x T 1 z T 2 T 3 T 4

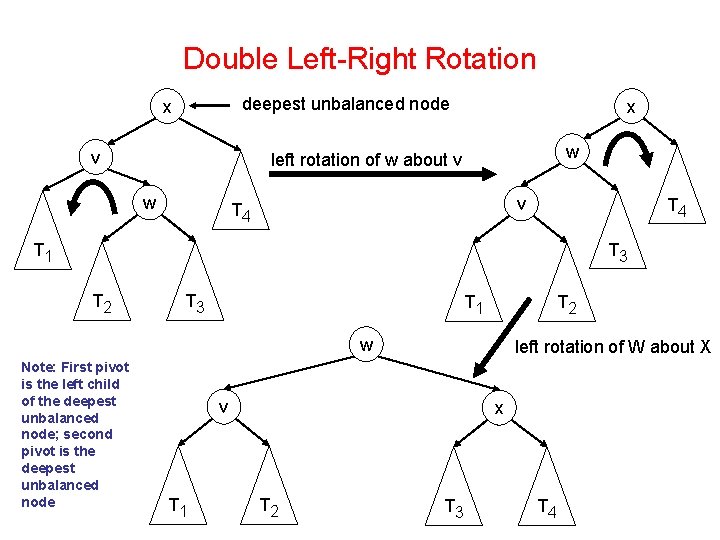
Double Left-Right Rotation deepest unbalanced node x v x w left rotation of w about v w v T 4 T 3 T 1 T 2 w Note: First pivot is the left child of the deepest unbalanced node; second pivot is the deepest unbalanced node left rotation of W about X v T 1 x T 2 T 3 T 4

Double Rotation implementation 1 2 3 4 5 6 7 protected void rotate. Right. Left() { if( is. Empty()) throw new Invalid. Operation. Exception(); get. Right. AVL(). rotate. Right(); rotate. Left(); } 1 2 3 4 5 6 7 protected void rotate. Left. Right() { if( is. Empty()) throw new Invalid. Operation. Exception(); get. Left. AVL(). rotate. Left(); rotate. Right(); }

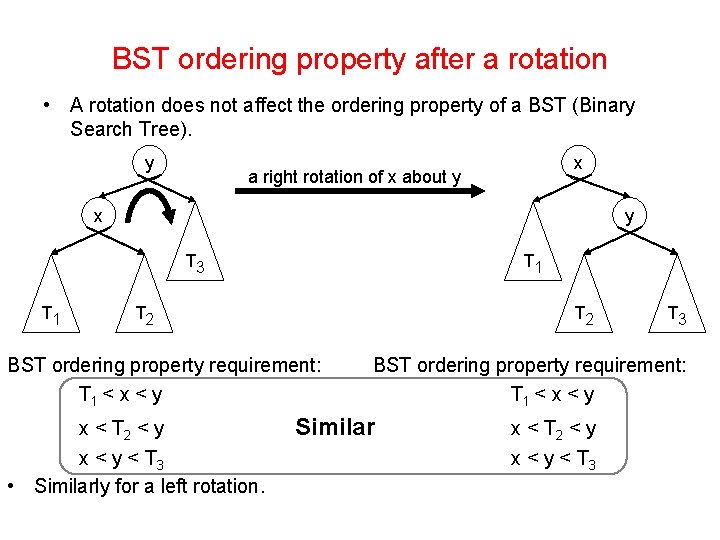
BST ordering property after a rotation • A rotation does not affect the ordering property of a BST (Binary Search Tree). y x a right rotation of x about y x y T 3 T 1 T 2 BST ordering property requirement: T 1 < x < y x < T 2 < y x < y < T 3 • Similarly for a left rotation. T 3 BST ordering property requirement: T 1 < x < y Similar x < T 2 < y x < y < T 3