AVL Trees Balanced Binary Search Trees not covered

AVL Trees Balanced Binary Search Trees (not covered in book, but related to pp 165 -169)

AVL Trees • • First-invented self-balancing binary search tree Named after its two inventors, 1. G. M. Adelson-Velsky and 2. E. M. Landis, – published it in their 1962 paper "An algorithm for the organization of information. "
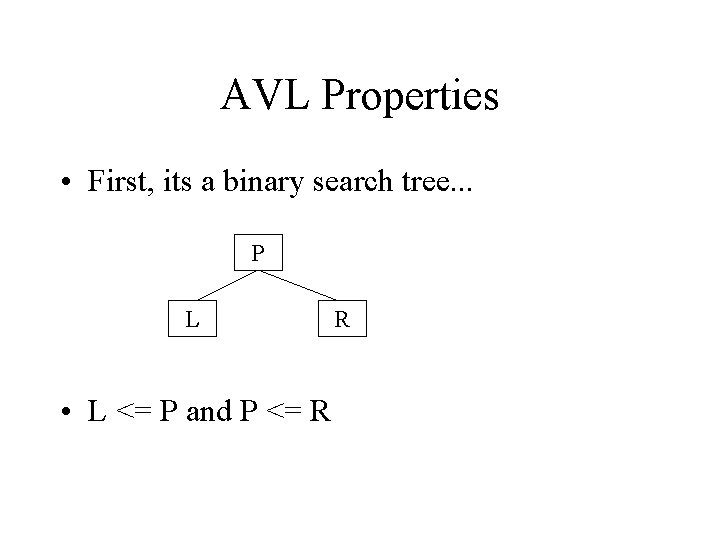
AVL Properties • First, its a binary search tree. . . P L • L <= P and P <= R R

Question? • Is this a binary tree search tree? 50 29 70 12 35 5 3 17 9 15 56 32 21 28 46 34 43 77 53 51 52 60 54 58 71 68 79
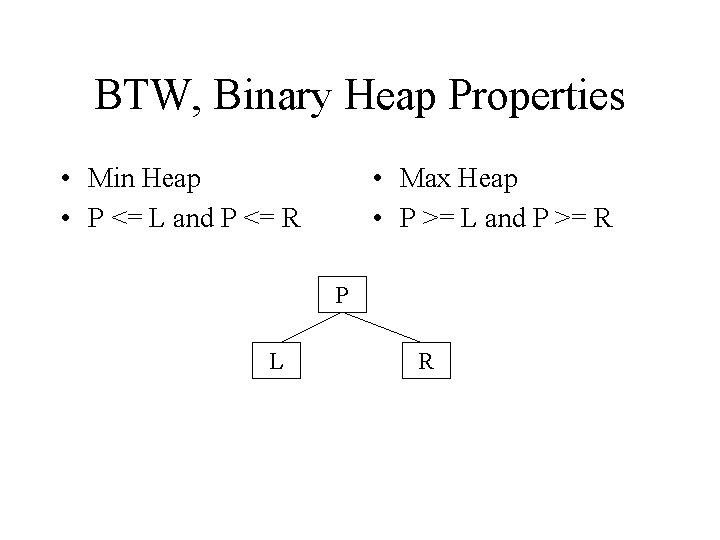
BTW, Binary Heap Properties • Min Heap • P <= L and P <= R • Max Heap • P >= L and P >= R P L R

AVL Properties • An AVL tree is a balanced binary tree • To understand balance we need to understand the notion of Tree Height 55 Height 2 32 71 64 Height 1 86 Height 0

AVL Properties • By default, nodes with no children have a height of Height of 0. 55 Height 0 32 Height 0 64 Height 2 71 Height 1 86 Height 0

AVL Properties • But, we must also understand the concept of Sub-trees Height = max(L. height, R. height) + 1 sub-tree L has a height of 0 55 Height 0 32 Height 0 64 Height 2 71 sub-tree R has a height of 1 Height 1 86 Height 0

AVL Properties • Also empty sub-trees have a Height of -1 Height = max(L. height, R. height) + 1 44 Height = 2 = max(0, 1) + 1 58 Height = 1 = max(-1, 0) + 1 91 Height = 0 = max(-1, -1) + 1

AVL Properties • Anyway, the AVL Balance Property is as follows. . . • For ALL nodes, the Height of the Left and Right Sub-trees can only differ by 1. P L A Node R

AVL Properties • Wouldn’t this be a better Balance property? • For ALL nodes, the Height of the Left and Right Sub-trees must be equal! P L A Node R
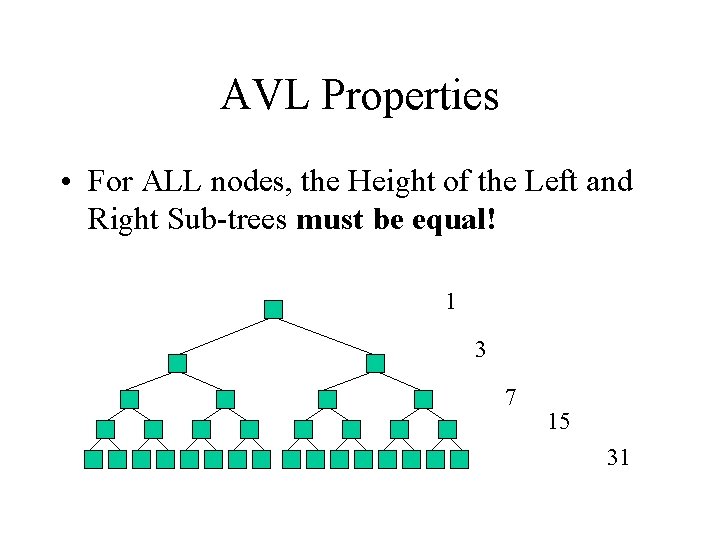
AVL Properties • For ALL nodes, the Height of the Left and Right Sub-trees must be equal! 1 3 7 15 31

AVL Properties • For ALL nodes, the Height of the Left and Right Sub-trees must be equal! • Strict Balance Conditions are too 1 restrictive. 3 7 15 31
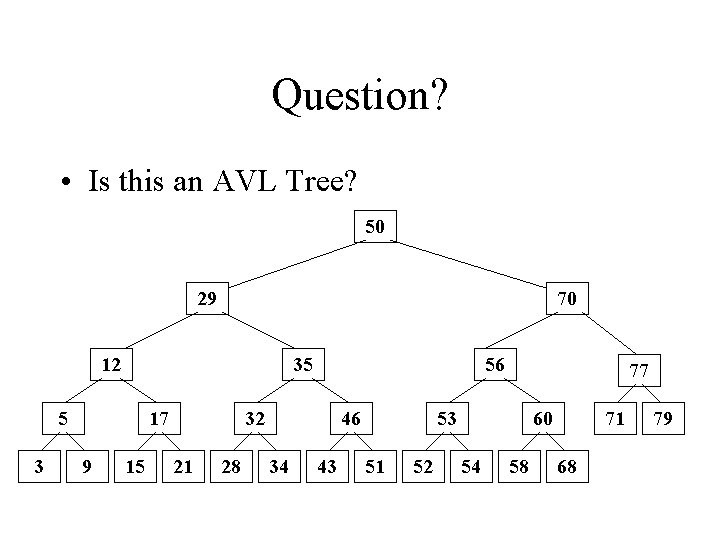
Question? • Is this an AVL Tree? 50 29 70 12 35 5 3 17 9 15 56 32 21 28 46 34 43 77 53 51 52 60 54 58 71 68 79
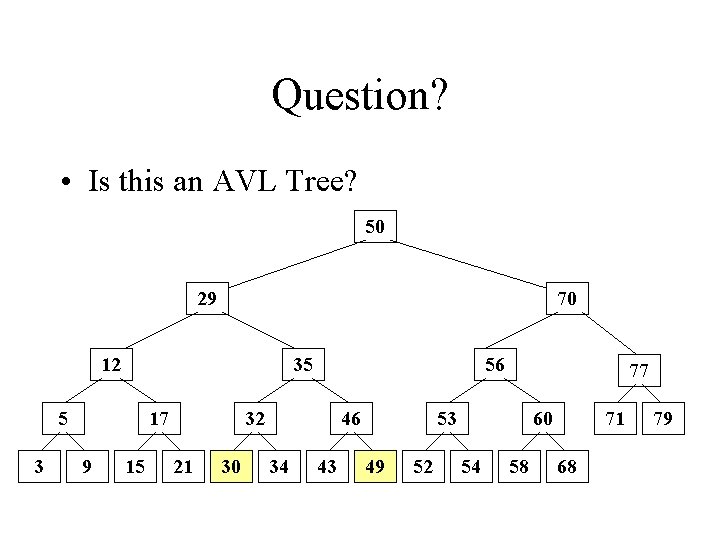
Question? • Is this an AVL Tree? 50 29 70 12 35 5 3 17 9 15 56 32 21 30 46 34 43 77 53 49 52 60 54 58 71 68 79
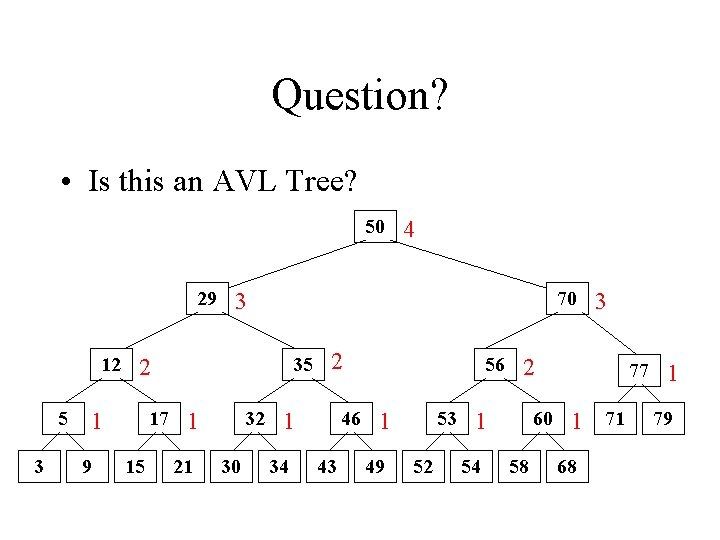
Question? • Is this an AVL Tree? 50 29 12 5 3 9 70 3 35 2 17 1 15 32 1 21 4 30 2 46 1 34 43 56 53 1 49 52 2 60 1 54 3 58 77 1 71 68 1 79
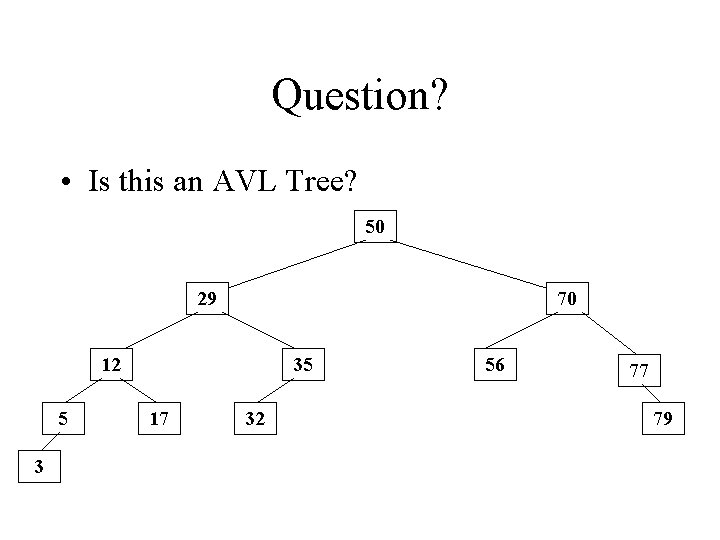
Question? • Is this an AVL Tree? 50 29 70 12 5 3 35 17 32 56 77 79
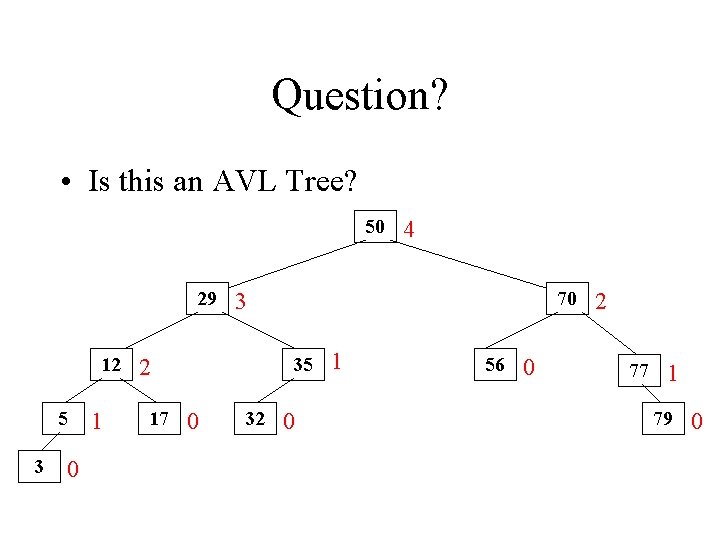
Question? • Is this an AVL Tree? 50 29 12 5 3 0 1 70 3 35 2 17 0 4 32 0 1 56 0 2 77 1 79 0

Question? • Is this an AVL Tree? +1 50 4 +1 29 -1 70 3 +1 12 +1 5 0 3 0 1 +1 2 35 0 17 0 0 32 0 1 0 56 0 2 -1 77 0 1 79 0
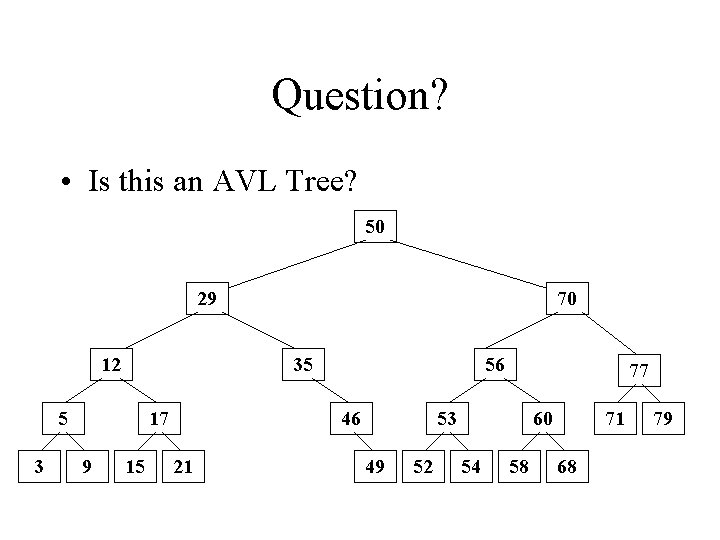
Question? • Is this an AVL Tree? 50 29 12 35 5 3 17 9 70 15 56 46 21 77 53 49 52 60 54 58 71 68 79

Question? • No 50 29 12 35 5 3 17 9 70 15 56 46 21 77 53 49 52 60 54 58 71 68 79
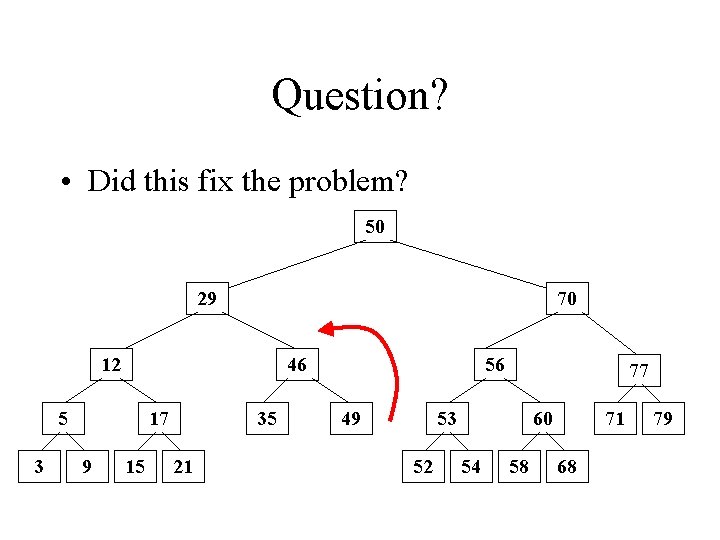
Question? • Did this fix the problem? 50 29 70 12 46 5 3 17 9 15 35 21 56 49 77 53 52 60 54 58 71 68 79
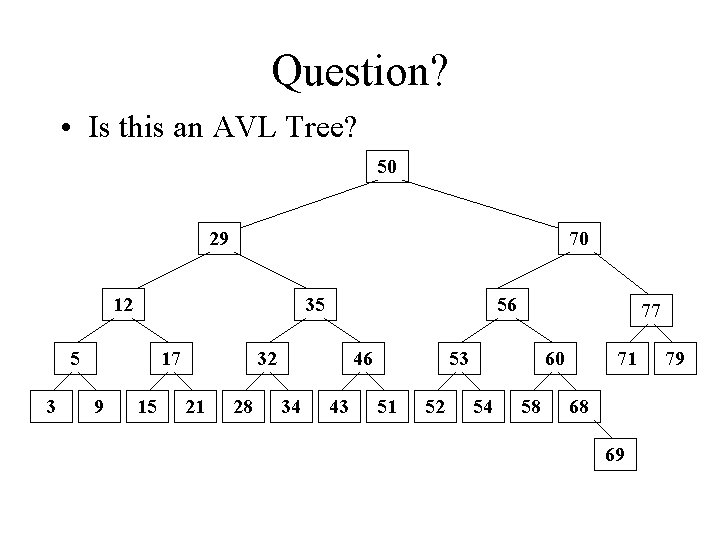
Question? • Is this an AVL Tree? 50 29 70 12 35 5 3 17 9 15 56 32 21 28 46 34 43 77 53 51 52 60 54 58 71 68 69 79
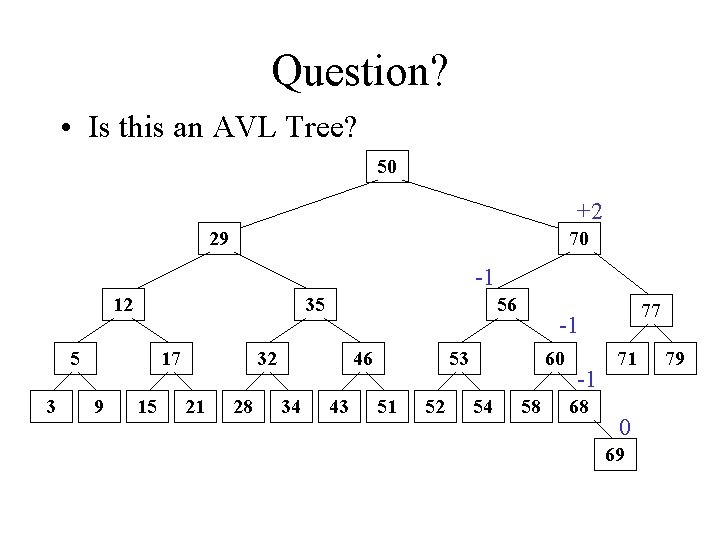
Question? • Is this an AVL Tree? 50 +2 29 70 -1 12 35 5 3 17 9 15 56 32 21 28 46 34 43 -1 53 51 52 60 54 77 58 -1 68 71 0 69 79
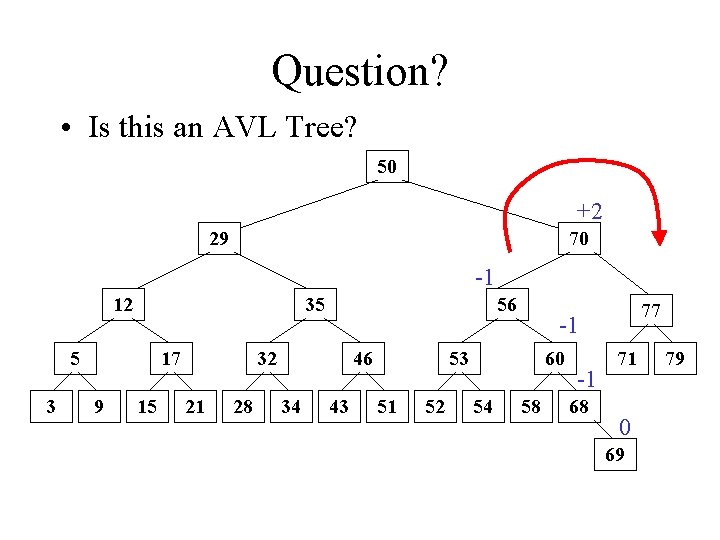
Question? • Is this an AVL Tree? 50 +2 29 70 -1 12 35 5 3 17 9 15 56 32 21 28 46 34 43 -1 53 51 52 60 54 77 58 -1 68 71 0 69 79
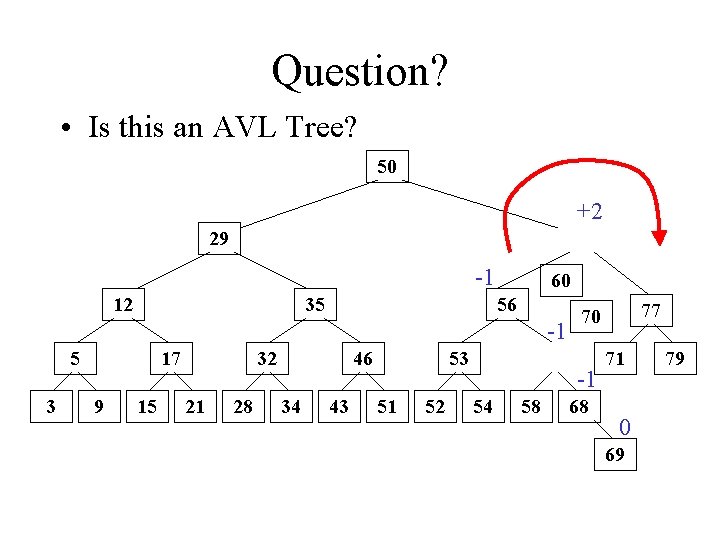
Question? • Is this an AVL Tree? 50 +2 29 -1 12 35 60 56 -1 5 3 17 9 15 32 21 28 46 34 43 53 51 52 -1 54 58 77 70 68 71 0 69 79
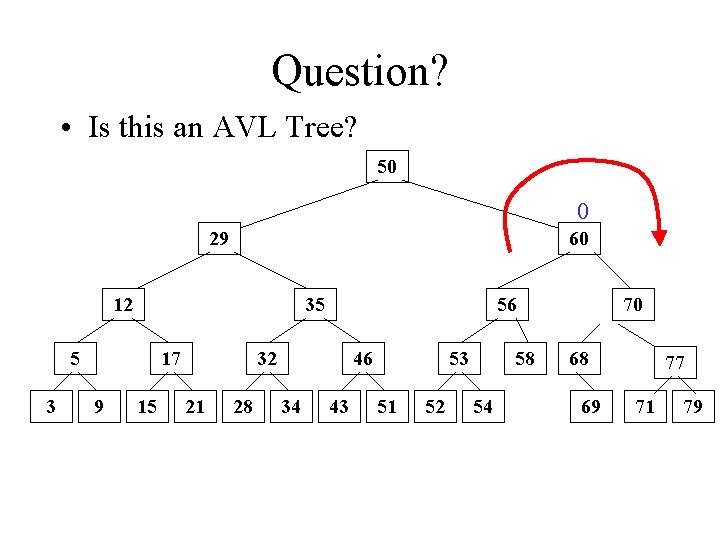
Question? • Is this an AVL Tree? 50 0 29 60 12 35 5 3 17 9 15 56 32 21 28 46 34 43 53 51 52 58 54 70 68 69 77 71 79

Correcting Imbalance 1. After every insertion 2. Check to see if an imbalance was created. • All you have to do backtrack up the tree 3. If you find an imbalance, correct it. 4. As long as the original tree is an AVL tree, there are only 4 types of imbalances that can occur.

Imbalances • • Left-Left (Single Rotation) Right-Right(Single Rotation) Left-Right (Double Rotation) Right-Left(Double Rotation)

Illustration • http: //www. eli. sdsu. edu/courses/fall 96/cs 66 0/notes/avl. html
- Slides: 30