Asymptotic Notation Review of Functions Summations 942021 Asymptotic

Asymptotic Notation, Review of Functions & Summations 9/4/2021

Asymptotic Complexity w Running time of an algorithm as a function of input size n for large n. w Expressed using only the highest-order term in the expression for the exact running time. s 7 n 5 + 2 n 4 + 3 n 3 + 9 n 2 + 4 n + 6 s Instead of exact running time, we use asymptotic notations such as O(n 5), Ω(n), (n 2). w Describes behavior of running time functions by setting lower and upper bounds for their values. asymp - 1

Asymptotic Notation w , O, , o, w Defined for functions over the natural numbers. s Ex: f(n) = (n 2). s Describes how f(n) grows in comparison to n 2. w Define a set of functions; in practice used to compare two function values. w The notations describe different rate-of-growth relations between the defining function and the defined set of functions. asymp - 2

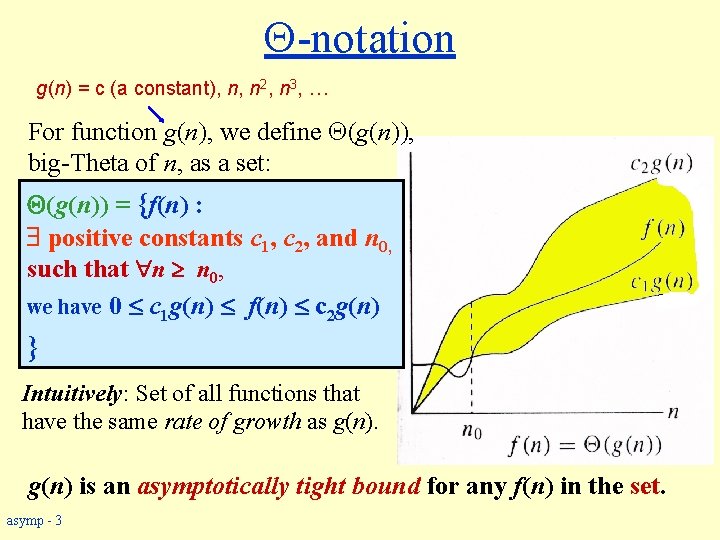
-notation g(n) = c (a constant), n, n 2, n 3, … For function g(n), we define (g(n)), big-Theta of n, as a set: (g(n)) = {f(n) : positive constants c 1, c 2, and n 0, such that n n 0, we have 0 c 1 g(n) f(n) c 2 g(n) } Intuitively: Set of all functions that have the same rate of growth as g(n) is an asymptotically tight bound for any f(n) in the set. asymp - 3

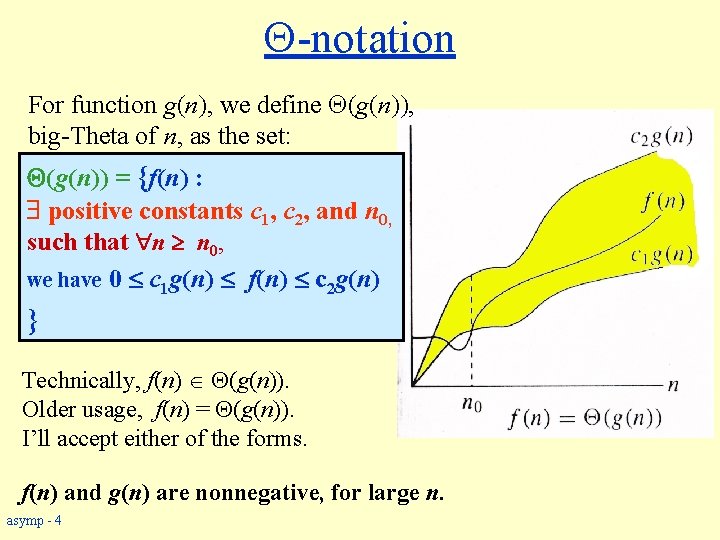
-notation For function g(n), we define (g(n)), big-Theta of n, as the set: (g(n)) = {f(n) : positive constants c 1, c 2, and n 0, such that n n 0, we have 0 c 1 g(n) f(n) c 2 g(n) } Technically, f(n) (g(n)). Older usage, f(n) = (g(n)). I’ll accept either of the forms. f(n) and g(n) are nonnegative, for large n. asymp - 4

Example (g(n)) = {f(n) : positive constants c 1, c 2, and n 0, such that n n 0, 0 c 1 g(n) f(n) c 2 g(n)} w 10 n 2 - 3 n = (n 2)? w What constants for n 0, c 1, and c 2 will work? w Make c 1 a little smaller than the leading coefficient, and c 2 a little bigger. w To compare orders of growth, look at the leading term (highest-order term). w Exercise: Prove that n 2/2 -3 n = (n 2) asymp - 5

Example (g(n)) = {f(n) : positive constants c 1, c 2, and n 0, such that n n 0, 0 c 1 g(n) f(n) c 2 g(n)} • 10 n 2 - 3 n = (n 2)? • To show that this equation holds, we find c 1 = 9, c 2 = 11, and n 0 = 3 and for n ≥ n 0, we always have 9 n 2 ≤ 10 n 2 - 3 n ≤ 11 n 2. asymp - 6

Example (g(n)) = {f(n) : positive constants c 1, c 2, and n 0, such that n n 0, 0 c 1 g(n) f(n) c 2 g(n)} • 10 n 2 - 3 n = (n 2) asymp - 7 • 10 n 2 - 3 n > 9 n 2 >3 ⇒ n 2 > 3 n ⇒ n • 10 n 2 - 3 n < 11 n 2 >-3 ⇒ n 2 > - 3 n ⇒ n

Example (g(n)) = {f(n) : positive constants c 1, c 2, and n 0, such that n n 0, 0 c 1 g(n) f(n) c 2 g(n)} • n 2/2 -3 n = (n 2)? • c 1 = 1/3 ⇒ n 2/2 - 3 n > n 2/3 ⇒ n 2/6 > 3 n ⇒ n > 18 • c 2 = 1 ⇒ n 2/2 - 3 n < n 2 ⇒ n 2 > - 6 n ⇒ n > - 6 • Then, for n > n 0 = 18, we will definitely have n 2/3 < n 2/2 - 3 n < n 2. asymp - 8

Example (g(n)) = {f(n) : positive constants c 1, c 2, and n 0, such that n n 0, 0 c 1 g(n) f(n) c 2 g(n)} w Is 3 n 3 (n 4)? w How about 22 n (2 n)? asymp - 9

Example (g(n)) = {f(n) : positive constants c 1, c 2, and n 0, such that n n 0, 0 c 1 g(n) f(n) c 2 g(n)} • Is 3 n 3 (n 4)? • If it is true, we can find c 1, c 2, and n 0 such that for n > n 0, we have c 1 n 4 ≤ 3 n 3 ≤ c 2 n 4. c 1 n 4 ≤ 3 n 3 ⇒ n ≤ 3/c 1. • It is a contradiction. So, 3 n 3 (n 4)? asymp - 10

Example (g(n)) = {f(n) : positive constants c 1, c 2, and n 0, such that n n 0, 0 c 1 g(n) f(n) c 2 g(n)} • How about 22 n (2 n)? • If it is true, we can find c 1, c 2, and n 0 such that for n > n 0, we have c 12 n ≤ 22 n ≤ c 22 n ⇒ 2 n ≤ c 2 ⇒ n ≤ log 2 c 2. • It is a contradiction. So, 22 n (2 n)? asymp - 11

O-notation For function g(n), we define O(g(n)), big-O of n, as the set: O(g(n)) = {f(n) : positive constants c and n 0, such that n n 0, we have 0 f(n) cg(n) } Intuitively: Set of all functions whose rate of growth is the same as or lower than that of g(n) is an asymptotic upper bound for any f(n) in the set. f(n) = (g(n)) f(n) = O(g(n)). (g(n)) O(g(n)). asymp - 12

Examples O(g(n)) = {f(n) : positive constants c and n 0, such that n n 0, we have 0 f(n) cg(n) } w Any linear function an + b is in O(n 2). How? w Show that 3 n 3 = O(n 4) for appropriate c and n 0. w Show that 3 n 3 = O(n 3) for appropriate c and n 0. asymp - 13

Examples . O(g(n)) = {f(n) : positive constants c and n 0, such that n n 0, we have 0 f(n) cg(n) } w asymp - 14

Examples O(g(n)) = {f(n) : positive constants c and n 0, such that n n 0, we have 0 f(n) cg(n) } • Show that 3 n 3 = O(n 4) for appropriate c and n 0. • The answer is obviously yes, since for any n > n 0 = 4, we must have n 4 > 3 n 3. • Show that 3 n 3 = O(n 3) for appropriate c and n 0. • The answer is also yes, since we can take c = 4, and for any n > n 0 = 1, we must have cn 3 > 3 n 3. asymp - 15

-notation For function g(n), we define (g(n)), big-Omega of n, as the set: (g(n)) = {f(n) : positive constants c and n 0, such that n n 0, we have 0 cg(n) f(n)} Intuitively: Set of all functions whose rate of growth is the same as or higher than that of g(n) is an asymptotic lower bound for any f(n) in the set. f(n) = (g(n)). asymp - 16

Example w (g(n)) = {f(n) : positive constants c and n 0, such that n n 0, we have 0 cg(n) f(n)} asymp - 17

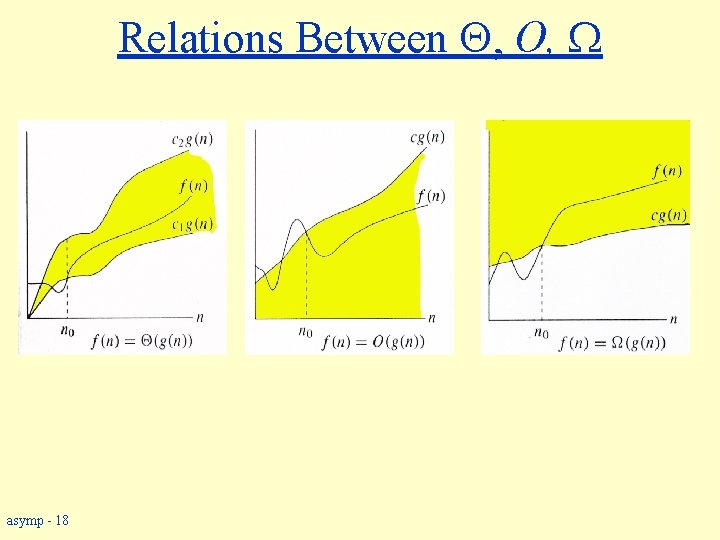
Relations Between , O, asymp - 18

Relations Between , , O Theorem : For any two functions g(n) and f(n), f(n) = (g(n)) iff f(n) = O(g(n)) and f(n) = (g(n)). w That is, (g(n)) = O(g(n)) Ç (g(n)) w In practice, asymptotically tight bounds are obtained from asymptotic upper and lower bounds. asymp - 19

Running Times w “Running time is O(f(n))” Worst case is O(f(n)) w O(f(n)) bound on the worst-case running time O(f(n)) bound on the running time of every input. w (f(n)) bound on the worst-case running time (f(n)) bound on the running time of every input. w “Running time is (f(n))” Best case is (f(n)) w Can still say “Worst-case running time is (f(n))” s Means worst-case running time is given by some unspecified function g(n) (f(n)). asymp - 20

Example w Insertion sort takes (n 2) in the worst case, so sorting (as a problem) is O(n 2). Why? w Any sort algorithm must look at each item, so sorting is (n). w In fact, using (e. g. ) merge sort, sorting is (n lg n) in the worst case. s Later, we will prove that we cannot hope that any comparison sort to do better in the worst case. asymp - 21

Asymptotic Notation in Equations w Can use asymptotic notation in equations to replace expressions containing lower-order terms. w For example, 4 n 3 + 3 n 2 + 2 n + 1 = 4 n 3 + 3 n 2 + (n) = 4 n 3 + (n 2) = (n 3). How to interpret? w In equations, (f(n)) always stands for an anonymous function g(n) (f(n)) s In the example above, (n 2) stands for 3 n 2 + 2 n + 1. asymp - 22

o-notation For a given function g(n), the set little-o: o(g(n)) = {f(n): c > 0, n 0 > 0 such that n n 0, we have 0 f(n) < cg(n)}. w asymp - 23

little-o: o(g(n)) = {f(n): c > 0, n 0 > 0 such that n n 0, we have 0 f(n) < cg(n)}. big-O: O(g(n)) = {f(n) : positive constants c and n 0, such that n n 0, we have 0 f(n) cg(n) } asymp - 24

-notation For a given function g(n), the set little-omega: (g(n)) = {f(n): c > 0, n 0 > 0 such that n n 0, we have 0 cg(n) < f(n)}. w asymp - 25

little- : (g(n)) = {f(n): c > 0, n 0 > 0 such that n n 0, we have 0 cg(n) < f(n)}. big- : (g(n)) = {f(n) : positive constants c and n 0, such that n n 0, we have 0 cg(n) f(n)} asymp - 26

Comparison of Functions f g a b f (n) = O(g(n)) a b f (n) = (g(n)) a = b f (n) = o(g(n)) a < b f (n) = (g(n)) a > b asymp - 27

Limits w nlim [f(n) / g(n)] = 0 f(n) o(g(n)) w nlim [f(n) / g(n)] < f(n) O(g(n)) w 0 < nlim [f(n) / g(n)] < f(n) (g(n)) w 0 < nlim [f(n) / g(n)] f(n) (g(n)) w nlim [f(n) / g(n)] = f(n) (g(n)) w nlim [f(n) / g(n)] undefined can’t say asymp - 28

Properties w Transitivity f(n) = (g(n)) & g(n) = (h(n)) f(n) = (h(n)) f(n) = O(g(n)) & g(n) = O(h(n)) f(n) = O(h(n)) f(n) = (g(n)) & g(n) = (h(n)) f(n) = (h(n)) f(n) = o (g(n)) & g(n) = o (h(n)) f(n) = o (h(n)) f(n) = (g(n)) & g(n) = (h(n)) f(n) = (h(n)) w Reflexivity f(n) = (f(n)) f(n) = O(f(n)) f(n) = (f(n)) asymp - 29

Properties w Symmetry f(n) = (g(n)) iff g(n) = (f(n)) w Complementarity f(n) = O(g(n)) iff g(n) = (f(n)) f(n) = o(g(n)) iff g(n) = ((f(n)) asymp - 30

Common Functions 9/4/2021

Monotonicity w f(n) is s s asymp - 32 monotonically increasing if m n f(m) f(n). monotonically decreasing if m n f(m) f(n). strictly increasing if m < n f(m) < f(n). strictly decreasing if m > n f(m) > f(n).

Exponentials w Useful Identities: w Exponentials and polynomials asymp - 33

Logarithms x = logba is the exponent for a = bx. Natural log: ln a = logea Binary log: lg a = log 2 a lg 2 a = (lg a)2 lg lg a = lg (lg a) asymp - 34

Logarithms and exponentials – Bases w If the base of a logarithm is changed from one constant to another, the value is altered by a constant factor. s Ex: log 10 n * log 210 = log 2 n. s Base of logarithm is not an issue in asymptotic notation. w Exponentials with different bases differ by a exponential factor (not a constant factor). s Ex: 2 n = (2/3)n*3 n. asymp - 35

Polylogarithms w For a 0, b > 0, lim n ( lga n / nb ) = 0, so lga n = o(nb), and nb = (lga n ) s Prove using L’Hopital’s rule repeatedly w lg(n!) = (n lg n) s Prove using Stirling’s approximation (in the text) for lg(n!). asymp - 36

Exercise Express functions in A in asymptotic notation using functions in B. A 5 n 2 + 100 n B 3 n 2 + 2 A (B) A (n 2), n 2 (B) A (B) log 3(n 2) log 2(n 3) A (B) logba = logca / logcb; A = 2 lgn / lg 3, B = 3 lgn, A/B =2/(3 lg 3) A (B) nlg 4 3 lg n alog b = blog a; B =3 lg n=nlg 3; A/B =nlg(4/3) as n A o (B) lg 2 n n 1/2 lim ( lga n / nb ) = 0 (here a = 2 and b = 1/2) A o (B) n asymp - 37

Summations – Review 9/4/2021

Review on Summations w Why do we need summation formulas? For computing the running times of iterative constructs (loops). (CLRS – Appendix A) Example: Maximum Subvector Given an array A[1…n] of numeric values (can be positive, zero, and negative) determine the subvector A[i…j] (1 i j n) whose sum of elements is maximum over all subvectors. 1 asymp - 39 -2 2 2

Review on Summations Max. Subvector(A, n) maxsum ¬ 0; for i ¬ 1 to n do for j = i to n sum ¬ 0 for k ¬ i to j do sum += A[k] maxsum ¬ max(sum, maxsum) return maxsum n n j w. T(n) = 1 i=1 j=i k=i w. NOTE: This is not a simplified solution. What is the final answer? asymp - 40

Review on Summations w Constant Series: For integers a and b, a b, w Linear Series (Arithmetic Series): For n 0, w Quadratic Series: For n 0, asymp - 41

Review on Summations w Cubic Series: For n 0, w Geometric Series: For real x 1, For |x| < 1, asymp - 42

Review on Summations w Linear-Geometric Series: For n 0, real c 1, w Harmonic Series: nth harmonic number, n I+, asymp - 43

Review on Summations w Telescoping Series: w Differentiating Series: For |x| < 1, asymp - 44

Review on Summations w Approximation by integrals: s For monotonically increasing f(n) s For monotonically decreasing f(n) w How? asymp - 45

Review on Summations w nth harmonic number asymp - 46

Reading Assignment w Chapter 4 of CLRS. asymp - 47