Animcie a striedanie snmkov spajte pkami Vyuvajte nvrat

Animácie a striedanie snímkov spúšťajte šípkami. Využívajte návrat do MENU

MENU STOP Titulok koniec prezentácie Základné informácie o vektoroch 1 Násobenie vektora číslom (skalárom) Základné informácie o vektoroch 2 Násobenie vektora číslom - ilustrácia Kolineárne a komplanárne vektory Jednotkový vektor Súčet vektorov Príklad - dôkaz Operácie s vektormi Rozklad vektora na zložky Rozdiel vektorov Lineárna kommbinácia vektorov Príklad na súčet a rozdiel Skalárny súčin vektorov Ilustrácia súčtu vektorov Vektorový súčin vektorov

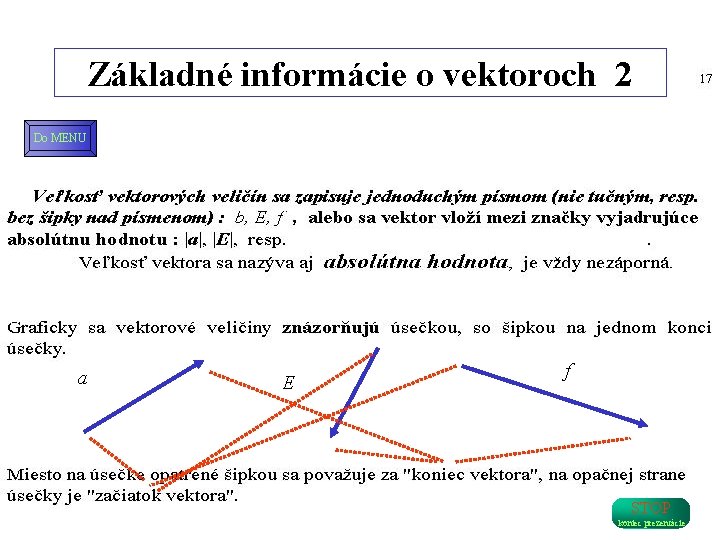
Základné informácie o vektoroch 1 Do MENU STOP koniec prezentácie [1 [1]1] Presná definícia vektorov v trojrozmernom priestore hovorí o trojiciach čísel, ktoré sa predpísaným spôsobom transformujú pri otočení súradnicovej sústavy.

Základné informácie o vektoroch 2 Do MENU a E f STOP koniec prezentácie

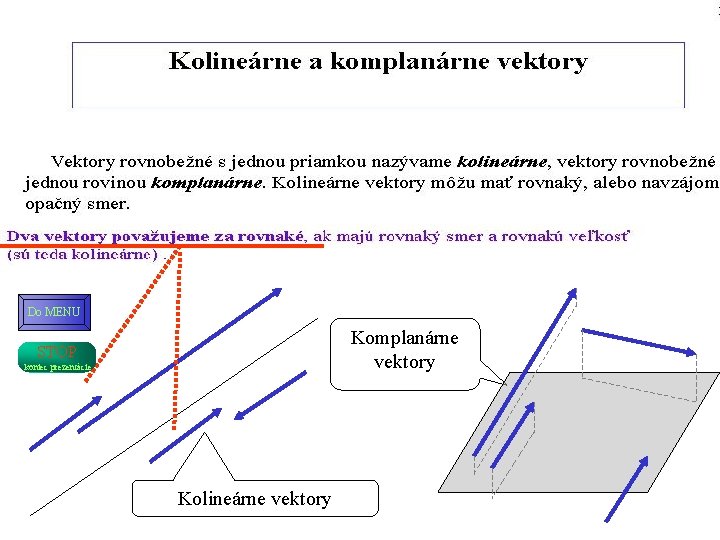
Do MENU Komplanárne vektory STOP koniec prezentácie Kolineárne vektory

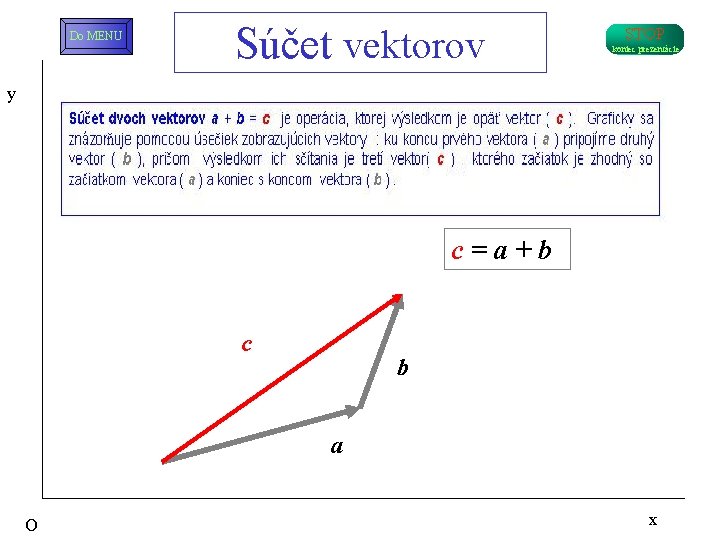
Do MENU Súčet vektorov STOP koniec prezentácie y c = a + b c b a O x

Operácie s vektormi Do MENU STOP koniec prezentácie b = -a a -a b

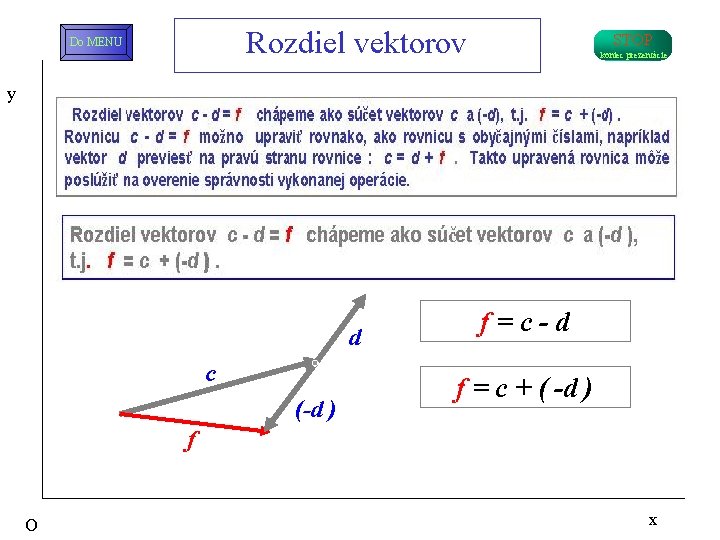
Rozdiel vektorov Do MENU STOP koniec prezentácie y d c (-d ) f = c - d f = c + ( -d ) f O x

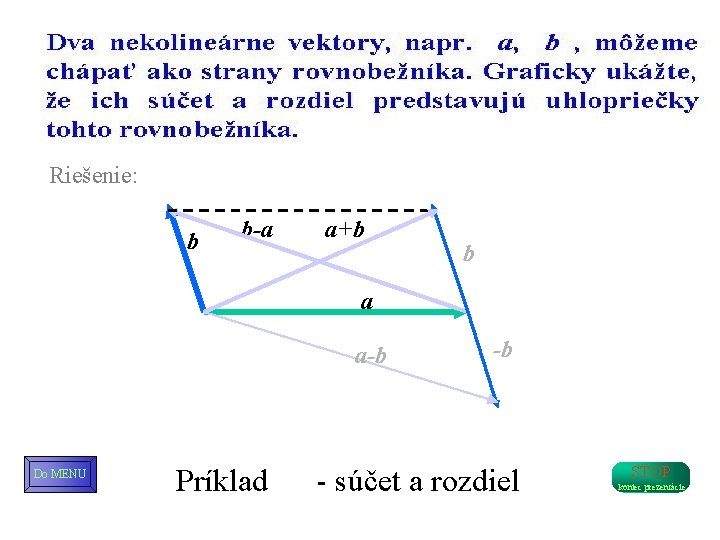
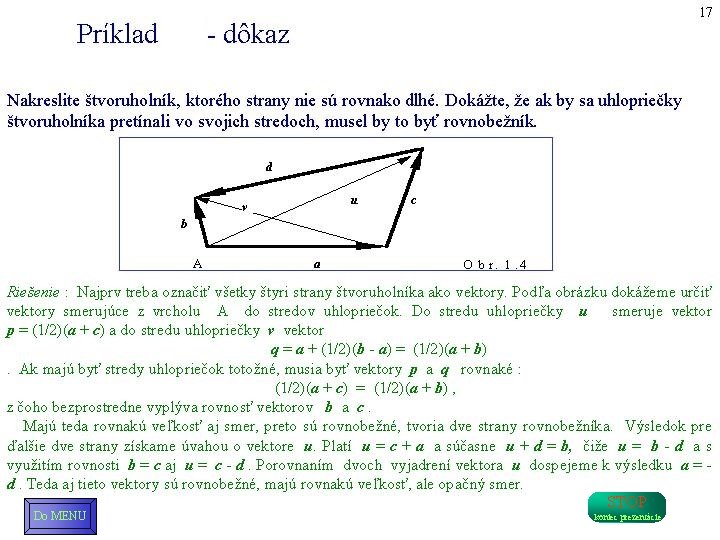
Riešenie: b b-a a+b b a a-b Do MENU -b Príklad 1. 1 - súčet a rozdiel STOP koniec prezentácie

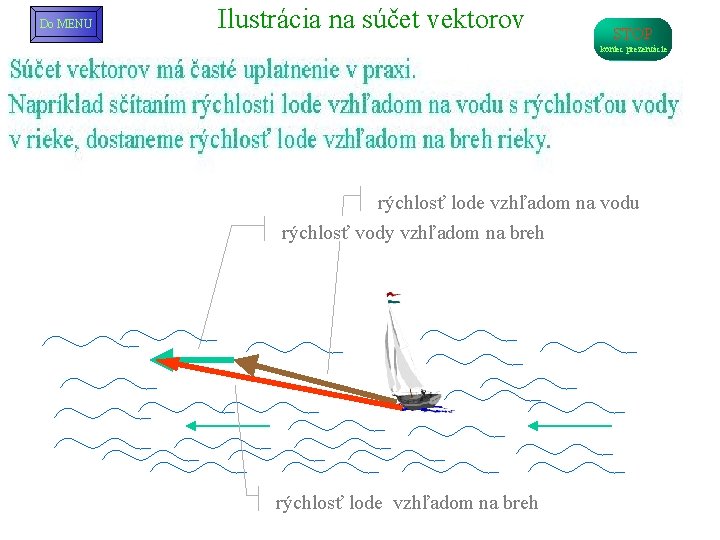
Do MENU Príklad 1. 1 - ilustrácia Ilustrácia na súčet vektorov STOP koniec prezentácie rýchlosť lode vzhľadom na vodu rýchlosť vody vzhľadom na breh rýchlosť lode vzhľadom na breh

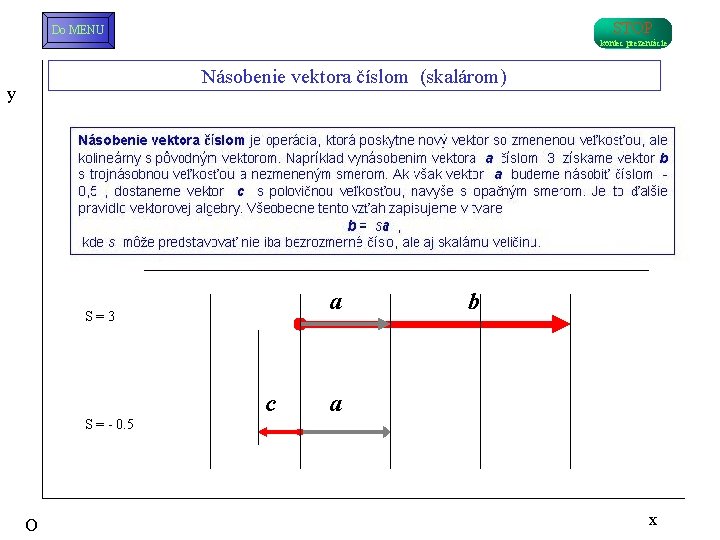
STOP Do MENU koniec prezentácie Násobenie vektora číslom (skalárom) y S = 3 S = - 0. 5 O a c b a x

Násobenie vektora číslom - ilustrácia Do MENU STOP koniec prezentácie

Do MENU STOP koniec prezentácie

Do MENU STOP koniec prezentácie

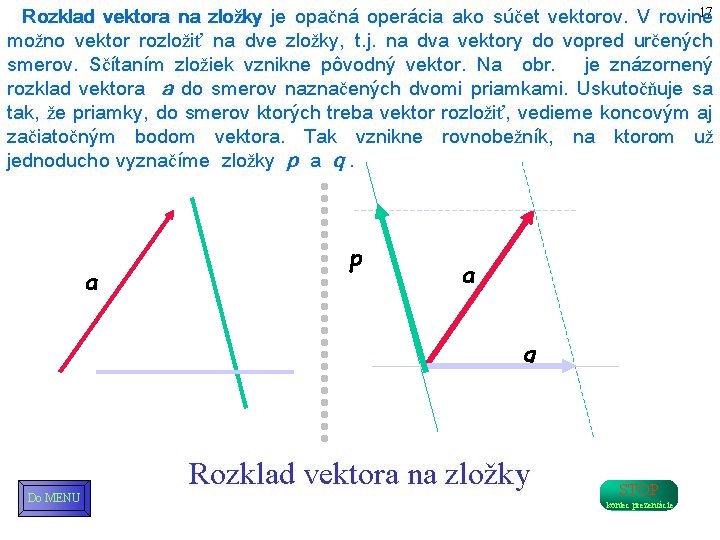
a p a q Do MENU STOP koniec prezentácie

Do MENU Lineárna kombinácia vektorov V priamkach, do ktorých rozkladáme vektor a , môžeme zvoliť jednotkové vektory, ktoré označíme e 1 a e 2. Jednotkovými vektormi sú potom určené smery rozkladania. Zložky p a q možno vyjadriť ako skalárne násobky vektorov e 1 a e 2 : p = ape 1 , q = aqe 2. Vektor e 1 však môže mať opačný smer ako zložka p , a vtedy skalár ap pred vektorom e 1 musí byť záporný. Preto skalár ap nepredstavuje veľkosť vektora p, ale je jednou zo súradníc rozloženého vektora a vo vzťažnej sústave určenej vektormi e 1 a e 2. Vektor a možno po takomto rozklade na zložky vyjadriť v tvare a = p + q = a p e 1 + a qe 2. O takomto vyjadrení hovoríme, že vektor a je lineárnou kombináciou vektorov e 1 a e 2. STOP koniec prezentácie

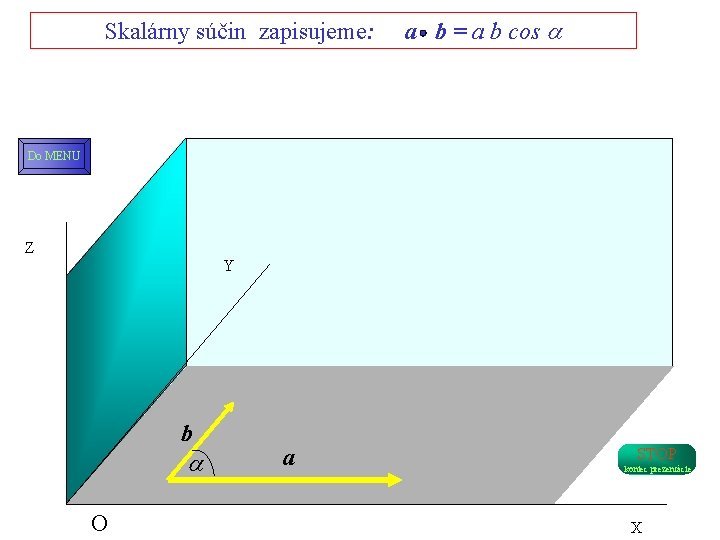
Do MENU Skalárny súčin dvoch vektorov STOP koniec prezentácie Skalárny súčin dvoch vektorov je zavedený ako operácia, ktorej výsledkom je skalárna veličina. Veľkosť tejto skalárnej veličiny je určená súčinom veľkostí príslušných vektorov a kosínusu uhla, ktorý tieto vektory zvierajú. Fyzikálny rozmer výslednej skalárnej veličiny sa rovná súčinu rozmerov násobených vektorových veličín. Skalárny súčin sa označuje bodkou medzi vektormi, v strede výšky písmen, nie na úrovni riadku a b = ab cos Pritom uhol medzi dvoma vektormi sa určuje tak, aby nebol väčší ako radiánov (180 o). Bezpečne ho určíme tak, keď oba vektory nakreslíme zo spoločným začiatkom.

Skalárny súčin zapisujeme: a b = a b cos Do MENU Z Y b O a STOP koniec prezentácie X

Do MENU Skalárny súčin sa často využiva v mechanike, alebo teórii elektromagnetického poľa. Napríklad skalárnym súčinom vektora sily f a vektora elementárneho posunutia dr sa vyjadruje elementárna práca d. A = f dr = f dr cos , lebo smer sily a smer posunutia telesa nemusia byť rovnaké. Vtedy sa na vykonanie práce využíva iba priemet sily do smeru posunutia, vyjadrený ako f cos . Fyzikálny rozmer skalárneho súčinu bude rovnaký ako pre prácu. dr dr cos f STOP koniec prezentácie

Do MENU Vektorový súčin dvoch vektorov STOP koniec prezentácie Vektorový súčin dvoch vektorov je operácia, ktorej výsledkom je vektor. Preto treba definovať nie iba veľkosť výsledku, ale aj smer výsledného vektora. Vektorový súčin sa označuje krížikom medzi vektormi : c = a b Veľkosť c výsledného vektora c je definovaná ako súčin veľkostí násobených vektorov a sínusu uhla nimi zovretého : c = ab sin Pre smer vektora c platí definícia, že je kolmý na rovinu násobených vektorov. Jednoznačnosť definície však vyžaduje určiť, na ktorú stranu roviny smeruje. Vektor c má taký smer, že z jeho konca sa stotožnenie prvého vektora zo súčinu (v tomto prípade vektora a) s druhým vektorom po kratšom oblúku javí ako pohyb proti chodu hodinových ručičiek. O trojici vektorov a, b, c v danom poradí potom hovoríme, že tvoria pravotočivú sústavu vektorov. Zmena ich poradia jednou permutáciou znamená zmenu z pravotočivej na ľavotočivú sústavu (trojicu).

Na obrázku je trojica vektorov a, b, c znázornená v axonometrickom pohľade. Pre názornosť sú nakreslené aj súradnicové osi karteziánskej sústavy. Ak otáčanie vektora a k vektoru b po kratšom oblúku napodobíme otáčaním pravotočivej skrutky, umiestnenej v začiatku súradnicovej sústavy kolmo na rovinu vektorov a b , skrutka sa bude posúvať v smere vektora c. Aj tento model pomáha pri určovaní smeru vektora, ktorý je výsledkom vektorového súčinu. Do MENU zapisujeme: c = a x b b a c d POZOR : d = b x a b O a STOP koniec prezentácie X

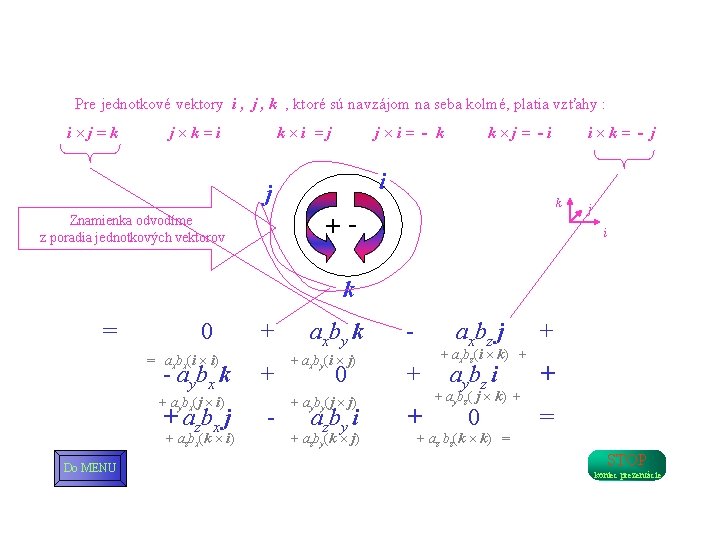
STOP Do MENU koniec prezentácie Na základe distributívneho zákona vektorový súčin vektorov vyjadrených v zložkovom tvare môžeme vyjadriť nasledovne : a b = (ax i + ay j + az k) (bx i + by j + bz k ) = 0 = axbx(i i) + axby(i j) + axbz(i k) + + aybx(j i) + ayby 0(j j) + a b ( j k) + y z + azbx(k i) + azby(k j) + az bz(k k) = 0 i i = 0 j x j = 0 k k = 0

Pre jednotkové vektory i , j , ktoré sú navzájom na seba kolmé, platia vzťahy : i j = k j k = i k i = j j i = - k k j = - i k = - j i j Znamienka odvodíme z poradia jednotkových vektorov k +- j i k = 0 + axby k - axbz j + = axbx(i i) + axby(i j) + axbz(i k) + - aybx k + 0 + aybz i + + aybx(j i) + ayby(j j) + aybz( j k) + + azbx j - azby i + 0 = + azbx(k i) Do MENU + azby(k j) + az bz(k k) = STOP koniec prezentácie

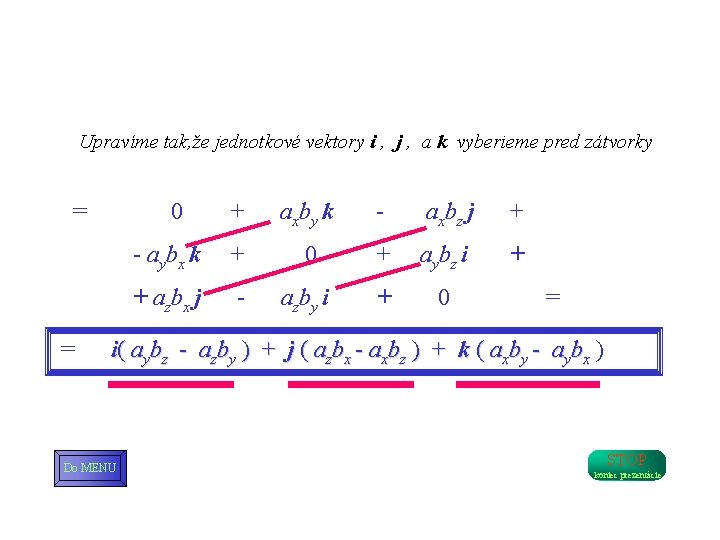
Upravíme tak, že jednotkové vektory i , j , a k vyberieme pred zátvorky = 0 + axby k - axbz j + - aybx k + 0 + aybz i + + azbx j - azby i + 0 = = i( aybz - azby ) + j ( azbx - axbz ) + k ( axby - aybx ) Do MENU STOP koniec prezentácie

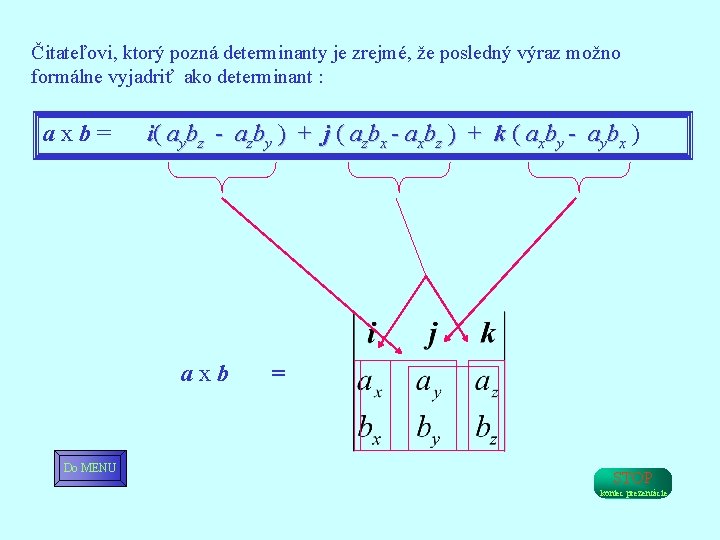
Čitateľovi, ktorý pozná determinanty je zrejmé, že posledný výraz možno formálne vyjadriť ako determinant : a x b = i( aybz - azby ) + j ( azbx - axbz ) + k ( axby - aybx ) a x b = Do MENU STOP koniec prezentácie

Koniec prezentácie VEKTORY Do MENU STOP koniec prezentácie