Alan Turing WWII codebreaker mathematical proof of Turing

Alan Turing • • • WWII code-breaker mathematical proof of ‘Turing machines’ …in particular, “Universal Turing machine” laid foundations of computer science father of artificial intelligence

Parts of a Turing machine § 1. the ‘tape’ § stores symbols § divided into ‘squares’ § 2. the read/write head (i. e. ‘machine head’) § can read/write symbols on tape § 3. finite set of internal states q 0, …, qn § 4. finite alphabet of symbols b 1, …, bm § 5. Machine table (instructions for machine)

Basic example: add-two-numbers machine § alphabet of symbols: • “#” = scratch symbol • “ 1” = tally mark • “+” = addition symbol § internal states of machine: • q 0 • q 1 § tape: # § read-write head: # 1 q 0 1 1 + 1 1 # #

Basic example: add-two-numbers machine # # 1 1 1 + 1 1 # # # q 0 # # 1 q 1
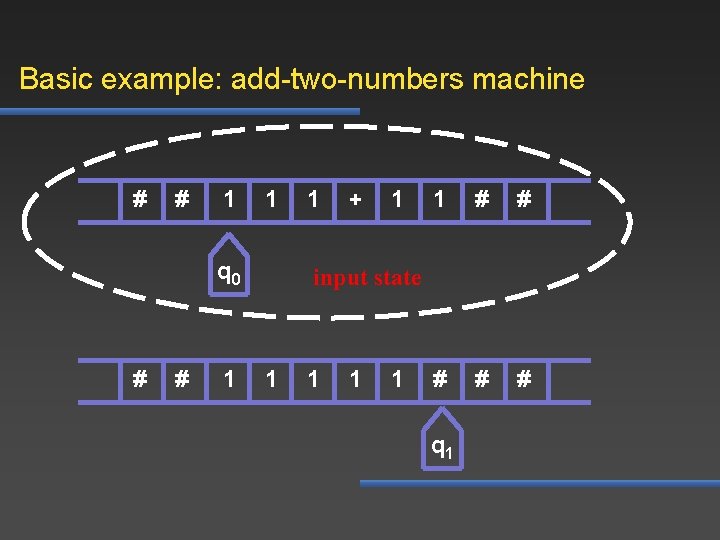
Basic example: add-two-numbers machine # # 1 1 q 0 # # 1 1 + 1 1 # # # input state 1 1 q 1
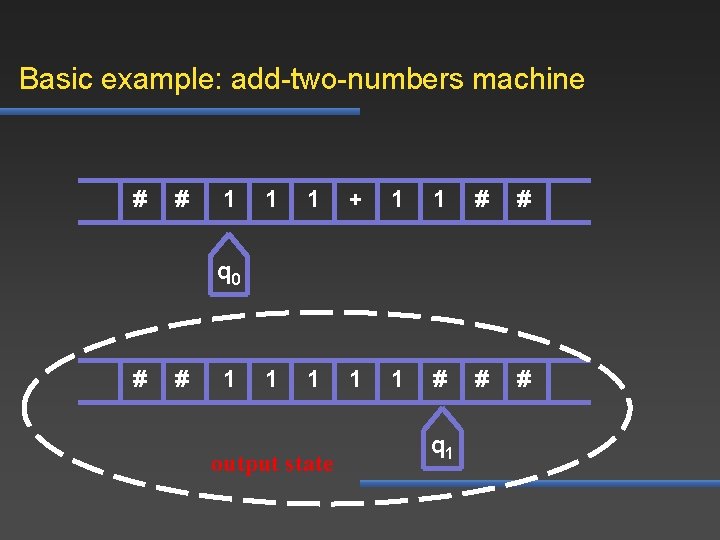
Basic example: add-two-numbers machine # # 1 1 1 + 1 1 # # # q 0 # # 1 output state q 1
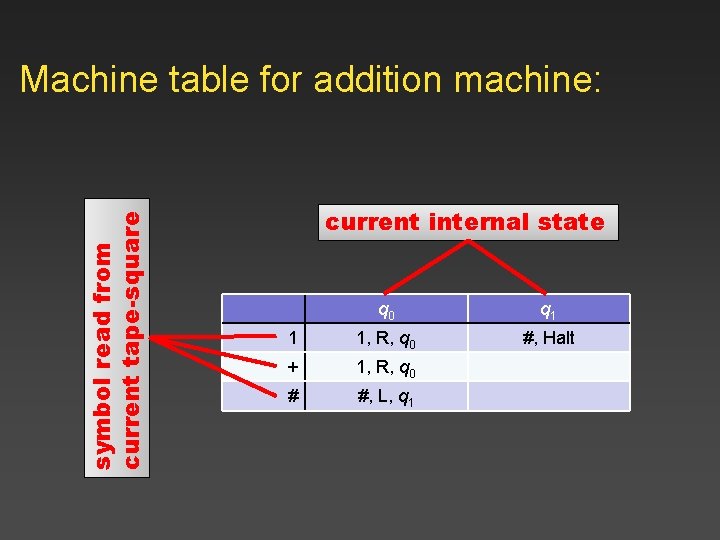
symbol read from current tape-square Machine table for addition machine: current internal state q 0 q 1 1 1, R, q 0 #, Halt + 1, R, q 0 # #, L, q 1

Basic example: add-two-numbers machine # # 1 q 0 1 1 + 1 1 # #

Basic example: add-two-numbers machine # # 1 1 q 0 1 + 1 1 # #

Basic example: add-two-numbers machine # # 1 1 1 q 0 + 1 1 # #

Basic example: add-two-numbers machine # # 1 1 1 + q 0 1 1 # #

Basic example: add-two-numbers machine # # 1 1 q 0 1 1 # #

Basic example: add-two-numbers machine # # 1 1 1 q 0 1 # #

Basic example: add-two-numbers machine # # 1 1 1 q 0 # #

Basic example: add-two-numbers machine # # 1 1 1 # q 0 #

Basic example: add-two-numbers machine # # 1 1 1 # q 1 # #

Physical realizations of Turing machines § we just described ‘parts’ of Turing machines. • but these ‘parts’ were abstract specifications. • not physical, nuts-and-bolts machines § To realize (or implement) a Turing machine, we need to build a physical system that satisfies the formal description of the machine. • • 1. symbols given concrete embodiments 2. transitions of physical device from state to state must ‘mirror’ structure of abstract Turing machine states
- Slides: 17