8 Wave Guides and Cavities 8 A Wave



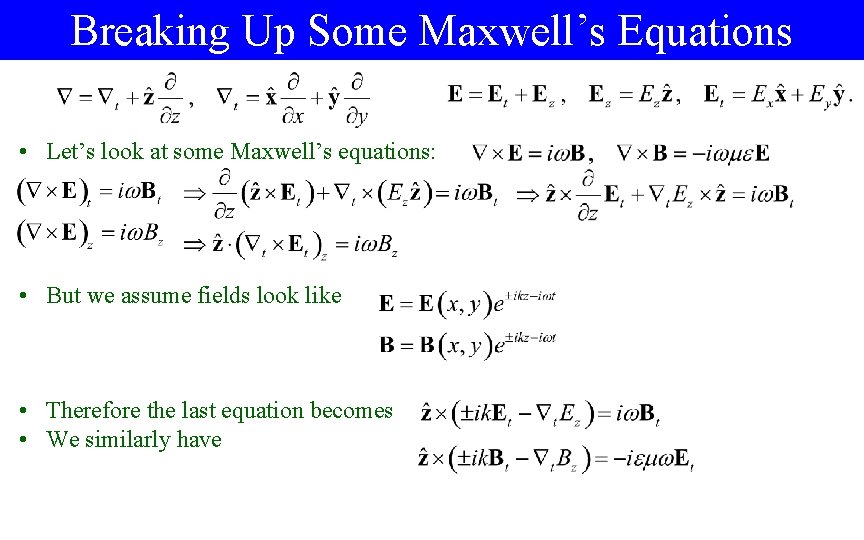























- Slides: 27

8. Wave Guides and Cavities 8 A. Wave Guides Boundary Conditions at Perfect Conductors • • Suppose we have a region bounded by a conductor We want to consider oscillating fields in the non-conducting region For oscillating fields, changing B would imply non-zero E But E must vanish in the conductor • • • On the surface of the conductors, and J are present Which appear in two of Maxwell’s equations Therefore, D and H|| need not be continuous But E|| and B must be continuous So the correct boundary conditions must be

Cylindrical Wave Guides • Consider now a hollow infinite cylinder of arbitrary cross-section – We’ll make it along the z-direction • We want to find solutions moving along the cylinder • Assume it is filled with a linear material: • We will use complex notation – Time-dependence will look like e-i t • Maxwell’s equations with no sources • Use linearity plus time dependence • Take curl of either of the last two equations: • Use the double cross-product rule • And therefore

Transverse and Longitudinal Dependence • Since we have translation dependence along z, it makes sense to look for solutions that go like e ikz – Moving in the z direction • Divide any derivative into transverse and longitudinal parts • Then we have, for example • Also break up fields into longitudinal and transverse parts: • We now want to write our Maxwell’s equations broken up this way
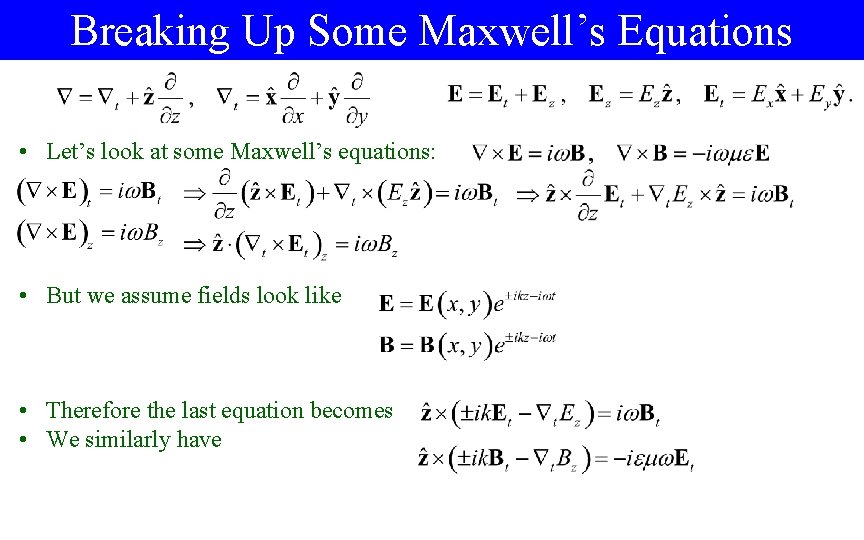
Breaking Up Some Maxwell’s Equations • Let’s look at some Maxwell’s equations: • But we assume fields look like • Therefore the last equation becomes • We similarly have

TEM Modes • Can we find solutions with Ez = Bz = 0? • Such modes are called TEM modes – Because both E and B are transverse • Then we would have • Multiplying the first by • But the left side is • We would therefore have – Implies phase velocity equal to free waves • Recall also • • And also This tells us finding Et is a 2 D electrostatic problem Recall also that potential is constant on surfaces Only get non-trivial solutions if there at least two conducting surfaces

Sample Problem 8. 1 A coaxial cable has inner radius a and outer radius b, and is filled with a material with electric permittivity and magnetic susceptibility . Find exact electric and magnetic field solutions for TEM modes. • We will start by finding the electric field, which is transverse and satisfies • Since it has no curl, it is derivable from a potential • Potential must be constant on the inner and outer surfaces • Symmetry implies that Et must be radial: • No divergence tells us: • Put back in the z- and t-dependence • Where: • The magnetic field is then • Take real part to get actual fields

All We Need is the Z-Direction of the Fields • Now consider non-TEM modes – Ez or Bz are non-zero • Multiply second equation by i and substitute the first one • For a transverse vector, • We therefore have • Solve for Et: • Also recall • Normally you have just Bz or Ez – Modes with Ez= 0 are called TE modes (transverse electric) – Modes with Bz = 0 are called TM modes (transverse magnetic)

Finding Non-TEM modes • All modes of E and B satisfy • Let us define • Then our equations become • We must also satisfy our boundary conditions

TE Modes Case 1: TE modes (transverse electric) • Search for solutions with Ez = 0, so everything comes from Bz • The transverse fields are then • We must also satisfy boundary conditions • These imply t. Bz must be parallel to the walls of the cylinder • Solve the eigenvalue equation subject to the boundary conditions

TM modes Case 2: TM modes (transverse magnetic) • Search for solutions with Bz = 0, so everything comes from Ez • The transverse fields are then • We must also satisfy the boundary conditions • These imply that Ez must vanish on the walls • Solve the eigenvalue equation subject to the boundary conditions

Sample Problem 8. 2 (1) A hollow cylindrical waveguide has circular cross-section of radius a. Find the relationship between the frequency and wave number for the lowest frequency modes for the TE and TM modes. • The frequencies are given by • The 2 values are eigenvalues of the equation – Where is Bz (TE) or Ez (TM) modes • Makes sense to work in cylindrical coordinates • Rotational symmetry implies solutions of the form • Substitute in: • Let • Then we have

Sample Problem 8. 2 (2) A hollow cylindrical waveguide has circular cross-section of radius a. Find the relationship between the frequency and wave number for the lowest frequency modes for the TE and TM modes. • • • This is Bessel’s Equation Solutions are Bessel functions Recall that represents Bz or Ez And we have boundary conditions We therefore must have • Let xmn be the roots of Jm and let ymn the roots of its derivative • Then the formula for the frequencies will be:

Sample Problem 8. 2 (3) A hollow cylindrical waveguide has circular cross-section of radius a. Find the relationship between the frequency and wave number for the lowest frequency modes for the TE and TM modes. • Maple is happy to find roots of Bessel’s equation > for m from 0 to 3 do evalf(Bessel. JZeros(m, 1. . 3)) end do; • With a little coaxing we can also get it to find the y’s > for m from 0 to 3 do seq(fsolve(diff(Bessel. J(m, x), x=(n+m/2 -3/4)*Pi), n=1. . 3) end do;

Comments on Modes • Note that for each mode, there is a minimum frequency • If you are at a limited , only a finite number of modes are possible – Usually a good thing – Ideally, want only one mode • The lowest mode is usually a TE mode • Note that the lowest modes often have m > 1 – Actually represent two modes because modes can be e im

8 B. Rectangular Wave Guides Working out the Modes • Let’s now consider a rectangular wave guide – Dimension a b with a b • We will work in Cartesian coordinates • Boundary conditions: • For TE modes, we want waves of the form • For TM modes, we want waves of the form • In each case, we have a b

Restrictions on Modes • For the TM modes (Ez), we must have m > 0 and n > 0 • For the TE modes (Bz), we can’t have m = 0 and n = 0 – Since then Bz has no transverse derivative • Hence TE modes have m > 0 OR n > 0 • Degeneracy between TE mode and TM mode if both positive • Lowest frequency mode: TE mode with (m, n) = (1, 0) • Second lowest modes: modes with b a (m, n) = (2, 0) or (0, 1) • If a 2 b, then factor of two difference between lowest and next lowest modes • Normally make a 2 b

The TE 10 mode • We can work out all the fields for the TE 10 mode – Put back in the z and t dependence • We then work out all the other pieces using • We therefore have • The factors of i represent a phase shift between the various modes a b

8 C. Cavities Cylindrical Cavities • Let’s now cap off the cylindrical cavity, make the ends conducting • Let it be along z with z from 0 to d • On the end, we must have • This means at z = 0 and z = d, we have • We have up until now used modes with • We no longer want e ikz, instead we want • We will have to take linear combinations of our previous solutions d

TE Modes in Cavities • For TE modes, we had • But we also need • We therefore must have Bz to be like • To get it to vanish at z = d, must have • So Bz is given by • To get the transverse components, take same linear combinations: d

TM Modes in Cavities • For TM modes, we had • • • But we also need We have to make the two contributions to Et cancel at z = 0, d This can be done if Ez is like To get it to work at z = d, must have So Ez is given by • To get the transverse components, take same linear combinations: d

Rules for Cavities Summarized • For both TE and TM modes, we have – k > 0 for TE, k 0 for TM • We have to solve the equation – represents Bz for TA and Ez for TM • Boundary conditions for TE: • Boundary conditions for TM: • For TM modes, we then have d

Box-Shaped Cavities • Consider a cavity of dimensions a b d • Frequency is given be • Where k is given by – p = 1, 2, 3, … for TE – p = 0, 1, 2, … for TM • In both cases, we had – m > 0 OR n > 0 for TE – m > 0 AND n > 0 for TM • Therefore, our frequencies are: • At least two of m, n, p must be non-zero – If m = 0 or n = 0, it is a TE mode – If p = 0, it is a TM modes – If all three are non-zero, it can be a TE or TM mode d a b

Sample Problem 8. 2 (1) A conducting box-shaped cavity has dimensions a b d. Write explicitly the form of all fields for the TE 1, 0, 1 mode, and find the energy in electric and magnetic fields as a function of time. • For TE modes, we first solve – Where is Bz • The 1, 0 solution is – I arbitrarily included 2/ 2 • is given by • Next find Bz: • Where k is given by • So we have d a b

Sample Problem 8. 2 (2). . . Write explicitly the form of all fields for the TE modes, and find the energy in electric and magnetic fields as a function of time. • Now let’s get Bt: • And finally, let’s go for Et: • We will also need the frequencies, which are given by

Sample Problem 8. 2 (3). . . find the energy in electric and magnetic fields as a function of time. • Keep in mind that we need to take the real part of these expressions • The electric energy density is: • Total electric energy is

Sample Problem 8. 2 (4). . . find the energy in electric and magnetic fields as a function of time. • Again, take the real part • Now let’s go for the magnetic energy density:

Sample Problem 8. 2 (5) A conducting box-shaped cavity has dimensions a b d. Write explicitly the form of all fields for the TE 1, 0, 1 mode, and find the energy in electric and magnetic fields as a function of time. d • It is pretty easy to see that • Of course, this is just conservation of energy a b
 Scout and guide law
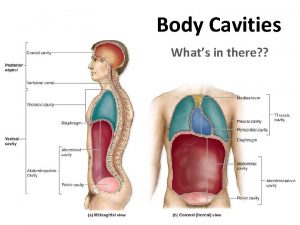
Scout and guide law The anterior and posterior body cavities
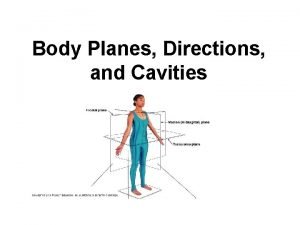
The anterior and posterior body cavities Chapter 7 2 body planes directions and cavities
Chapter 7 2 body planes directions and cavities Chapter 7.2 body planes, directions, and cavities
Chapter 7.2 body planes, directions, and cavities Classification of body membranes
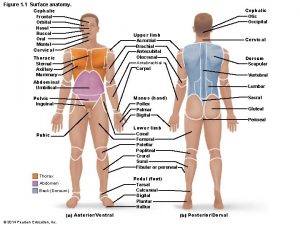
Classification of body membranes Labeling body planes directions and cavities
Labeling body planes directions and cavities Left lower quadrant organs
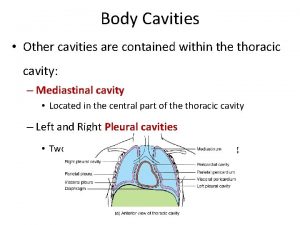
Left lower quadrant organs Vertebral cavity
Vertebral cavity Body directions and planes
Body directions and planes Body cavity
Body cavity Anticipation guide examples
Anticipation guide examples Othello act 2
Othello act 2 Unisa library guide
Unisa library guide Iuss standards
Iuss standards Objectives of strategic planning in retailing
Objectives of strategic planning in retailing Smart guides adobe illustrator
Smart guides adobe illustrator Cylinder head guides
Cylinder head guides Association of ukrainian guides
Association of ukrainian guides Unit meeting activities guides
Unit meeting activities guides Erg yellow section
Erg yellow section Munis training manual
Munis training manual Whose voice guides your choice
Whose voice guides your choice Wwc practice guides
Wwc practice guides God guides me
God guides me The person who guides
The person who guides Jhuma biswas
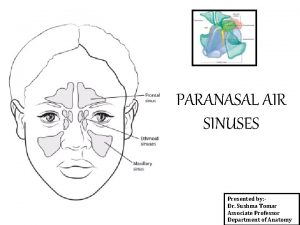
Jhuma biswas Air containing cavities in the bones around the nose
Air containing cavities in the bones around the nose Five body cavities
Five body cavities