421 420 410 4 2 411 401 320

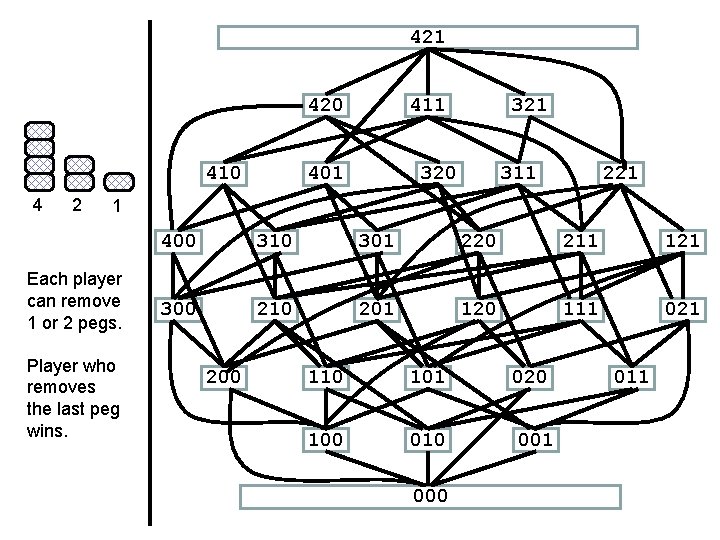
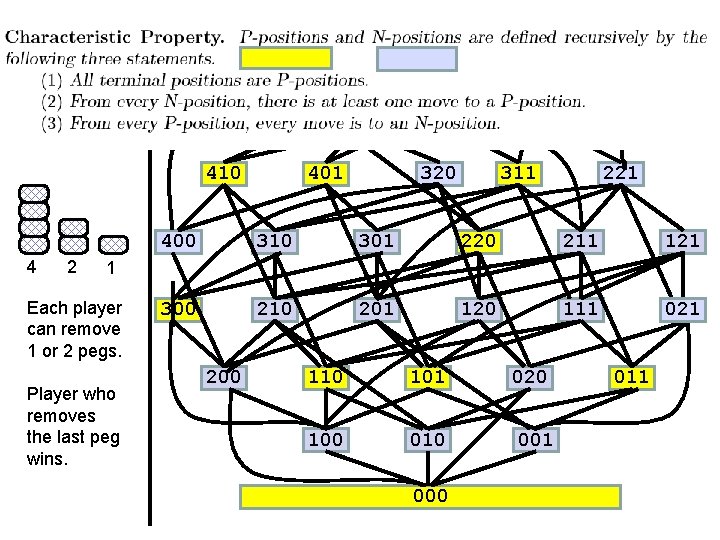
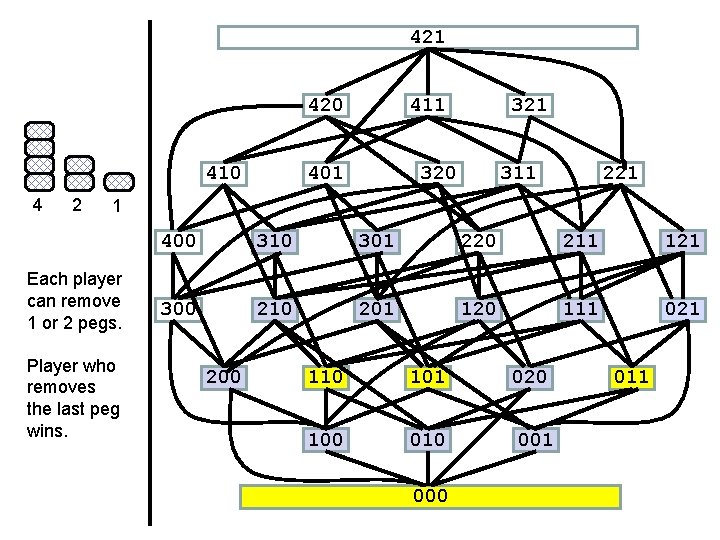
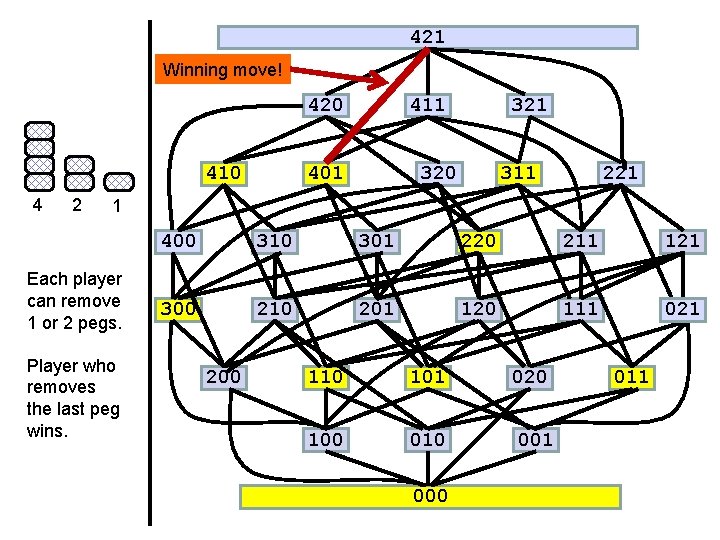
421 420 410 4 2 411 401 320 311 221 1 Each player can remove 1 or 2 pegs. Player who removes the last peg wins. 400 310 301 220 211 121 300 210 201 120 111 021 200 110 101 020 100 010 001 000 011

420 410 4 2 411 401 320 311 221 400 310 301 220 211 121 300 210 201 120 111 021 1 Each player can remove 1 or 2 pegs. Player who removes the last peg wins. 200 110 101 020 100 010 001 000 011

Determining P and N positions

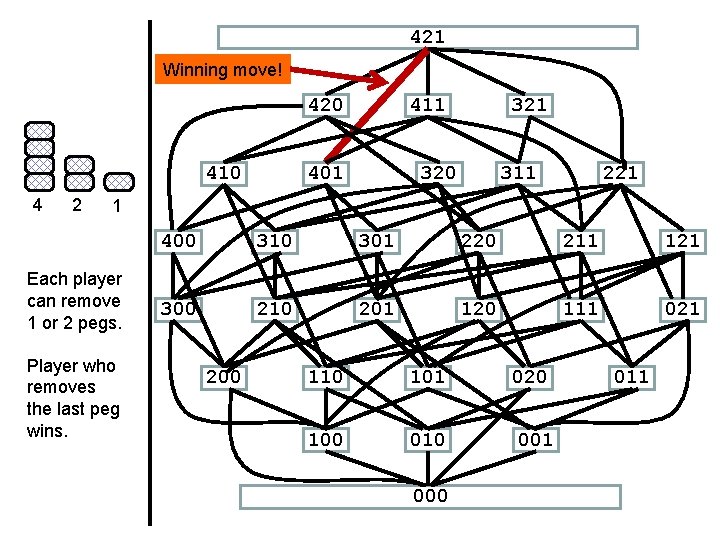
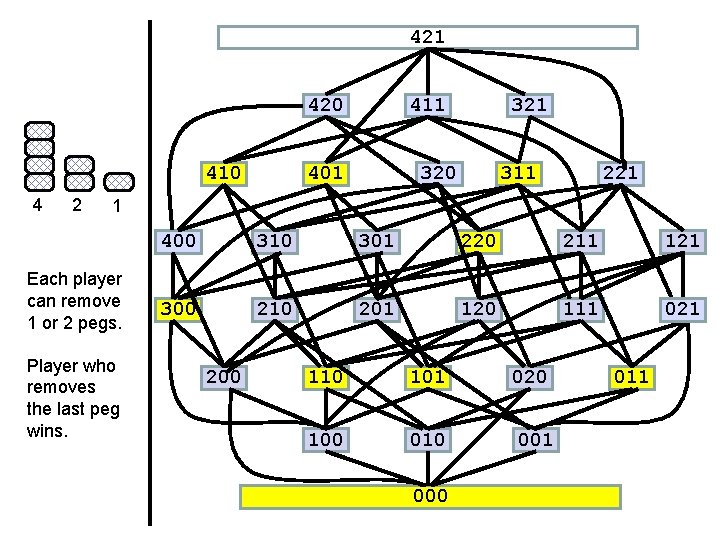
421 Winning move! 420 410 4 2 411 401 320 311 221 1 Each player can remove 1 or 2 pegs. Player who removes the last peg wins. 400 310 301 220 211 121 300 210 201 120 111 021 200 110 101 020 100 010 001 000 011

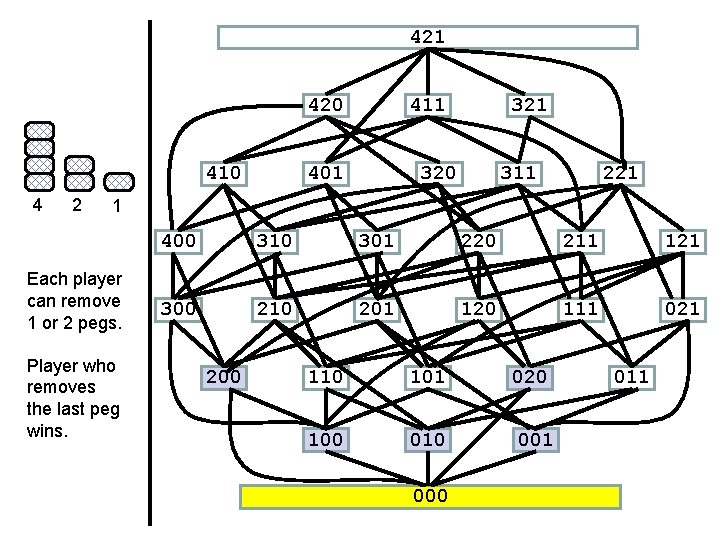
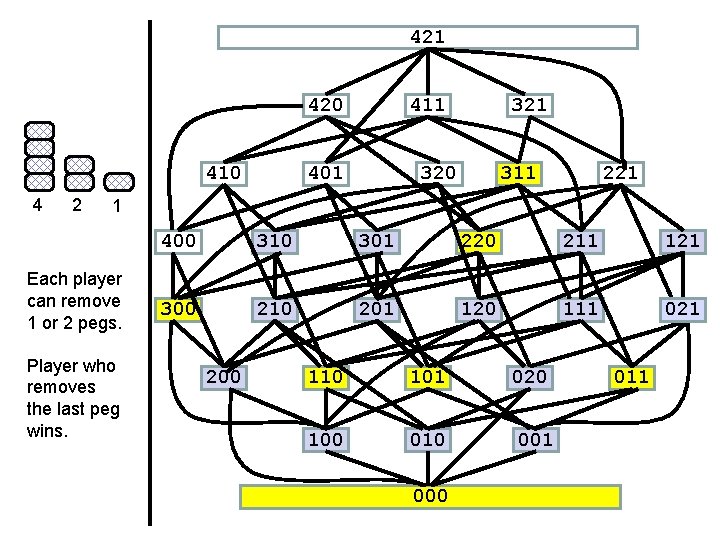
421 420 410 4 2 411 401 320 311 221 1 Each player can remove 1 or 2 pegs. Player who removes the last peg wins. 400 310 301 220 211 121 300 210 201 120 111 021 200 110 101 020 100 010 001 000 011

421 420 410 4 2 411 401 320 311 221 1 Each player can remove 1 or 2 pegs. Player who removes the last peg wins. 400 310 301 220 211 121 300 210 201 120 111 021 200 110 101 020 100 010 001 000 011

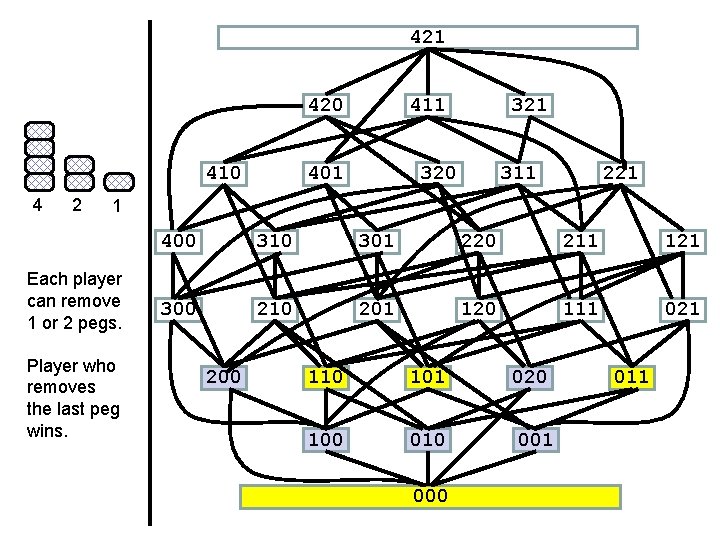
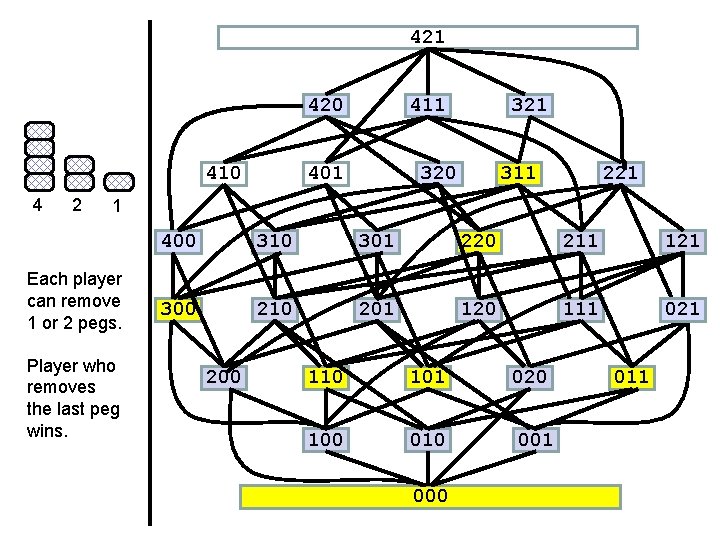
421 420 410 4 2 411 401 320 311 221 1 Each player can remove 1 or 2 pegs. Player who removes the last peg wins. 400 310 301 220 211 121 300 210 201 120 111 021 200 110 101 020 100 010 001 000 011

421 420 410 4 2 411 401 320 311 221 1 Each player can remove 1 or 2 pegs. Player who removes the last peg wins. 400 310 301 220 211 121 300 210 201 120 111 021 200 110 101 020 100 010 001 000 011

421 420 410 4 2 411 401 320 311 221 1 Each player can remove 1 or 2 pegs. Player who removes the last peg wins. 400 310 301 220 211 121 300 210 201 120 111 021 200 110 101 020 100 010 001 000 011

421 420 410 4 2 411 401 320 311 221 1 Each player can remove 1 or 2 pegs. Player who removes the last peg wins. 400 310 301 220 211 121 300 210 201 120 111 021 200 110 101 020 100 010 001 000 011

421 Winning move! 420 410 4 2 411 401 320 311 221 1 Each player can remove 1 or 2 pegs. Player who removes the last peg wins. 400 310 301 220 211 121 300 210 201 120 111 021 200 110 101 020 100 010 001 000 011

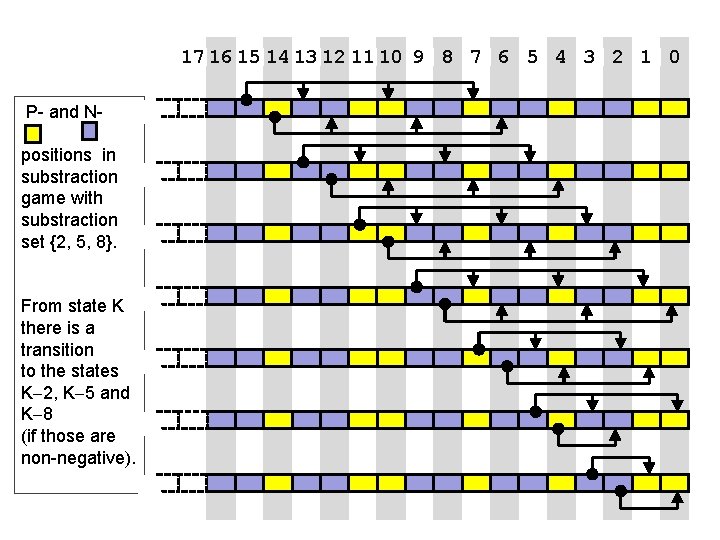
17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 P- and Npositions in substraction game with substraction set {2, 5, 8}. From state K there is a transition to the states K 2, K 5 and K 8 (if those are non-negative).

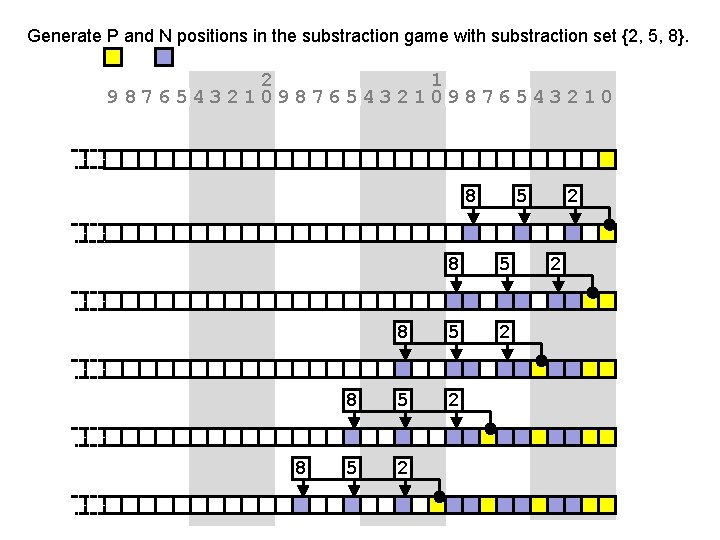
Generate P and N positions in the substraction game with substraction set {2, 5, 8}. 2 1 98765432109876543210 8 8 5 8 5 2 5 2 2 2

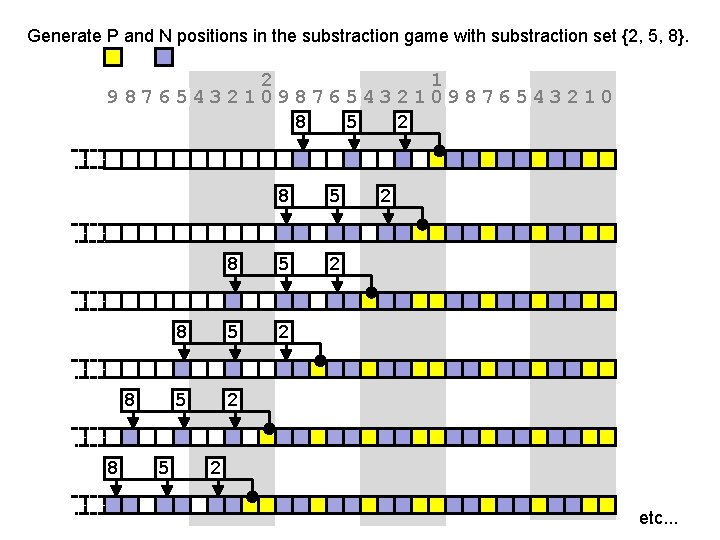
Generate P and N positions in the substraction game with substraction set {2, 5, 8}. 2 1 98765432109876543210 8 5 2 8 8 5 8 5 2 5 2 2 2 etc. . .

Binary representation of positive integers in Fibonacci base: . . . 34 21 13 N= 1 0 0 0 2 0 0 0 3 0 0 0 4 0 0 0 5 0 0 0 6 0 0 0 7 0 0 0 8 0 0 0 9 0 0 0 10 0 11 0 0 0 12 0 0 0 13 0 0 14 0 0 15 0 0 16 0 0 17 0 0 18 0 0 19 0 0 1 0 20 0 0 1 0 21 0 0 22 0 1 0 0 23 0 1 0 0 24 0 1 0 0 base: 8 0 0 0 0 1 0 1 0 1 0 0 0 5 0 0 0 1 0 1 0 0 0 1 0 1 0 0 3 0 0 1 0 0 0 0 1 0 1 0 0 0 0 0 1 2 0 1 0 0 0 0 0 1 0 1 1 0 0 0 1 0 0 0 1 0 0 . . . 55 34 21 13 0 0 N = 25 0 0 1 26 0 0 1 0 0 27 0 0 1 0 0 28 0 0 1 0 0 29 0 0 1 0 0 30 0 0 1 0 0 31 0 0 32 0 0 1 0 0 33 0 0 1 0 0 34 0 1 0 0 0 35 0 1 0 0 0 36 0 1 0 0 0 37 0 1 0 0 0 38 0 1 0 0 0 39 0 1 0 0 0 40 0 1 0 0 0 41 0 0 0 42 0 1 0 0 0 43 0 1 0 0 0 44 0 1 0 0 0 45 0 1 0 0 0 46 0 1 0 0 0 47 0 1 0 48 0 1 0 8 0 0 0 1 0 1 0 1 0 0 5 0 0 1 0 1 0 0 0 1 0 0 0 0 3 0 1 0 1 0 0 0 0 1 0 0 2 0 1 0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 1 0 0 0 1 0 0 1

Fibonacci Nim: base: One pile of tokens. First player can remove 1 or more tokens but not all of them. Next, each player than can remove at most twice the number of tokens removed in his oponent's last move. Player who removes last token wins. Let: N be the current number of tokens. Rem. Lim be maximum tokens which can be currently removed. Fmin be the rightmost base element present in N (rightmost 1). Then: Rem. Lim < Fmin. . . . P-position Rem. Lim >= Fmin. . . . N-position Rule: In N-position remove Fmin tokens. . 55 34 21 13 0 0 N = 25 0 0 1 26 0 0 1 0 0 27 0 0 1 0 0 28 0 0 1 0 0 29 0 0 1 0 0 30 0 0 1 0 0 31 0 0 32 0 0 1 0 0 33 0 0 1 0 0 34 0 1 0 0 0 35 0 1 0 0 0 36 0 1 0 0 0 37 0 1 0 0 0 38 0 1 0 0 0 39 0 1 0 0 0 40 0 1 0 0 0 41 0 0 0 42 0 1 0 0 0 43 0 1 0 0 0 44 0 1 0 0 0 45 0 1 0 0 0 46 0 1 0 0 0 47 0 1 0 48 0 1 0 8 0 0 0 1 0 1 0 1 0 0 5 0 0 1 0 1 0 0 0 1 0 0 0 0 3 0 1 0 1 0 0 0 0 1 0 0 2 0 1 0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 1 0 0 0 1 0 0 1

Rem. Lim < Fmin. . . . P-position Rem. Lim >= Fmin. . . . N-position base: . . . 55 34 21 13 0 0 N = 25 0 0 1 Example: 26 0 0 1 0 0 Pile with 45 tokens. 27 0 0 1 0 0 28 0 0 1 0 0 29 0 0 1 0 0 First move: 30 0 0 1 0 0 N = 45, Rem. Lim = 44, Fmin = 3. 31 0 0 Rem. Lim >= Fmin. . N-position 32 0 0 1 0 0 33 0 0 1 0 0 Remove Fmin: N = 45 3 = 42 34 0 1 0 0 0 35 0 1 0 0 0 36 0 1 0 0 0 Next move: 37 0 1 0 0 0 The opponent can remove 1 to 6 38 0 1 0 0 0 tokens, that is, he can set the pile 39 0 1 0 0 0 40 0 1 0 0 0 to 41, 40, 39, 38, 35 tokens. 41 0 0 0 42 0 1 0 0 0 All these are N-positions, because 43 0 1 0 0 0 44 0 1 0 0 0 Rem. Lim = 6, Fmin <= 5. 45 0 1 0 0 0 46 0 1 0 0 0 47 0 1 0 48 0 1 0 8 0 0 0 1 0 1 0 1 0 0 5 0 0 1 0 1 0 0 0 1 0 0 0 0 3 0 1 0 1 0 0 0 0 1 0 0 2 0 1 0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 1 0 0 0 1 0 0 1

Rem. Lim < Fmin. . . . P-position Rem. Lim >= Fmin. . . . N-position base: . . . 55 34 21 13 0 0 N = 25 0 0 1 Example continues: 26 0 0 1 0 0 27 0 0 1 0 0 Opponent took 4. 28 0 0 1 0 0 Pile with 38 tokens. 29 0 0 1 0 0 30 0 0 1 0 0 Next move: 31 0 0 32 0 0 1 0 0 N = 38, Rem. Lim = 8, Fmin = 1. 33 0 0 1 0 0 Rem. Lim >= Fmin. . N-position 34 0 1 0 0 0 Remove Fmin: N = 38 1 = 37 35 0 1 0 0 0 36 0 1 0 0 0 37 0 1 0 0 0 Next move: 38 0 1 0 0 0 The opponent can remove 1 or 2 39 0 1 0 0 0 tokens, that is, he can set the pile 40 0 1 0 0 0 41 0 0 0 to 36 or 35 tokens. 42 0 1 0 0 0 43 0 1 0 0 0 All these are N-positions, because 44 0 1 0 0 0 45 0 1 0 0 0 Rem. Lim = 2, Fmin <= 3. 46 0 1 0 0 0 47 0 1 0 48 0 1 0 8 0 0 0 1 0 1 0 1 0 0 5 0 0 1 0 1 0 0 0 1 0 0 0 0 3 0 1 0 1 0 0 0 0 1 0 0 2 0 1 0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 1 0 0 0 1 0 0 1