1 2 Cenni di relativit ristretta 1 2

1. 2 Cenni di relatività ristretta • • • 1. 2. 1 Gli albori 1. 2. 2 L'esperimento di Michelson-Morley 1. 2. 3 Trasformazioni di Lorentz 1. 2. 4 Cinematica relativistica 1. 2. 5 Lo scattering Compton 1. 2. 6 Unità di misura

1. 2. 1 Gli albori Le leggi del moto enunciate da Newton furono espresse per moto in un sistema di riferimento assoluto. Tuttavia esse funzionano anche per "sistemi inerziali" – in moto relativo costante rispetto a questo. Il principio di relatività Galileiano stabilisce che le leggi della meccanica che governano sistemi in moto relativo rettilineo uniforme gli uni rispetto agli altri (sistemi inerziali) hanno identica forma non c'è modo di distinguerli con esperimenti fisici Galileo espresse questo principio nel 1632 considerando una nave in moto in un mare piatto: esperimenti sotto coperta non permettono allora di decidere se la nave è in moto o ferma Il principio permette di enunciare leggi di trasformazione delle velocità, esprimibili in un sistema di riferimento in moto rispetto a un altro. Ad esempio una barca in un fiume, che si muove rispetto alla corrente (in moto rispetto a terra con velocità vcorrente) con velocità vbarca, sarà visibile da terra in moto con velocità vterra = vbarca + vcorrente Verso la fine dell'Ottocento si riconobbe (Mach, Lorentz) che la legge della trasformazione delle velocità non si può applicare alle onde elettromagnetiche. A questo enigma diede soluzione Einstein nel 1905.

Formule di trasformazione Galileiana Se ho un sistema S' in moto rispetto a S con velocità v costante lungo l'asse x, in S' valgono le stesse leggi fisiche, nelle coordinate: – – t' = t x' = x – vt y' = y z' = z L'invarianza del tempo permette di verificare la legge di trasformazione delle velocità: dx'/dt' = dx'/dt = dx/dt – v Questa formula non funziona più se le velocità in gioco sono non trascurabili rispetto alla velocità della luce. Per descrivere il moto delle particelle elementari, ad esempio, ci servono regole diverse. La meccanica Newtoniana e le leggi di Galileo devono allora essere sostituite con quelle della Meccanica relativistica e della relatività ristretta.

1. 2. 2 L'esperimento di Michelson-Morley Tutti i moti ondulatori conosciuti nell'Ottocento erano perturbazioni di un mezzo materiale per le onde EM si immagina un "etere" – senza massa, non offre resistenza al moto dei corpi. E' un sistema di riferimento con tutte le proprietà del sistema assoluto di Newton. In generale la velocità di un'onda rispetto al mezzo dipende solo dalle proprietà del mezzo, e non dal moto della sorgente. Questo fu assunto valere anche per la luce. Se la luce si muove con velocità c rispetto all'etere, la sua velocità rispetto a un corpo in moto nell'etere (e. g. la terra) dovrebbe cambiare secondo le leggi di trasformazione delle velocità misurando la velocità della luce in diverse direzioni sulla terra si potrebbe determinare la velocità della terra rispetto all'etere Lo stesso vale per le forze EM, governate dalle equazioni di Maxwell che descrivono anche il moto delle onde EM (e la loro velocità) A fine Ottocento si fecero molti esperimenti per determinare variazioni nella velocità della luce o nella forza fra cariche elettriche. L'esperimento che diede la risposta definitiva sull'assenza dell'etere fu ideato da Michelson e Morley.

Setup dell'esperimento Nel 1887 Michelson e Morley costruirono un interferometro per rivelare variazioni nel tempo di percorrenza di raggi di luce perpendicolari fra loro La differenza di tempo di percorrenza dei due cammini luminosi è δt = L/(c-v) + L/(c+v) – 2 L/(c 2 -v 2)0. 5 = = 2 Lc/(c 2 -v 2)[1 -(1 -v 2/c 2)0. 5] = 2 L/(c 2 -v 2)[v 2/2 c] che è approssimativamente eguale a δt = Lv 2/c 3 Quindi per luce di lunghezza d'onda λ la differenza di fase fra i due raggi sarà cδt/λ = (v/c)2 L/λ.

Risultati La rotazione di 90° dell'apparato (possibile grazie al floating su mercurio dell'interferometro) dovrebbe permettere di estrarre una differenza di fase pari al doppio di quanto calcolato sopra. Usando riflessione multipla con diversi specchi M&M ottennero una lunghezza effettiva L=11 m, che con vterra=3*104 m/s dovrebbe dare uno spostamento di 0. 4 frange di interferenza per luce visibile (λ=0. 5μm), facilmente rivelabile giacché lo strumento era sensibile a spostamenti di 0. 01 frange. Ma. . . Non si osservò alcuno shift, nemmeno in diverse stagioni (per verificare che non vi fossero effetti di stazionarietà della terra rispetto all'etere in determinati punti dell'orbita) o luoghi della superficie terrestre (in montagna, per verificare l'ipotesi di Stokes secondo cui la superficie terrestre esercita un "drag" sull'etere)

Interpretazione dei risultati Michelson provò a ripetere l'esperimento su una montagna, per rispondere a un'obiezione di Stokes (l'etere viene "trascinato" dalla superficie terrestre), ma trovò gli stessi risultati. Una possibile spiegazione della non rivelazione di phase shift è che la luce si muova a velocità c rispetto alla sorgente (Ritz). Ma questo si può confutare osservando sistemi stellari binari. La stella in moto intorno al centro di massa emetterà luce con velocità variabile fra c-v e c+v rispetto a un osservatore solidale con il CM; anche se v è piccolo rispetto a c, le quantità in gioco fanno sì che si dovrebbe osservare una violazione della legge di Keplero (vedi articolo di Sotina). Furono Fitzgerald e Lorentz a dare la spiegazione corretta: il braccio dell'interferometro parallelo al moto della terra si accorcia del fattore (1 -v 2/c 2)0. 5 cosicché non si osserva interferenza. L'effetto non è osservabile perché qualunque strumento di misura si accorcia dello stesso fattore! Nel 1904 Lorentz descrisse una teoria elettronica della materia in cui spiegò il fenomeno con modifiche alle forze EM che tengono insieme i corpi quando questi si muovono rispetto all'etere. Egli basò le sue conclusioni su un nuovo set di leggi di trasformazione delle coordinate. Nel 1905 Einstein pubblicò l'articolo "On the Electrodynamics of Moving Bodies" in cui enunciò la sua teoria della relatività speciale. I suoi risultati sono gli stessi di quelli di Lorentz, ma la sua filosofia è fondamentalmente diversa. Se non si può rivelare l'etere, non ha senso parlare di moto rispetto ad esso. . .

1. 2. 3 Trasformazioni di Lorentz Se la velocità di un sistema di riferimento modifica la dimensione spaziale nella direzione del moto, anche il tempo ne risente. La nostra nozione di tempo è legata a come lo misuriamo. La nozione di simultaneità viene scardinata dalle trasformazioni di Lorentz. Scopriremo che un orologio in moto misura il tempo più lentamente di uno stazionario. Se A e B sono in moto relativo, ciascun osservatore vede l'orologio dell'altro in ritardo rispetto al suo! Il paradosso si supera chiedendosi cos'è la simultaneità. Se non esiste un tempo assoluto, possiamo comunque definire intervalli di tempo in un punto dello spazio, e tutti gli osservatori concorderanno su essi; ma per confrontare il timing di eventi che avvengono in punti diversi dello spazio, è necessario mandare un segnale da uno all'altro punto. A causa di ciò, osservatori in moto relativo si troveranno in disaccordo sulla simultaneità degli eventi osservati. Vediamo un esempio. Un osservatore A manda due segnali luminosi in direzioni opposte verso rivelatori R 1 e R 2 a distanza L. Per lui, R 1 e R 2 rivelano la luce in simultaneità. Per un osservatore B che si muove con velocità v da R 1 a R 2, i segnali di luce si muovono con velocità c rispetto a se stesso; ma siccome rispetto a B R 1 e R 2 si muovono con velocità v, uno verso la sorgente e uno in direzione opposta, per lui R 1 e R 2 non rivelano la luce simultaneamente. La simultaneità è quindi un concetto relativo all'osservatore. A e B devono usare misure remote per decidere sulla simultaneità di conteggi di R 1 e R 2. Si basano entrambi sulla loro misura delle distanze A-R 1, A-R 2, B-R 1, B-R 2, ma a causa della contrazione delle lunghezze, non concordano sul loro valore, per cui devono anche essere discordi nel timing dei conteggi. B R 1 A R 2

Postulati di Einstein Nell'articolo del 1905, Einstein formula due postulati per la sua teoria della relatività speciale: - le leggi della fisica sono identiche in tutti i sistemi di riferimento inerziali la velocità della radiazione elettromagnetica nel vuoto è costante, e indipendente dal moto della sorgente - controintuitivo? Nega che le velocità si sommino linearmente (trasformazioni Galileiane della velocità) Oggi la definizione del metro nel SI è legata alla velocità della luce nel vuoto: c = 299792458 m/s Il secondo postulato di Einstein ci obbliga a legare spazio e tempo con nuove equazioni che governano le trasformazioni fra sistemi di riferimento, a causa della modifica delle leggi di trasformazione della velocità

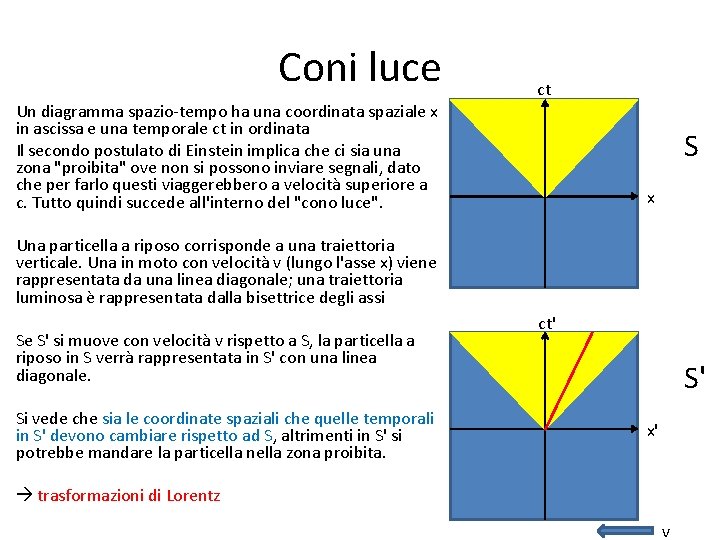
Coni luce ct Un diagramma spazio-tempo ha una coordinata spaziale x in ascissa e una temporale ct in ordinata Il secondo postulato di Einstein implica che ci sia una zona "proibita" ove non si possono inviare segnali, dato che per farlo questi viaggerebbero a velocità superiore a c. Tutto quindi succede all'interno del "cono luce". S x Una particella a riposo corrisponde a una traiettoria verticale. Una in moto con velocità v (lungo l'asse x) viene rappresentata da una linea diagonale; una traiettoria luminosa è rappresentata dalla bisettrice degli assi Se S' si muove con velocità v rispetto a S, la particella a riposo in S verrà rappresentata in S' con una linea diagonale. Si vede che sia le coordinate spaziali che quelle temporali in S' devono cambiare rispetto ad S, altrimenti in S' si potrebbe mandare la particella nella zona proibita. ct' S' x' trasformazioni di Lorentz v

Trasformazioni di Lorentz •

Trasformazione delle velocità •

Dilatazione dei tempi Consideriamo un intervallo di tempo misurato in una posizione fissa x ( non dobbiamo preoccuparci del concetto di simultaneità e della trasmissione di segnali, nel descrivere l'intervallo) da un sistema stazionario S Δt = t 2 – t 1 Possiamo chiederci come un osservatore in un sistema S' misurerà questo intervallo. Dobbiamo usare le leggi di trasformazione di Lorentz: Δt' = t 2'-t 1' = γ(t 2 -xv/c 2) – γ(t 1 -xv/c 2) = γ(t 2 -t 1) = γΔt Vediamo che il tempo, osservato da S', appare scorrere più lentamente. Questo risultato è una conseguenza diretta del secondo postulato della relatività speciale

Un esempio Supponiamo che un impulso luminoso sia emesso da A e rivelato in B, nel sistema S S' sia in moto rispetto a S con velocità v ortogonale a AB (cosicché quella coordinata non viene influenzata dal moto) In S, il tempo necessario alla propagazione del segnale è Δt = L/c In S', il percorso del fotone è più lungo, perché da quando parte da A, il fotone viene visto viaggiare in diagonale per raggiungere B, che nel frattempo si è spostato dalla verticale per via del moto relativo di S'. Si trova Δt' = L / (c 2 -v 2)0. 5 = γL/c Il tempo, misurato nel sistema S', è dunque dilatato di un fattore gamma. L'orologio di S' va "più lento"! Per qualunque misura di intervalli di tempo, c'è un sistema di riferimento in cui l'orologio è a riposo; rispetto a quello, sistemi in moto subiscono una dilatazione dei tempi. B S' A v (c 2 -v 2)0. 5 A c v

Contrazione delle lunghezze Consideriamo un righello che si muove rispetto a un orologio fermo, in S. Ne misuriamo la lunghezza verificando quanto tempo ci mettono gli estremi a passare davanti all'orologio: L = v Δt Nel sistema in cui il righello è fermo, è l'orologio a muoversi con velocità v. Qui il passaggio per i due estremi del righello permette di nuovo di determinare la lunghezza del righello come L' = v Δt' Poiché le misure di tempo in S' e S sono legate dalla trasformazione di Lorentz, sappiamo che Δt' = γΔt Ne risulta che L = L'/γ cioè la lunghezza del righello, misurata nel sistema in cui esso è a riposo, è maggiore (L'>L).

1. 2. 4 Cinematica relativistica Le formule classiche per energia cinetica e momento (quantità conservata in meccanica Newtoniana), sono Ek = 1/2 mv 2 p = mv Ovviamente queste formule non valgono per velocità non piccole rispetto a c: ad esempio, un protone di Ek=300 Ge. V avrebbe velocità v = (2 Ek/m)0. 5 = c(2 Ek/mc 2)0. 5 = 25 c ! Per accordarsi con le formule di trasformazione di Lorentz, il momento relativistico si scrive p = γmv e l'energia totale di una particella libera è E = γmc 2. Le due quantità sono legate dalla formula E = [(pc)2+(mc 2)2]0. 5 Per tutte le particelle vale v/c = pc/E, e per il fotone e qualunque altra particella di massa nulla vale quindi E=pc, o anche p=E/c.

Trasformazione di E e p Energia e momento di un corpo dipendono dal sistema di riferimento in cui sono misurate. Dalle trasformazioni delle velocità ottenute dalle leggi di Lorentz si trova l'espressione di E e p in diversi sistemi inerziali (β=v/c, γ=(1 -β 2)-0. 5): E' = γE – βγpxc p'xc = – βγE + γpxc p'yc = pyc p'zc = pzc Quindi se una particella è a riposo in S (E=p=0), in S', in moto rispetto a S con velocità v, ha E' = γmc 2, p' = γβmc: queste sono infatti E e P di una particella in moto con velocità v.

Notazione quadrivettoriale •

Esempio: energia nel centro di massa •

Esempio Due elettroni viaggiano l'uno verso l'altro. Nel sistema del laboratorio il primo ha velocità v 1=β 1 c e il secondo velocità v 2 = -β 2 c. Qual è la velocità del primo elettrone nel sistema di riferimento in cui il secondo elettrone è fermo? S 1 2 S' 1 2 L'energia-momento del primo elettrone è data da (E 1, p 1 c) = (γ 1 mc 2, γ 1β 1 mc 2) Facciamo una trasformazione di Lorentz con velocità β 2 c lungo l'asse x, cosicché "fermiamo" l'elettrone 2: per il primo elettrone avremo E' = γ 2 E + γ 2β 2 pc = γ 2γ 1 mc 2 + γ 2β 2γ 1β 1 mc 2 p'c = γ 2β 2 E + γ 2 pc = γ 2β 2 γ 1 mc 2 + γ 2γ 1β 1 mc 2 La velocità dell'elettrone 1 nel sistema in cui il secondo è a riposo è allora v'/c = p'c/E' = (γ 2β 2 γ 1 mc 2 + γ 2γ 1β 1 mc 2) / (γ 2γ 1 mc 2 + γ 2β 2γ 1β 1 mc 2) = = (β 2 + β 1) / (1 + β 1β 2) Notate il denominatore: la correzione β 1β 2 è ininfluente per velocità piccole, ma se sono confrontabili con c le cose cambiano. E. g. β 1=β 2=0. 5 v'/c = 0. 8 β 1=β 2=0. 9 v'/c = 0. 9945

1. 2. 5 Lo scattering Compton, spiegato da Compton nel 1923 (Nobel 1927), è un fenomeno comprensibile solo con la cinematica relativistica. Si tratta dello scattering di luce di alta frequenza (raggi X) da particelle cariche (e. g. elettroni). Lo scattering inelastico risulta in una modifica della direzione e anche della lunghezza d'onda della luce incidente – quest'ultimo fatto non è comprensibile con la teoria classica. La formula estratta da Compton spiega la dipendenza osservata del cambiamento di lunghezza d'onda dall'angolo di scattering. L'effetto dimostra che la luce ad alta energia si deve descrivere in modo corpuscolare per comprenderne i fenomeni Nell'esperimento di Compton i raggi X avevano un'energia di 17 ke. V; per questa energia gli elettroni atomici si comportano come liberi (l'energia di legame è molto inferiore) L'interazione è uno dei tre modi (effetto fotoelettrico e pair production sono gli altri due) in cui la luce interagisce con la materia

Descrizione del processo Il processo di scattering inelastico γ+e γ'+e può studiarsi in un sistema di riferimento in cui l'elettrone è a riposo, "sistema del laboratorio" 5 quantità descrivono (in modo ridondante) la cinematica: p 1, p 2, pe, e gli angoli θ e φ di fotone ed elettrone nello stato finale, rispetto alla direzione incidente Scriviamo le equazioni di conservazione di energia e momento: E: p 1 c + mc 2 = p 2 c + (pe 2 c 2+m 2 c 4)0. 5 e p x: p 1 c = p 2 c cosθ + pec cosφ py: 0 = -p 2 c sinθ + pec sinφ

Calcolo dell'impulso finale del fotone p 2 Per l'elettrone nello stato finale energia e momento si scrivono Ee = (pe 2 c 2 + m 2 c 4)0. 5 = p 1 c + mc 2 - p 2 c θ p 1 pec cosφ = p 1 c – p 2 c cosθ φ pec sinφ = p 2 c sinθ Da queste si trova l'equazione seguente: pe m 2 c 4 = (p 1 c + mc 2 - p 2 c)2 – pe 2 c 2 = = (p 1 c + mc 2 - p 2 c)2 – (p 1 c – p 2 c cosθ)2 – p 22 c 2 sin 2θ che con pochi conti si riduce a mc 2(p 1 c – p 2 c) = p 1 p 2 c 2(1 – cosθ) Questa fornisce la formula di Compton, che esprime p 2 in funzione dell'angolo di scattering: p 2 c = (mc 2 p 1 c) / [mc 2+p 1 c (1 – cos θ)] Si vede che per p 1 c<<mc 2 lo scattering è elastico: si trasferisce momento ma quasi nessuna energia. Questo è anche il limite per forward scattering (θ=0). Invertendo la formula e usando p=h/λ si può anche esprimere la variazione di lunghezza d'onda della luce incidente come (λ 2 -λ 1) = h/mc (1 – cosθ) Questa esprime chiaramente come il cambiamento in lunghezza d'onda è dipendente solo dall'angolo di scattering della luce.

1. 2. 6 Unità di misura Il sistema di misura internazionale SI è basato sul metro come unità di lunghezza, il secondo come unità di tempo, e il kilogrammo come unità di massa. Alla faccia degli inglesi. Tuttavia in fisica fondamentale è più opportuno utilizzare un sistema di "unità naturali", in cui si fissa a 1 il valore della velocità della luce c, e si fissa pure a 1 il valore di h/2π. La terza unità fondamentale è l'unità di energia, per cui si può scegliere l'elettronvolt, e. V, o i suoi multipli. Il più comodo è il Ge. V = 109 e. V. La conversione alle unità SI è la seguente: 1 Ge. V = 1. 602 10 -10 J h/2π = 1. 055 10 -34 Js = 6. 592 10 -25 Ge. V s c = 2. 9979 108 m/s

Considerazioni dimensionali Il definire come unitari c e h/2π ha implicazioni nel calcolo dimensionale. La velocità della luce ha dimensioni [c] = [L][T]-1 quindi se c=1, ne deriva che [L] = [T]. La possibilità di esprimere l'energia di onde EM come prodotto hc/λ e il momento come h/λ implica poi che se poniamo h/2π=1, abbiamo [E] = [T]-1 = [p] = [L]-1 Si vede che le dimensioni naturali dell'impulso sono l'inverso della distanza. Poiché poi h=E/ν, [h] = [M][L]2[T]-1, quindi [M] = [L]-1 = [T]-1 Tutto ciò implica che la relazione fra energia e impulso di una particella diventa semplicemente E 2 = p 2 + m 2. Quindi si parla semplicemente di energia, impulso, e massa in Ge. V. La conversione in Ge. V di massa, lunghezza e tempo è data da 1 kg = 5. 607 1026 Ge. V 1 m = 5. 068 1015 Ge. V-1 1 s = 1. 519 1024 Ge. V-1

Esempi di domande possibili sul materiale visto nel cap. 1. 2 • Descrivi l'esperimento di Michelson e Morley e indicane i risultati principali • Quali sono i principi della relatività di Einstein e quali conseguenze fondamentali ne derivano? • Per un sistema di due elettroni che viaggiano uno verso l'altro nel laboratorio con velocità v 1 e v 2, calcola la velocità di un elettrone nel sistema in cui l'elettrone 2 è a riposo • Descrivi lo scattering Compton in termini qualitativi e fornisci la formula dello spostamento di lunghezza d'onda