09 Mathematik Lsungen ZAP 2007 a Mathematik KZO

09 Mathematik Lösungen ZAP 2007 a

Mathematik KZO 2007 a 1. Bestimme die Lösung. Alles in Meter! 680 m = 4. 52 km + m 680 m = 4520 m + m 24495 m 4520 m 19975 m = m

Mathematik KZO 2007 a 2. Gib die Lösung als Dezimalzahl an. Dezimalbruch: (1980 : 88) = : 7 27. 125 22. 5 = : 7 = = 4. 625 • 32. 375 7

Mathematik KZO 2007 a Wie viel Wasser bleibt in der Aprikose? = Restwasser: 85 g : 5 17 g Festanteil: 100 g 85 g = 15 g Restwasser: 17 g Von 100 g bleiben: 32 g Wie viel frische A. für 1. 6 kg dürre? : 2 • 100 : 5 32 g 1600 g 16 g Es braucht 5 kg frische für 1. 6 kg dürre Aprikosen. 100 g 50 g : 2 • 100

Mathematik KZO 2007 a 4. Eine fünfstellige Zahl mit der Quersumme 22 soll lauter verschiedene Ziffern haben. Dabei darf die Ziffer 0 wie üblich nicht an der vordersten Stelle stehen. a) Bestimme die grösste solche Zahl. Beginne mit der 9, dann die nächst kleinere usw. 98410 (98500 nicht erlaubt!) b) Bestimme die zweitgrösste solche Zahl. 98401 c) Bestimme die zweitkleinste solche Zahl. 10498 9 8 4 1 0 Quersumme: 9+8+4+1+0=22 (Quersumme 17) Bis zur Quersumme 22 fehlen noch 5 (Wert), dafür haben wir noch 3 Ziffern zur Verfügung. Das kann mit den Ziffern 4, 1, 0 oder mit den Ziffern 3, 2 , 0 erreicht werden. Mit der Ziffer 4 erreichen wir den grösseren Wert! Reihenfolge von hinten

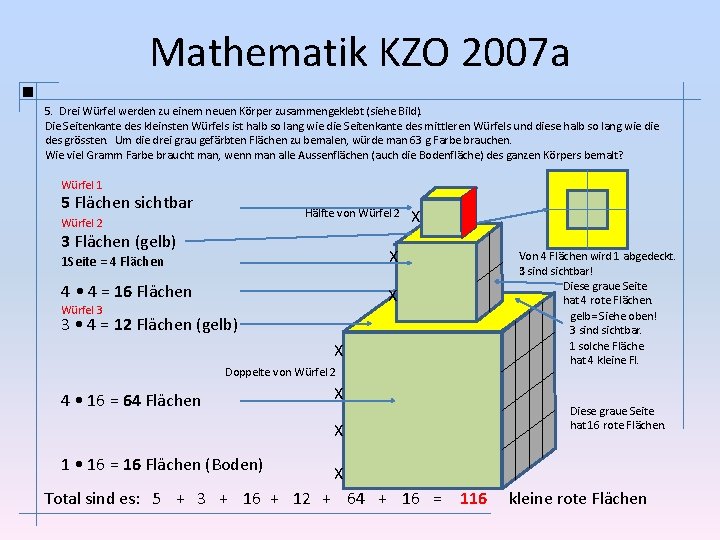
Mathematik KZO 2007 a 5. Drei Würfel werden zu einem neuen Körper zusammengeklebt (siehe Bild). Die Seitenkante des kleinsten Würfels ist halb so lang wie die Seitenkante des mittleren Würfels und diese halb so lang wie des grössten. Um die drei grau gefärbten Flächen zu bemalen, würde man 63 g Farbe brauchen. Wie viel Gramm Farbe braucht man, wenn man alle Aussenflächen (auch die Bodenfläche) des ganzen Körpers bemalt? Würfel 1 5 Flächen sichtbar Hälfte von Würfel 2 3 Flächen (gelb) 1 Seite = 4 Flächen X 4 • 4 = 16 Flächen X Würfel 3 X 3 • 4 = 12 Flächen (gelb) X Doppelte von Würfel 2 4 • 16 = 64 Flächen X X 1 • 16 = 16 Flächen (Boden) Von 4 Flächen wird 1 abgedeckt. 3 sind sichtbar! Diese graue Seite hat 4 rote Flächen. gelb= Siehe oben! 3 sind sichtbar. 1 solche Fläche hat 4 kleine Fl. Diese graue Seite hat 16 rote Flächen. X Total sind es: 5 + 3 + 16 + 12 + 64 + 16 = 116 kleine rote Flächen

Mathematik KZO 2007 a 5. Drei Würfel werden zu einem neuen Körper zusammengeklebt (siehe Bild). Die Seitenkante des kleinsten Würfels ist halb so lang wie die Seitenkante des mittleren Würfels und diese halb so lang wie des grössten. Um die drei grau gefärbten Flächen zu bemalen, würde man 63 g Farbe brauchen. Wie viel Gramm Farbe braucht man, wenn man alle Aussenflächen (auch die Bodenfläche) des ganzen Körpers bemalt? Total sind es: 116 kleine rote Flächen Die grauen Seiten haben: 1 + 4 + 16 = 21 kleine rote Flächen 21 kl. rote Fl. : 21 • 116 brauchen 63 g Farbe 21 r. Fl. 63 g Farbe 116 r. Fl. 348 g Farbe 1 r. Fl. 3 g Farbe Man braucht 348 g Farbe. : 21 • 116

Mathematik KZO 2007 a 1. Auto 90 km/h 2. Auto 60 km/h Unterschied: 30 km/h 9: 50 Uhr A 20 km Unterschied zwischen 90 km/h und 60 k/h : 5 • 2 60 min 24 min 12 min = 30 km/h 30 km 12 km 6 km Nach 24 min beträgt der Unterschied 12 km. : 5 • 2 9: 50 Uhr 6. Zwei Autos fahren von A nach B. Sie starten gleichzeitig in A. Das eine Auto fährt mit einer durchschnittlichen Geschwindigkeit von 90 km/h, das andere mit 60 km/h. Um 9. 50 Uhr ist das schnellere Auto noch 3 km, das langsamere noch 20 km von B entfernt. a) Wie gross ist der Abstand der beiden Autos nach 24 Minuten? 12 km b) Um welche Zeit sind die beiden Autos gestartet? B 3 km

Mathematik KZO 2007 a 2. Auto 90 km/h 60 km/h 34 min Unterschied: 30 km/h Unterschied von 9: 50 Uhr zwischen Auto 1 und 2 bis B: Der Unterschied in 30 min beträgt 17 km In 1 h sind das: Wie lang braucht es für 34 km? 9: 50 Uhr • 2 30 min 60 min Unterschied: 17 km 20 km 9: 50 Uhr 1. Auto 9: 16 Uhr A 20 km 17 km 34 km B 3 km = 17 km • 2 60 min : 60 60 km 34 min • 34 1 km 1 min • 34 34 min = 9: 16 Uhr Die Autos sind um 9: 16 Uhr gestartet. 9: 50 Uhr 6. Zwei Autos fahren von A nach B. Sie starten gleichzeitig in A. Das eine Auto fährt mit einer durchschnittlichen Geschwindigkeit von 90 km/h, das andere mit 60 km/h. Um 9. 50 Uhr ist das schnellere Auto noch 3 km, das langsamere noch 20 km von B entfernt. a) Wie gross ist der Abstand der beiden Autos nach 24 Minuten? b) Um welche Zeit sind die beiden Autos gestartet? Beim Auto 2 sind 30 km/h Unterschied genau 30 min Einfacher mit überlegen. Auto 2 braucht pro 1 km genau 1 min! Für 34 km braucht es daher 34 min.

Mathematik KZO 2007 a 7. Bauer Hürlimann hat 14 Pferde und 17 Kühe im Stall. Eine Kuh frisst doppelt so viel Heu wie ein Pferd. Der Heuvorrat von Bauer Hürlimann würde für 110 Tage reichen. Nach 30 Tagen nimmt der Bauer zusätzlich sechs Kühe in seinen Stall auf. Wie lange reicht der Heuvorrat insgesamt? 48 (gleich viel fressende) Tiere 14 Pferde + 34 „Kühe“ (2 x 17= K. ) Für 48 Tiere reicht der Vorrat 110 Tage. 6 Kühe = 12 Tiere 48 T. 80 d 64 d 30 d 110 d - 30 d = 80 d Die 48 Kühe könnten noch 80 d fressen. Nach 30 d kommen 12 Tiere dazu. Es sind neu 60 T. Wie lang können jetzt die 60 T. fressen? : 4 • 5 48 T. 80 d 60 T. 64 d 12 T. 320 d • 4 : 5 Dauer bis zu den zusätzlichen Tieren: 30 d Dauer mit den zusätzlichen Tieren: 64 d Insgesamt dauert der Heuvorrat = 94 d 60 T. 110 d = 94 d Je weniger Tiere fressen, desto länger reicht der Vorrat. (indirekt) = 94 d

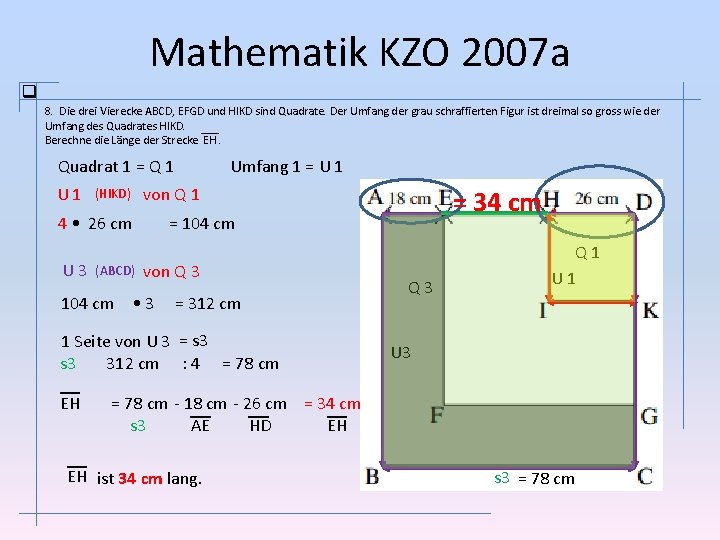
Mathematik KZO 2007 a 8. Die drei Vierecke ABCD, EFGD und HIKD sind Quadrate. Der Umfang der grau schraffierten Figur ist dreimal so gross wie der Umfang des Quadrates HIKD. Berechne die Länge der Strecke EH. Quadrat 1 = Q 1 U 1 (HIKD) von Q 1 4 • 26 cm U 3 (ABCD) Umfang 1 = U 1 = 104 cm von Q 3 104 cm • 3 = 312 cm 1 Seite von U 3 = s 3 312 cm : 4 = 78 cm EH = 34 cm Q 3 Q 1 U 3 = 78 cm - 18 cm - 26 cm = 34 cm EH AE HD s 3 EH ist 34 cm lang. s 3 = 78 cm