Warm up True false If false explain why

Warm – up True / false : If false, explain why • • Collinear points are coplanar Planes have edges Two planes intersect in a line segment Two intersecting lines meet in exactly one point • Line XY can be denoted as XY or YX. • A line has one endpoint

1. 3 Segments, Rays, and Distance

• Segment – Is the part of a line consisting of two endpoints & all the points between them. – Notation: 2 capital letters with a line over them. – Ex: AB – No arrows on the end of a line. – Reads: Line segment (or segment) AB A B

• Ray – Is the part of a line consisting of one endpoint & all the points of the line on one side of the endpoint. – Notation: 2 capital letters with a line with an arrow on one end of it. Endpoint always comes first. – Ex: AB – Reads: Ray AB – The ray continues on past B indefinitely A B B A

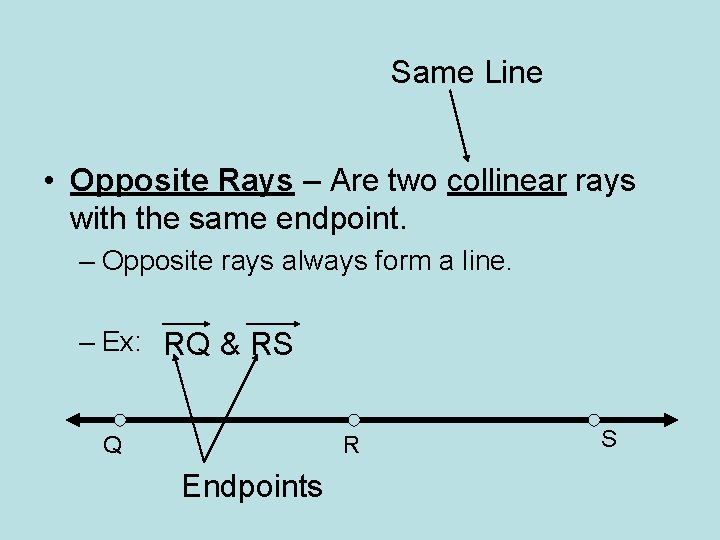
Same Line • Opposite Rays – Are two collinear rays with the same endpoint. – Opposite rays always form a line. – Ex: RQ & RS Q R Endpoints S

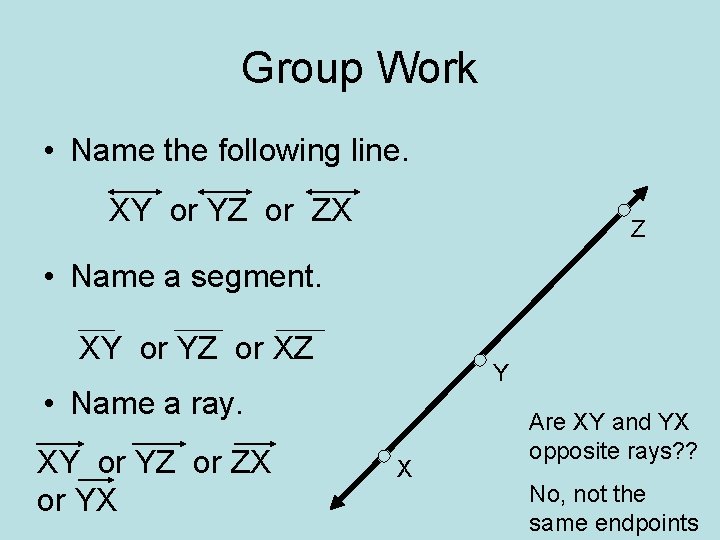
Group Work • Name the following line. XY or YZ or ZX Z • Name a segment. XY or YZ or XZ Y • Name a ray. XY or YZ or ZX or YX X Are XY and YX opposite rays? ? No, not the same endpoints

Number Lines • On a number line every point (LETTER) is paired with a coordinate (NUMBER) – What is the coordinate of each letter? K M J

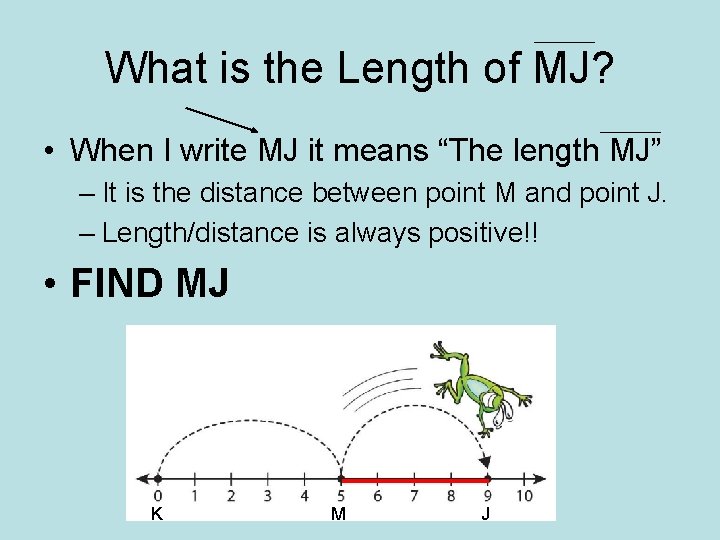
What is the Length of MJ? • When I write MJ it means “The length MJ” – It is the distance between point M and point J. – Length/distance is always positive!! • FIND MJ K M J

Questions 1 -9 -

Congruent • In Geometry, two objects that have – The same size and – The same shape are called congruent. – What are some objects in the classroom that are congruent? – Congruent markings for segments and angles

Congruent Segments • Have equal lengths • To say that DE and FG have equal lengths DE = FG • To say that DE and FG are congruent DE FG 2 ways to say the exact same thing

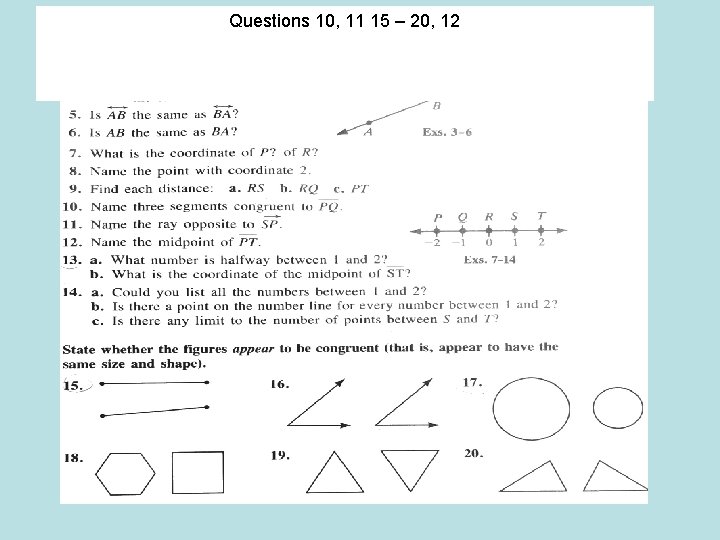
Questions 10, 11 15 – 20, 12

Definition: Midpoint of a segment • Based on the diagram, what does this mean? • The point that divides the segment into two congruent segments. 3 3 B P A What marking do we use to show congruent segments?

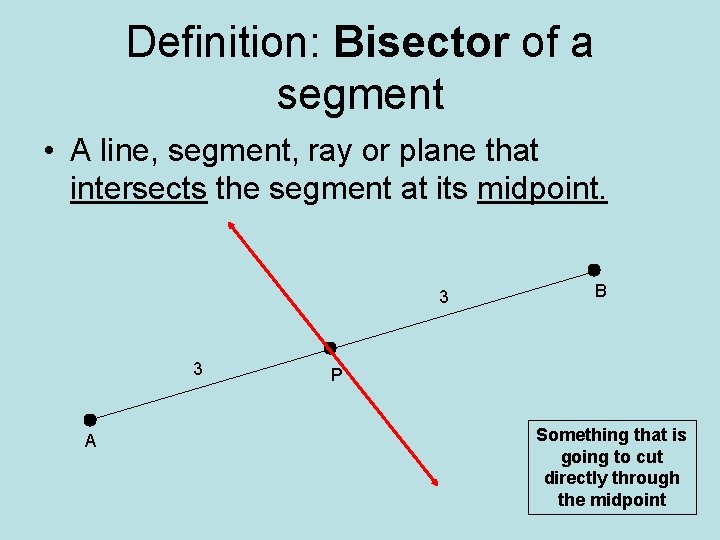
Definition: Bisector of a segment • A line, segment, ray or plane that intersects the segment at its midpoint. 3 3 A B P Something that is going to cut directly through the midpoint

Marking diagram with given information • P. 15 – problems 5 – 18 • P. 16 – 33 - 36

Postulates • Statements that are accepted without proof – They are true and always will be true – They are used in helping to prove further Geometry problems, theorems…. . • Learn them! – Unless it has a name (i. e. “Ruler Postulate”) – Not “Postulate 6” • named different in every text book

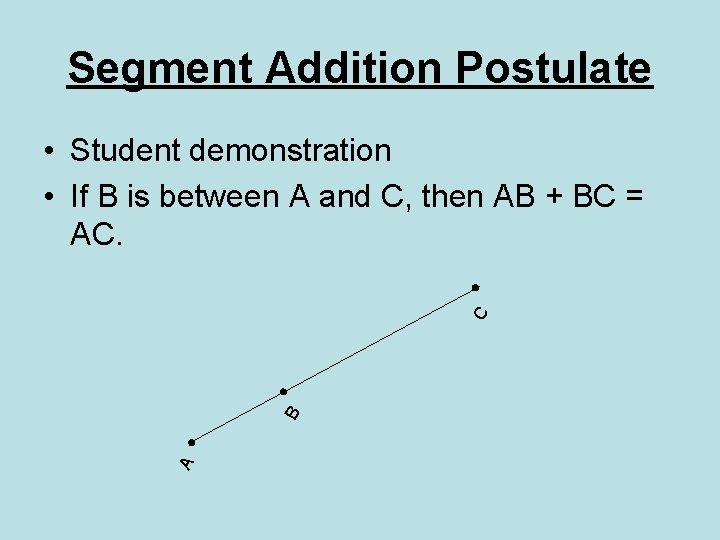
Segment Addition Postulate A B C • Student demonstration • If B is between A and C, then AB + BC = AC.

Example 1 • Use the rule for segment addition postulate to set up an equation A B Write out the problem based on the segments, then substitute in the info C

Example 2 • Use the rule for midpoint to set up an equation – B is the midpoint of segment AC A B C

A- Sometimes B – Always C - Never • A bisector of a segment is ______ a line. • A ray _______ has a midpoint. • Congruent segments ____ have equal lengths. • AB and BA _______ denote the same ray.

Ch. 1 Quiz Know the following… 1. Definition of equidistant 2. Real world example of points, lines, planes 3. Types of intersections (drawings) 4. Points, lines, planes 1. Characteristics 2. Mathematical notation