Timsort Uses Natural mergesort Takes advantage of existing

Timsort

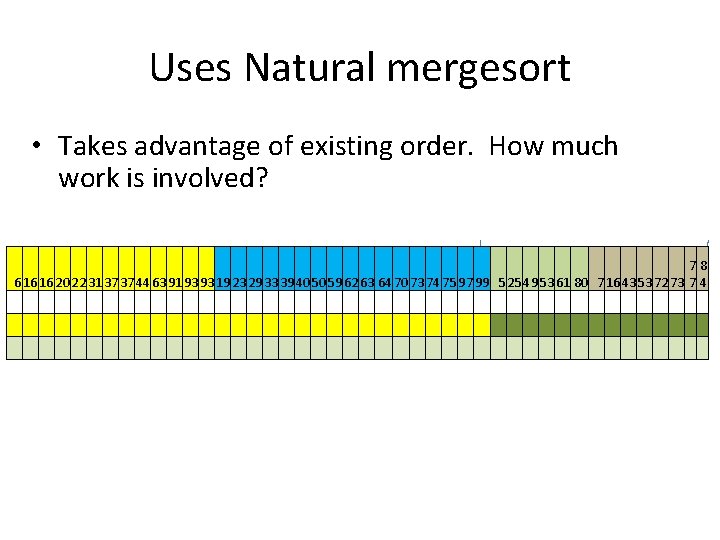
Uses Natural mergesort • Takes advantage of existing order. How much work is involved? 78 6 16 16 20 22 31 37 37 44 63 91 93 93 19 23 29 33 39 40 50 59 62 63 64 70 73 74 75 97 99 5 25 49 53 61 80 7 16 43 53 72 73 7 4

Uses Natural mergesort • Takes advantage of existing order. • Want to take advantage of values that are in memory. That won’t happen if entire array is sorted by adjacent runs log R times (where R is number of runs) • If lots of small runs, what happens to run time? • Height of “work block” is not dependent on n. 16 16 20 22 31 37 37 44 63 91 93 93 19 23 29 33 11 40 50 20 62 63 64 1 73 50 75 97 99 5 25 15 53 61 80 7 16 43 53 72 73 77

Min. Run • If runs are too small, increase the size by using Insertion Sort on small pieces. • For files less than 64, minrun is just 64. We do just a single insertion sort. 16 16 20 22 31 37 37 44 63 91 93 93 19 23 29 33 11 40 50 20 62 63 64 1 73 50 75 97 99 5 25 15 53 61 80 7 16 43 53 72 73 77 16 16 20 22 31 37 37 44 63 91 93 93 11 19 23 29 33 40 50 1 20 62 63 64 73 50 5 25 15 53 75 97 99 7 16 43 53 61 72 73 77 80

Uses Natural mergesort Takes advantage of existing order If we wanted to decrease total run time, what order would we merge the pieces below? What if some pieces weren’t merged as many times as other pieces? Regular Way Modified order

Uses Natural mergesort Takes advantage of existing order If we wanted to decrease total run time, what order would we merge the pieces below? What if some pieces weren’t merged as many times as other pieces? Regular Way Modified order

Require the rules In order to balance run lengths (while keeping a low bound on the number of runs) we maintain two invariants on the stack entries, where A, B and C are the lengths of the three rightmost notyet merged slices: • 1. |A |> |B|+|C| (if not, merge B with the smaller of A and C) • 2. |B| > |C| (if not, merge A and B)

Require the rules • 1. |A |> |B|+|C| (if not, merge B with the smaller of A and C) • 2. |B| > |C| (if not, merge A and B) • What would you do if these were the sizes of the runs: 4 1 5 3 6 11 4 1 13 2 6 2 21 5 3 5

Inverted Order • What if we get a section that is in inverse order? 6 16 16 20 22 31 37 37 44 63 91 93 93 99 97 75 73 70 63 62 50 39 33 22 20 13 11 1 2 4 5 25 49 53 61 6 16 16 20 22 31 37 37 44 63 91 93 93 99 1 11 13 20 22 33 39 50 62 63 70 73 75 97 2 4 5 25 49 53 61 • Why would we need to insist on strictly decreasing order?

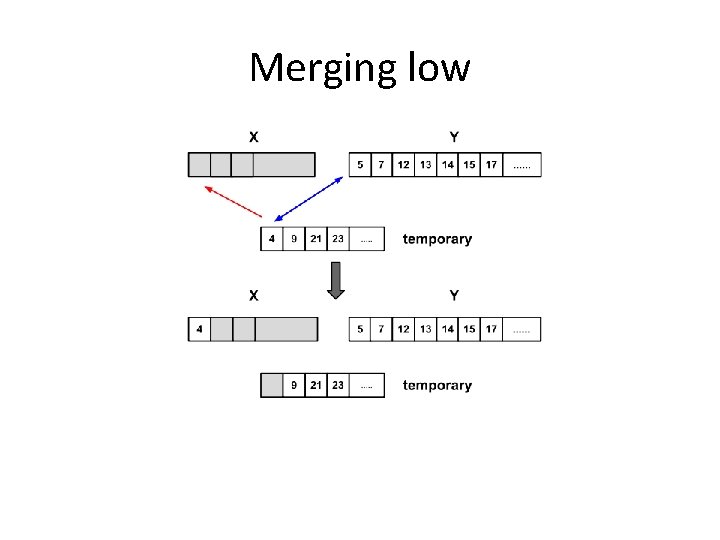
Merging adjacent runs of lengths A and B in-place is very difficult, but if we have temp memory equal to min(|A|, |B|), it's easy. If A is the smaller-sized chunk (function merge_low), copy A to a temp array, leave B alone, and then we can do the obvious merge algorithm left to right. There's always a free area in the original area equal to the number not yet merged from the temp array. In this case a binary search examines A to find the first position larger than the first element of B (a'). Note that A and B are already sorted individually. When a' is found, the algorithm can ignore elements before that position while inserting B. Similarly, the algorithm also looks for the smallest element in B (b') greater than the largest element in A (a). The elements after b' can also be ignored for the merging. 14 16 31 34 35 37 38 41 44 46 50 57 28 30 33 36 40 41 42 48 49 61 62 65

Merging low

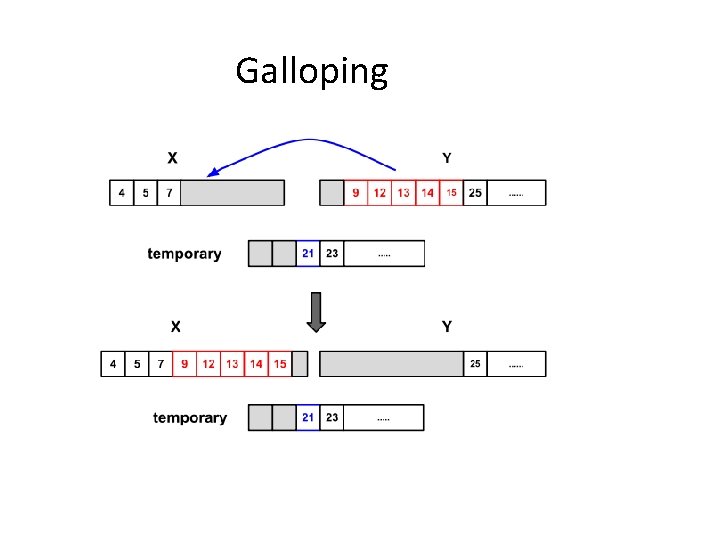
Galloping • Assume A is the shorter run. We enter galloping mode when we keep taking elements from B. In galloping mode, we first look for A[0] in B (using a modified binary search). We do this via "galloping by powers of two", comparing A[0] in turn to B[0], B[1], B[3], B[7], . . . , B[2**j - 1], . . . , until finding the k such that B[2**(k-1) - 1] < A[0] <= B[2**k - 1]. This takes at most roughly lg(|B|) comparisons, and, unlike a straight binary search, favors finding the right spot (which is likely early in B).

Galloping