TALES Z MILETU Maria Usarz kl I a

TALES Z MILETU Maria Usarz kl. I a Justyna Helizanowicz kl. III a

Charakterystyka • Tales z Miletu uważany jest za jednego z "siedmiu mędrców" czasów antycznych i za ojca nauki greckiej. Wbrew legendom mędrzec ów należał do ludzi praktycznych, utrzymywał ożywione stosunki handlowe z Egiptem. To było powodem, iż do krajów tych odbywał częste podróże. I prawdopodobnie wtedy zapoznał się z osiągnięciami matematyki i astronomii Egiptu i Babilonii.

Twierdzenie • Pod najbardziej znanym twierdzeniem Talesowi z Miletu przypisuje się autorstwo: • • • * dowodu, że średnica dzieli koło na połowy; * odkrycia, że kąty przypodstawne w trójkącie równoramiennym są sobie równe; * twierdzenia o równości kątów wierzchołkowych; * twierdzenia o przystawaniu trójkątów o równym boku i przyległych dwu kątach; * twierdzenia, że średnica koła jest widoczna z punktu leżącego na okręgu pod kątemprostym

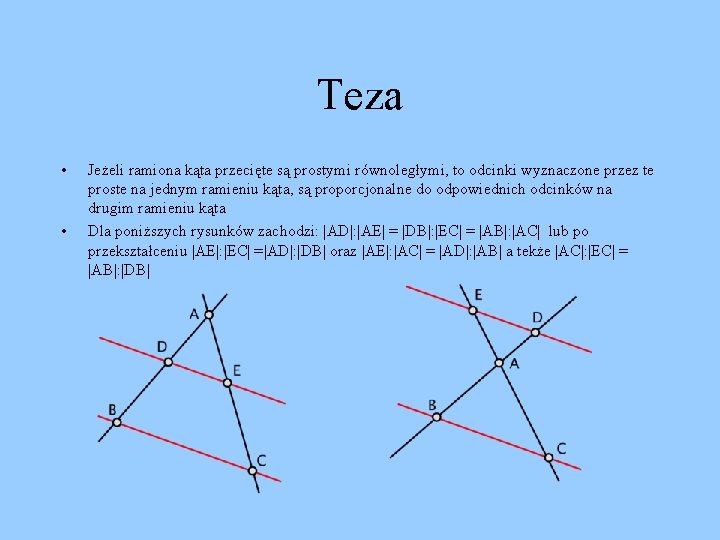
Teza • • Jeżeli ramiona kąta przecięte są prostymi równoległymi, to odcinki wyznaczone przez te proste na jednym ramieniu kąta, są proporcjonalne do odpowiednich odcinków na drugim ramieniu kąta Dla poniższych rysunków zachodzi: |AD|: |AE| = |DB|: |EC| = |AB|: |AC| lub po przekształceniu |AE|: |EC| =|AD|: |DB| oraz |AE|: |AC| = |AD|: |AB| a tekże |AC|: |EC| = |AB|: |DB|

Dowód • • Dowód oparty jest na dwóch lematach: * Lemat I. Jeśli dwa trójkąty mają równe wysokości, to stosunek ich pól jest równy stosunkowi długości ich podstaw. * Lemat II. Jeśli dwa trójkąty mają wspólną podstawę i równe wysokości, to ich pola są równe. 1. Trójkąty CED i EAD mają wspólną wysokość h', więc na mocy lematu I. : |CE|: |EA|=S(CED): S(EAD) 2. Trójkąty CED i BDE mają wspólną podstawę ED i równe wysokości h, więc na mocy lematu II. : S(CED)=S(BDE) stąd: S(CED): S(EAD)=S(BDE): S(EAD) 3. Trójkąty BDE i EAD ma wspólną wysokość, więc na mocy lematu I. : S(BDE): S(EAD)=|BD|: |DA| Łącząc w jeden zapis otrzymujemy: |CE|: |EA|=S(CAD): S(EAD)=S(BDE): S(EAD)=|BD: |DA|

ODKRYCIE MATEMATYCZNE • Tales uchodzi za pierwszego matematyka, który wprowadził do Grecji geometrię, przyswoiwszy sobie jej zasady w czasie pobytu w Egipcie. Przypisuje mu się następujące twierdzenia: • 1) o przepołowieniu koła przez średnicę, • 2) dwa kąty przy podstawie trójkąta równoramiennego są równe, • 3) jeżeli dwie linie proste przecinają się, przeciwległe kąty są równe, • 4) kąt wpisany w półkole jest kątem prostym, • 5) trójkąt jest określony, jeżeli dana jest jego podstawa i kąty przy podstawie. • Twierdzenia 1 -3 przypisywał Talesowi Proklos, powołując się na autorytet Eudemosa. Twierdzenie 4 jest przytoczone przez Diogenesa Laertiosa wraz z informacją, że po wpisaniu trójkąta prostokątnego w koło, Tales złożył bogom wołu w ofierze. Twierdzenie 5 wiąże się z pomiarami odległości okrętów na morzu, ale zarówno to twierdzenie, jak i pomiary wysokości piramid przy pomocy ich cienia, mogły być przeprowadzone w sposób czysto empiryczny, bez odwoływania się do praw geometrii.