Tales z Miletu filozof uczony grecki przedstawiciel joskiej

Tales z Miletu – filozof (uczony) grecki przedstawiciel jońskiej filozofii przyrody. Powszechnie uznawany za pierwszego filozofa cywilizacji zachodniej oraz za inicjatora badań nad przyrodą jako nauki. Należy też do kanonu siedmiu mędrców. Grecy widzieli w nim jednak raczej mędrca, niż filozofa.

Główne tezy filozoficzne przypisywane Talesowi (omówione szczegółowo w kolejnych rozdziałach) to: � Zasadą jest woda � Magnes posiada duszę � Wszystko jest pełne bogów � Dusze są nieśmiertelne

� � � � Człowieka ocenia się wedle pieniędzy: nikt, kto biedny, nie cieszy się szacunkiem. Dla cierpiącego fizycznie potrzebny jest lekarz, dla cierpiącego psychicznie – przyjaciel. Dlaczego nie mam dzieci? Z miłości do dzieci! Dobroć jest jak rosa, która poi spragnionych. Dusza człowieka jest odzwierciedleniem nieskażonej, czystej wody. Gadulstwo nigdy nie zwiastuje rozumnej myśli. Jak ty rodzicom, tak dzieci tobie. Kropla drąży skałę. Księżyc pożycza światło od słońca. Lekarstwem dla chorej duszy jest dobre słowo. Ludzi jest wielu, mędrców mało. Nadzieją w ostatniej godzinie jest dla człowieka myśl, że więcej nie będzie musiał się narodzić. Najdziwniejszą rzeczą, jaką w życiu widziałem, był stary tyran.

Zgodnie z przekazami starożytnych, a w szczególności greckiego filozofa Proklosa, żyjącego w V w. p. n. e. , Talesowi przypisuje się następujące twierdzenia geometryczne: 1. Średnica dzieli okrąg na połowy. 2. Dwa kąty przy podstawie trójkąta równoramiennego są równe. 3. Kąty wierzchołkowe, powstałe na skutek przecięcia dwóch linii prostych są równe. 4. Kąt wpisany w okrąg i oparty na jego średnicy jest kątem prostym. 5. Jeżeli w dwóch trójkątach bok i przyległe do niego kąty są równe, to te trójkąty są przystające.

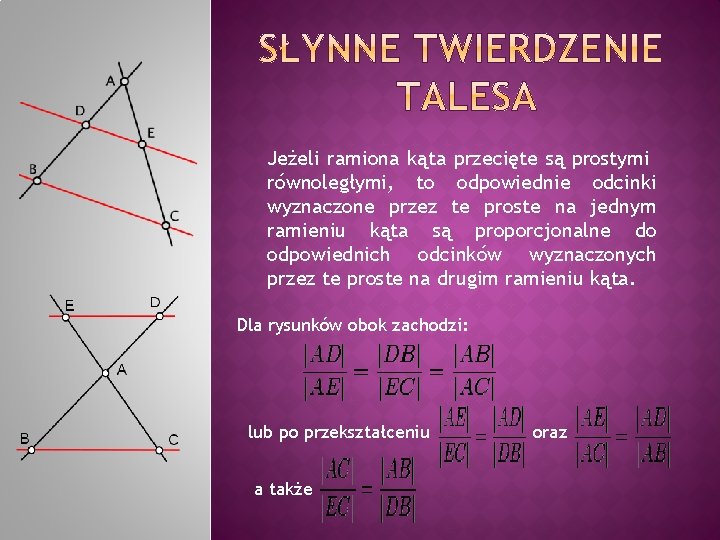
Jeżeli ramiona kąta przecięte są prostymi równoległymi, to odpowiednie odcinki wyznaczone przez te proste na jednym ramieniu kąta są proporcjonalne do odpowiednich odcinków wyznaczonych przez te proste na drugim ramieniu kąta. Dla rysunków obok zachodzi: lub po przekształceniu a także oraz

Figury, mające ten sam kształt, a różniące się co najwyżej wielkością, nazywamy figurami podobnymi.

I cecha II cecha Jeżeli dwa trójkąty prostokątne mają po jednym kącie ostrym przystającym, to te trójkąty są podobne. Jeżeli stosunek długości przyprostokątnych jednego trójkąta jest równy stosunkowi długości przyprostokątnych drugiego trójkąta, to te trójkąty są podobne. . α 1 = α lub β 1 = β

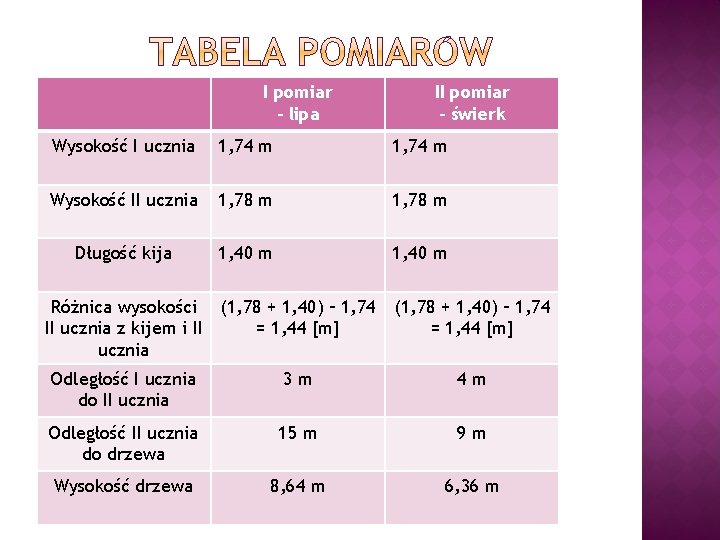
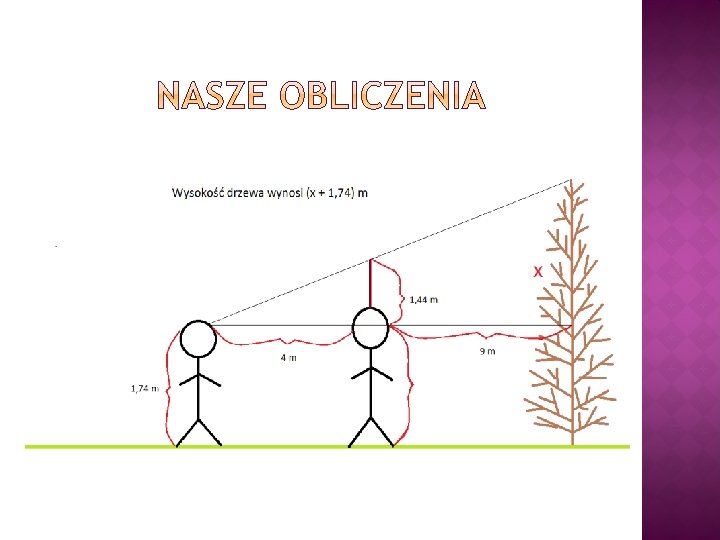
I pomiar - lipa II pomiar - świerk Wysokość I ucznia 1, 74 m Wysokość II ucznia 1, 78 m Długość kija 1, 40 m Różnica wysokości (1, 78 + 1, 40) – 1, 74 II ucznia z kijem i II = 1, 44 [m] ucznia (1, 78 + 1, 40) – 1, 74 = 1, 44 [m] Odległość I ucznia do II ucznia 3 m 4 m Odległość II ucznia do drzewa 15 m 9 m Wysokość drzewa 8, 64 m 6, 36 m

Małgorzata Śmietana – lider Kamil Pustuł Monika Wójcik Mikołaj Wnuk Wiktoria Zaborska Pod kierunkiem mgr Elżbiety Węgrzyniak