System Optimization II Multidisciplinary Design Optimization K Sudhakar



















- Slides: 23

System Optimization - II Multi-disciplinary Design Optimization K Sudhakar PM Mujumdar Centre for Aerospace Systems Design & Engineering Indian Institute of Technology, Mumbai June-July, 2003 IAT, Pune 1

Objective Function(s) If maximisation is required ie, Maximise f(x) then restate it as Minimise F(x) = -f (x) June-July, 2003 IAT, Pune 2

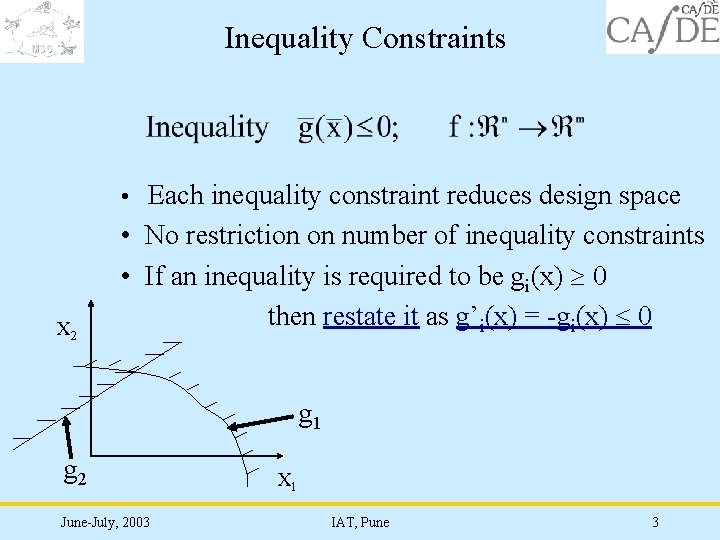
Inequality Constraints • Each inequality constraint reduces design space X 2 • No restriction on number of inequality constraints • If an inequality is required to be gi(x) 0 then restate it as g’i(x) = -gi(x) 0 g 1 g 2 June-July, 2003 X 1 IAT, Pune 3

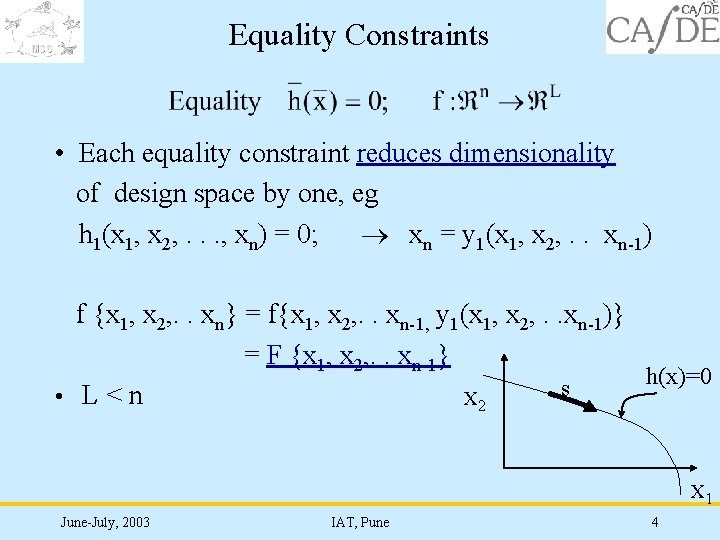
Equality Constraints • Each equality constraint reduces dimensionality of design space by one, eg h 1(x 1, x 2, . . . , xn) = 0; xn = y 1(x 1, x 2, . . xn-1) f {x 1, x 2, . . xn} = f{x 1, x 2, . . xn-1, y 1(x 1, x 2, . . xn-1)} = F {x 1, x 2, . . xn-1} h(x)=0 s • L<n X 2 X 1 June-July, 2003 IAT, Pune 4

Optimization Problem Statement n 1 • Side constraints • Boxing design space • Bounding box n - Independant variables L - Equality constraints; m - Inequality constraints June-July, 2003 f IAT, Pune 5

Engineering Design • Parameterize - identify variables, which if given values, design is realizable. {b, C_r, S, , , a/f, VH, VV. . } • Identify analysis to determine feasibility compliance with customer requirements. ie. Evaluate all constraints • Identify goodness criteria • Optimize June-July, 2003 IAT, Pune 6

Constraints • Customer needs are constraints g = {Range, Vmax, ROC, . , OEI, . , noise, . . }; g m These are usually inequality constraints, gi 0 • Laws of nature that cannot be violated are constraints h = {Newton’s laws, conservation laws, . }; h L These are usually equality constraints, h = 0. June-July, 2003 IAT, Pune 7

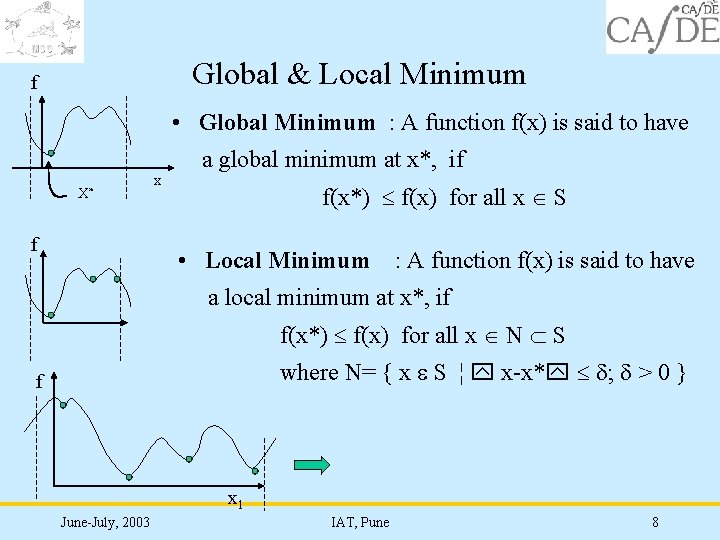
Global & Local Minimum f • Global Minimum : A function f(x) is said to have a global minimum at x*, if X* f x f(x*) f(x) for all x S • Local Minimum : A function f(x) is said to have a local minimum at x*, if f(x*) f(x) for all x N S where N= { x S ¦ x-x* ; > 0 } f x 1 June-July, 2003 IAT, Pune 8

1 -D Unconstrained f Minimise f(X) = (x 1 - 2)2 f/ x 1 = 2 (x 1 - 2) ; 2 f/ x 12 = 2 x 1* = 2, f* = 0 ; x 1 Point of minima Some points for consideration! • f - Simple function, easy to analytically differentiate. • What if f is complex? Numerically differentiate? X 1 June-July, 2003 IAT, Pune Computer Programme f 9

n-D Unconstrained • Solve the n equations for x 1, x 2 , x 3. . . xn • Check for Positive definiteness of H. All eigenvalues of H should be 0 June-July, 2003 IAT, Pune 10

Two Variable Problem Minimise f(X) = (x 1 - 2)2 + (x 2 - 2)2 Tf = [ f/ x 1 ; f/ x 2 ] = [ 2(x 1 - 2) ; 2(x 2 - 2) ] 2 f/ x 12 2 f/ x 1 x 2 H(f) = 2 0 0 2 = 2 f/ x 2 x 1 X* = ( 2, 2); 2 f/ x 22 f* = 0; Point of minima, since H +ve Definite ( 1 = 2) June-July, 2003 IAT, Pune 11

Equality Constrained Minima Minimise Subject to f (x 1, x 2, x 3) h (x 1, x 2 , x 3) = 0 Solve for x 1 = (x 2 , x 3) Minimise f ( (x 2 , x 3), x 2 , x 3) = F (x 2 , x 3) What if h (x 1, x 2 , x 3) cannot be explicitly inverted? X 1 , X 2 , X 3 June-July, 2003 IAT, Pune Computer Programme h 12

Equality Constrained Minima Minimise f(x 1, x 2); Subject to h(x 1, x 2) = 0 Is equivalent to the un-constraint problem Minimise L(x 1, x 2, ) = f(x 1, x 2) + h(x 1, x 2) L/ x 1 = f/ x 1 + h/ x 1 = 0 L/ x 2 = f/ x 2 + h/ x 2 = 0 L/ = h = 0 - Lagrange multiplier June-July, 2003 IAT, Pune 13

Constrained Optimisation Inequality Constraints g 1=0 x 2 g 1= -s 2 X* x 1 - Lagrange multiplier; June-July, 2003 IAT, Pune s - slack variable 14

Constrained Optimisation June-July, 2003 IAT, Pune 15

Issues in Posing the Problem • Of all variables that influence the design which to pick as design variables? XD X • Of all functions that determine system behaviour which one to choose as objectives? f F • How to confirm that all constraints are specified ? • How to evaluate f, g, h ? June-July, 2003 IAT, Pune 16

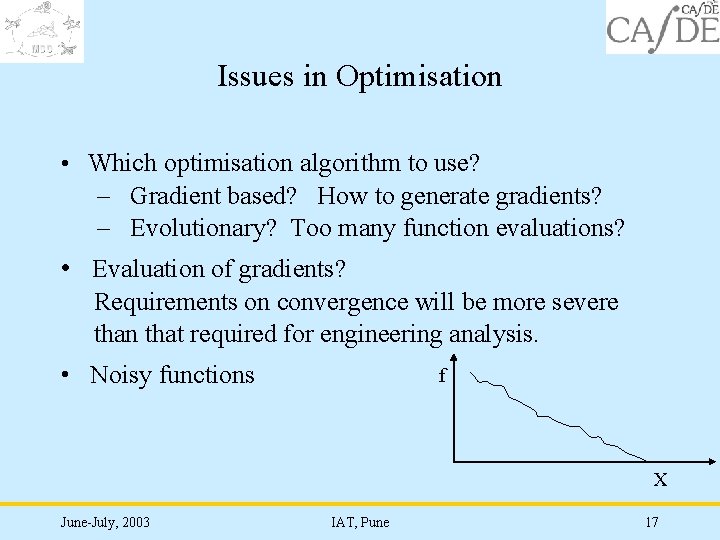
Issues in Optimisation • Which optimisation algorithm to use? – Gradient based? How to generate gradients? – Evolutionary? Too many function evaluations? • Evaluation of gradients? Requirements on convergence will be more severe than that required for engineering analysis. • Noisy functions f X June-July, 2003 IAT, Pune 17

Issues in Optimisation • Special issues in large scale problems? Experience of others? • Issues when strong inter-disciplinary interactions exist - especially when disciplinary analysis is complex. • Intensive, complex legacy codes for analysis • Are there environments that make problem posing and problem solving easy. June-July, 2003 IAT, Pune 18

• To know more about CASDE http: //www. casde. iitb. ac. in • To know more about MDO work at CASDE http: //www. casde. iitb. ac. in/MDO/ • To contact me sudhakar@aero. iitb. ac. in June-July, 2003 IAT, Pune 19

Thank you June-July, 2003 IAT, Pune 20

Customer Requirements • • Mach no. M 0. 8 ( -M -0. 8) ROC 100 m/s (-ROC -100 m/s) Take off distance, TOD 800 m Noise level 90 EPNDB • . . June-July, 2003 IAT, Pune 21

Conservation Principles, etc • Mass is conserved, Menrty - Mexit = 0 • Linear momentum is conserved, T - D - m d. V/dt = 0 (for accelerated flight) L-W = 0 (for 1 -g level flight) • . . June-July, 2003 IAT, Pune 22

Multi-modal Function June-July, 2003 IAT, Pune 23
 Sudhakar patra
Sudhakar patra Sudhakar prasad
Sudhakar prasad Digital banking platform
Digital banking platform Sudhakar patra
Sudhakar patra Sudhakar rao nirupama rao
Sudhakar rao nirupama rao Multidisciplinary nature of environmental studies;
Multidisciplinary nature of environmental studies; Multidisciplinary team pros and cons
Multidisciplinary team pros and cons Temasek laboratories
Temasek laboratories Multidisciplinary vs interdisciplinary
Multidisciplinary vs interdisciplinary Multidisciplinary vs interdisciplinary
Multidisciplinary vs interdisciplinary Multidisciplinary nature of environmental studies ppt
Multidisciplinary nature of environmental studies ppt Multidisciplinary engineering definition
Multidisciplinary engineering definition Conflict in multidisciplinary teams
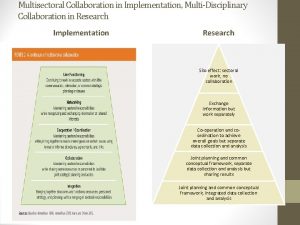
Conflict in multidisciplinary teams Multisectoral and multidisciplinary
Multisectoral and multidisciplinary Interdisciplinary multidisciplinary transdisciplinary
Interdisciplinary multidisciplinary transdisciplinary Epcc degree plans
Epcc degree plans Network design and optimization
Network design and optimization Numerical optimization techniques for engineering design
Numerical optimization techniques for engineering design Machine independent assembler features tutorialspoint
Machine independent assembler features tutorialspoint Systems and forms design
Systems and forms design User interface design in system analysis and design
User interface design in system analysis and design Dialogue design
Dialogue design Properties of a system in system analysis and design
Properties of a system in system analysis and design System security in system analysis and design
System security in system analysis and design