SwitchSetting Games Torsten Muetze Content Introduction n General

Switch-Setting Games Torsten Muetze

Content Introduction n General theory n Case study n

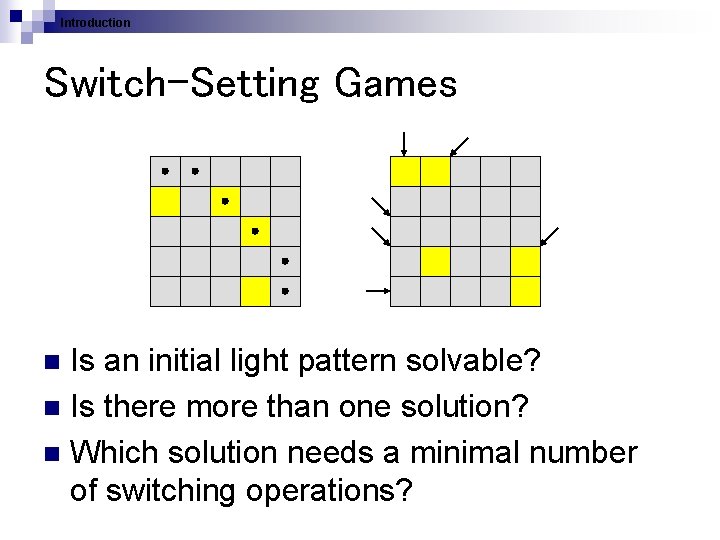
Introduction Switch-Setting Games Is an initial light pattern solvable? n Is there more than one solution? n Which solution needs a minimal number of switching operations? n

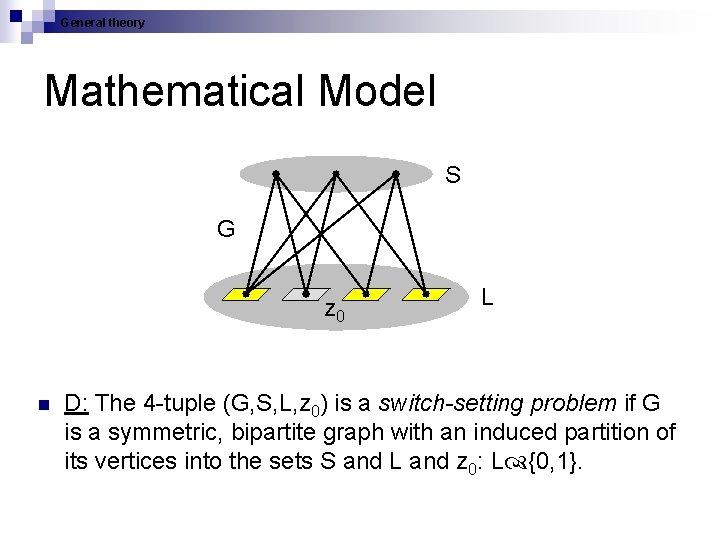
General theory Mathematical Model S G z 0 n L D: The 4 -tuple (G, S, L, z 0) is a switch-setting problem if G is a symmetric, bipartite graph with an induced partition of its vertices into the sets S and L and z 0: L {0, 1}.

General theory Solution Behavior s 1 l 1 s 2 l 2 0 s 3 l 3 AS, L A= z 0 l 4 AL, S s 1 s 2 s 3 0 l 1 1 1 l 2 1 1 0 0 1 l 3 1 0 1 1 0 l 4 0 1 1 1 0 AL, ST = AS, L AL s 2 sequence of switches s‘ 0, s‘ 1, . . . , s‘k S 5 z 0 + AL, S s‘ 1 +. . . + AL, S s‘k = 0 (mod 2) z 0 + AL, S ( s‘ 0 + s‘ 1 +. . . + s‘k) = 0 (mod 2) =: x AL, S z 0 + , S 5 {0, 1} S AL, S x = z 0 (mod 2) solvability: ker(AL, ST) all solutions: ker(AL, S) (AL, ST = AS, L)

General theory Parity Domination n S D: Even L-dominating set X 4 S : 5 X N(l) has even cardinality for all l L. n X L AL, S x = 0 (mod 2) Even S-dominating set Z 4 L : 5 S Z N(s) has even cardinality for all s S. Z L AS, L z = 0 (mod 2) n T: X 4 S is an even L-dominating set 5 x ker(AL, S). Z 4 L is an even S-dominating set 5 z ker(AS, L).

General theory Main Theorem n T: Let P=(G, S, L, z 0) be a switch-setting problem and A the adjacency matrix of G. The following statements are equivalent: (i) P has a solution. (ii) AL, S x = z 0 (mod 2) has a solution. (iii) For all z ker(AS, L) the relation z. Tz 0 = 0 (mod 2) holds. (iv) For all z from a basis of ker(AS, L) the relation z. Tz 0 = 0 (mod 2) holds. (v) The number of lit lamps on every even S-dominating set is even. (vi) The number of lit lamps on every even S-dominating set from a basis of the set of all even S-dominating sets is even. S S L Z 1 S L Z 2 L Z 1+Z 2

Case study n Rules n Switching operation: toggle all lamps on either a row, a column a diagonal or an antidiagonal n Formal definition of the underlying graph Gm, n = (V, E) m |S| = 3(m+n)-2 |L| = mn G 2, 2 Z={l 1, 1, l 2, 1}4 L X={s*2, s*1}4 S

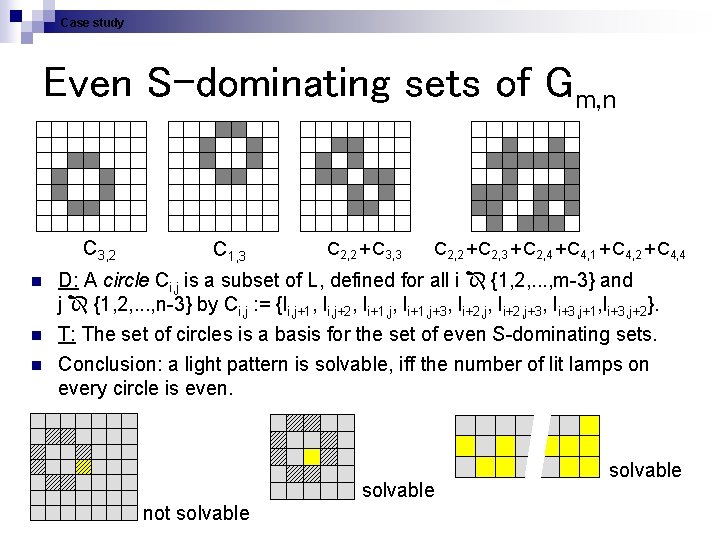
Case study Even S-dominating sets of Gm, n C 3, 2 C 1, 3 C 2, 2 + C 3, 3 C 2, 2 + C 2, 3 + C 2, 4 + C 4, 1 + C 4, 2 + C 4, 4 n D: A circle Ci, j is a subset of L, defined for all i {1, 2, . . . , m-3} and j {1, 2, . . . , n-3} by Ci, j : = {li, j+1, li, j+2, li+1, j+3, li+2, j+3, li+3, j+1, li+3, j+2}. n T: The set of circles is a basis for the set of even S-dominating sets. n Conclusion: a light pattern is solvable, iff the number of lit lamps on every circle is even. solvable not solvable

Case study n Even L-dominating sets of Gm, n For min(m, n)R 4 there always 27=128 even L-dominating sets n A basis for the even L-dominating sets of G 4, 4 n A basis for the even L-dominating sets of Gm, n (min(m, n) 4) X 1 ‘ Problem X 2 ‘ Possible Solutions X 14 X + X 1 ‘ 14 X + X 2 ‘ 11 Minimal solution?

Summary General theory for the mathematical treatment of switch-setting games n Interesting and fruitful relations between concepts from graph theory and linear algebra n Graphically aesthetic interpretations n

References n n n [1] K. Sutner. Linear cellular automata and the garden-of-eden. Math. Intelligencer, 11: 49 -53, 1989. [2] J. Goldwasser, W. Klostermeyer, and H. Ware. Fibonacci polynomials and parity domination in grid graphs. Graphs Combin. , 18: 271 -283, 2002. [3] D. Pelletier. Merlin‘s Magic Square. Amer. Math. Monthly, 94: 143 -150, 1987. [4] M. Anderson and T. Feil. Turning lights out with linear algebra. Math. Magazine, 71: 300 -303, 1998. [5] T. Muetze. Generalized switch-setting problems. Preprint.