Sum of a Linear Array Given an array

Sum of a Linear Array • Given an array a = ( ai: i = 0, 1, …, n – 1 ), compute the sum of its elements: s = a 0 + a 1+…+ an – 1 • Elementary operations: – fetching ai from memory: n operations per array – addition: n – 1 operations per array Lecture 2 COMPSCI. 220. S 1. T - 2004 1

Sum of a Linear Array • Linear computing time: for n >> 1 T(n) c n • Factor c depends on the computer, operating system, programming language, compiler, etc • Linear relative changes: T(a n) = a T(n) Lecture 2 COMPSCI. 220. S 1. T - 2004 2

Sums of Contiguous Subsequences • Given an array (ai: i = 0, 1, …, n – 1) of size n =2 m, compute m + 1 sums: sk = ak + ak+1 + …+ a k+m– 1; k = 0, …, m of all contiguous subsequences of size m • Brute force computation: c m operations per subsequence; in total: c 3 Lecture 2 COMPSCI. 220. S 1. T - 2004 m (m + 1) operations

Sums of Contiguous Subsequences • Brute-force program (two nested loops): . . . int[ ] s = new int[ m + 1 ]; for( int k = 0; k <= m; k++ ) { // m + 1 sums s[ k ] = 0; for( int i = 0; i < m; i++ ) // each sum: c m COMPSCI. 220. S 1. T - 2004 Lecture 2 s[ k ] += a[ k + i ]; // 4

Brute-force Quadratic Approach • Quadratic time (two nested loops): • Quadratic relative changes: Lecture 2 COMPSCI. 220. S 1. T - 2004 5

Brute-force Quadratic Approach • Quadratic time complexity is due to reiterated computations in the innermost loop Lecture 2 COMPSCI. 220. S 1. T - 2004 6

Getting Linear Computing Time • Exclude reiterated computations of the “brute-force” algorithm: • As a result, the linear computing time: Lecture 2 COMPSCI. 220. S 1. T - 2004 7

Getting Linear Computing Time • Better program (two successive loops): . . . int[ ] s new int[ m + 1 ]; s[ 0 ] 0; for( int i 0; i < m; i++ ) // first sum: m operations s[ 0 ] + a[ i ]; for( int k = 1; k <= m; k++ ) // 2 operations per sum s[ k ] = s[ k – 1 ] + a[ k + m – 1] - a[ k – Lecture 2 COMPSCI. 220. S 1. T - 2004 8 1 ];

Computing Time for T(1)=1 ms Array size n Size / number of subsequences Brute-force (quadratic) algorithm Efficient (linear) algorithm Lecture 2 2, 000, 000 m / 1, 000, 000 m + 1 1, 001 / 1, 000, 001 T(n) 2 s > 23 days T(n) 1. 5 ms COMPSCI. 220. S 1. T - 2004 1. 5 s 9

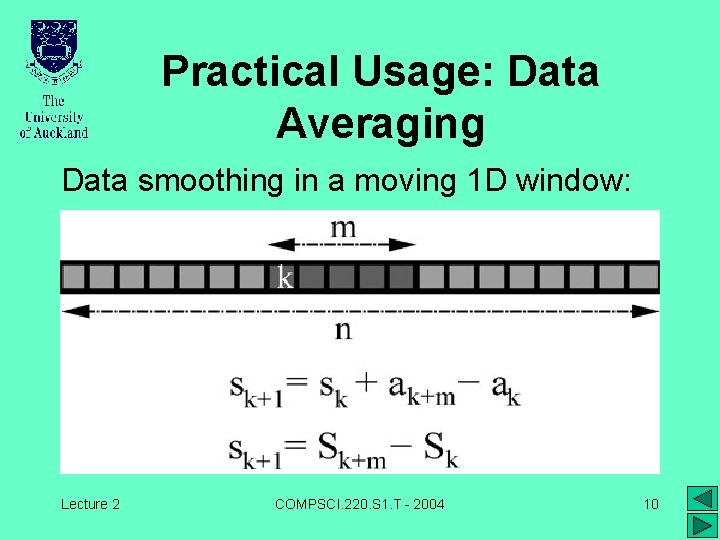
Practical Usage: Data Averaging Data smoothing in a moving 1 D window: Lecture 2 COMPSCI. 220. S 1. T - 2004 10

Data Averaging Window size: m { 2, 3, …, n/2 } Partial sums: Sk = a 0 +. . . + ak Brute-force approach: T(n) c · m · n C · n 2 if m is a fraction of n Brute-force computing time might be even cubic: T(n) C · n 3 when the averaged data should COMPSCI. 220. S 1. T be compared for many 11 Lecture 2 - 2004 windows 2 m n/

Faster Data Averaging • Sequential modification of the current sum: T(n) m + 2·(n - m) per window (m n/2 ) • An extra memory for storing n partial sums Sk = a 0+a 1+…+ak; k = 0, 1, …, n-1 Lecture 2 2004 12 allows to find. COMPSCI. 220. S 1. T the sum- of each

Estimating Running Time • Simplifying assumptions: – all elementary statements / expressions take the same amount of time to execute • e. g. , simple arithmetic assignments • return • Loops increase in time linearly as k Tbody of a loop where k is number of times the loop is executed Lecture 2 COMPSCI. 220. S 1. T - 2004 13

Estimating Running Time • Conditional / switch statements are more complicated (because it is necessary to account for frequencies of branches) • Function calls: Tfunction = S Tstatements in function • Function composition: T(f(g(n))) = T(g(n))+T(f(n)) Lecture 2 COMPSCI. 220. S 1. T - 2004 14

Estimating Running Time • Function calls: T = S Tstatement . . . ){ i . . . x. my. Method( y, . . . ); public void my. Method( int a, statements 1, 2, …, N } • Function composition T(f(g(n))) Computation of x = g(n) T(g(n)) Lecture 2 COMPSCI. 220. S 1. T - 2004 Computation of y = f(x) T(f(n)) 15

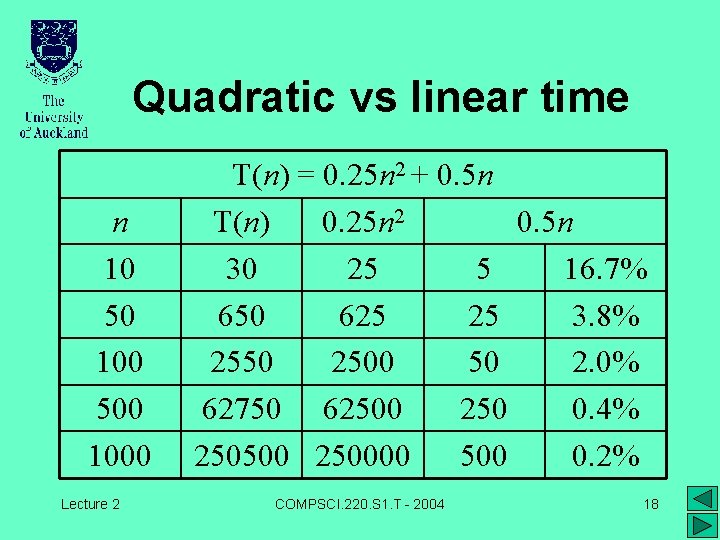
Time to Sum Contiguous Sequences • Ignore data initialisation code • “Brute-force” nested loops: T(n) = m · (m +1) = n/2 · ( n/2 + 1 ) = 0. 25 n 2 + 0. 5 n • For a large n, T(n) 0. 25 n 2 – e. g. , if n > 500, 0. 5 n < 0. 4% of T(n) Lecture 2 COMPSCI. 220. S 1. T - 2004 16

Time to Sum Contiguous Sequences • Factor c = 0. 25 is referred to as a “constant of proportionality” • This factor does not effect the behaviour of the algorithm for a large n: – 10% increase in n leads to a 20% increase in T(n) Lecture 2 COMPSCI. 220. S 1. T - 2004 17

Quadratic vs linear time n 10 50 100 500 1000 Lecture 2 T(n) = 0. 25 n 2 + 0. 5 n T(n) 0. 25 n 2 0. 5 n 30 25 5 16. 7% 650 625 25 3. 8% 2550 2500 50 2. 0% 62750 62500 250 0. 4% 250500 250000 500 0. 2% COMPSCI. 220. S 1. T - 2004 18