Studying cool planets around distant lowmass stars Planet












- Slides: 25

Studying cool planets around distant low-mass stars Planet detection by gravitational microlensing Martin Dominik Royal Society University Research Fellow SUPA, University of St Andrews, School of Physics & Astronomy

Deflection of light by gravity (1911) bending angle 2 GM α= c 2ξ measurable at Solar limb: α 0. ″ 85 = suggested: measure during Solar eclipse

Deflection of light by gravity (1915) bending angle 4 GM α= c 2ξ measurable at Solar limb: α 1. ″ 7 = confirmed by measurement of stellar positions during Solar eclipse (Eddington 1919)

Bending of starlight by stars (Gravitational microlensing) You are here S L

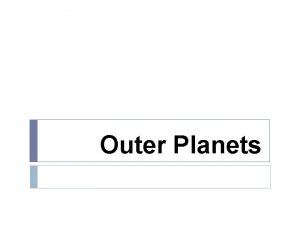
Deriving the gravitational lens equation 4 GM bending angle α = c 2ξ side view DS DL I− L O η S ξ α I+ α

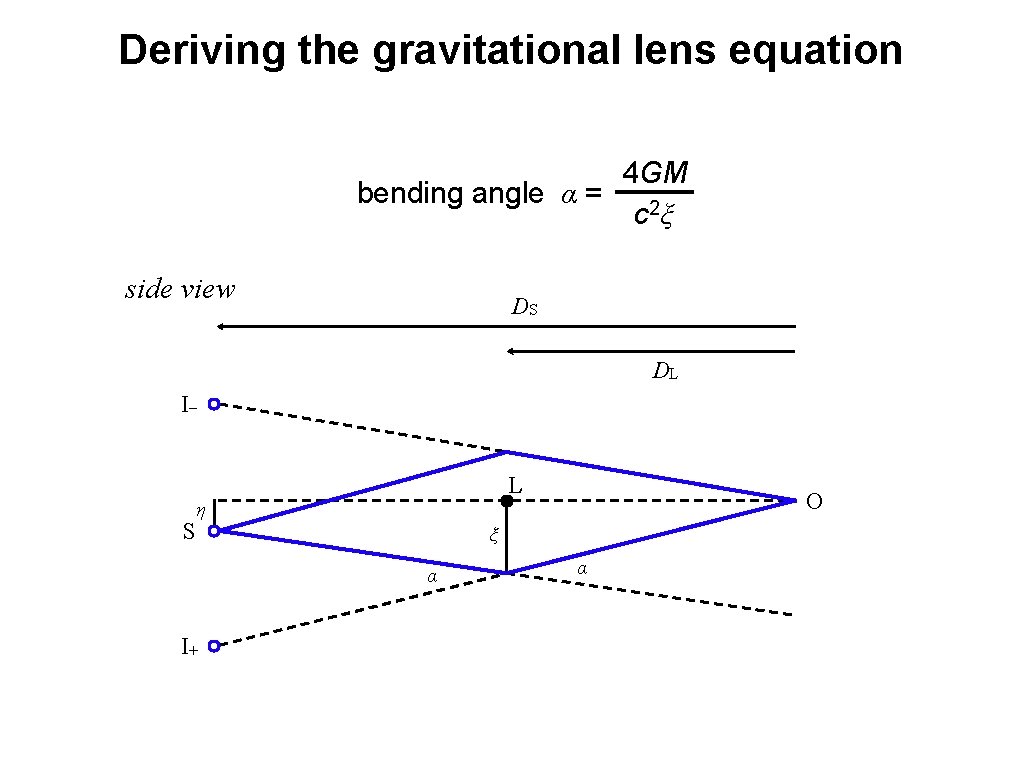
The gravitational lens equation and its solutions side view 4 GM bending angle α = c 2ξ I− η angular Einstein radius 4 GM DS−DL θE = c 2 DL DS ξ I+ ξ x= DL θE η y= DS θE two images y = x − 1 ( ) 1 x (lens equation) x± = 2 [y ± (y 2+4)1/2] 1/2

Image distortion and magnification angular Einstein radius 4 GM DS−DL θE = c 2 DL DS observer’s view ( ) 1/2 with ‘typical’ DS ~ 8. 5 kpc and DL ~ 6. 5 kpc θE ~ 600 (M/M☉ )1/2 μas x± = 1 2 [y ± (y 2+4)1/2] lens equation relates radial coordinates, polar angle conserved dx± radial distortion dy total magnification x± tangential distortion y A(y) = ∑ ± x± dx± y dy = y 2+2 y (y 2+4)1/2

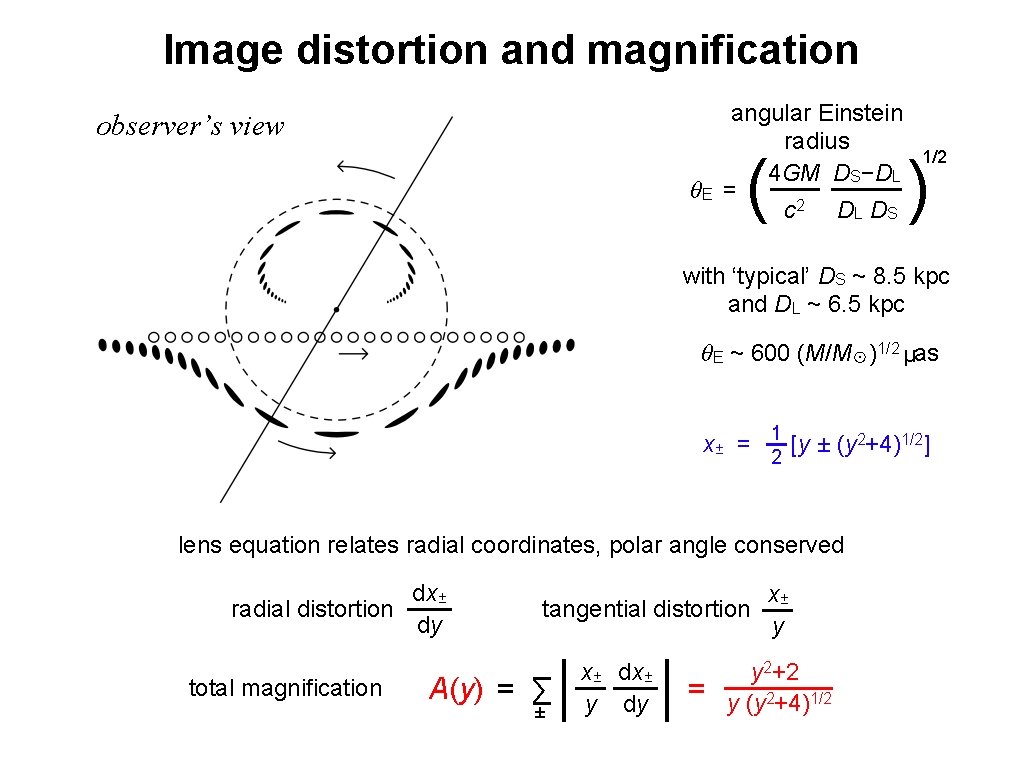
Microlensing light curves S L (t-t 0)/t. E = θE/μ y(t) = [u 02 + ( t − t 0 t. E )2]1/2 A(y) = A[y(t)] defined by u 0, t. E μ ~ 15 μas d-1 t. E ~ 40 (M/M☉ )1/2 days y 2+2 y (y 2+4)1/2

Notes about gravitational lensing dated to 1912 on two pages of Einstein’s scratch notebook


Microlensing optical depth quantify alignment by defining optical depth τ = probability that given source star is inside Einstein circle u < 1 ⇔A > 3/√ 5 ≈ 1. 34 corresponds to brightening in excess of 34% Solid angle of sky covered by NL Einstein circles (neglect overlap) NL πθE 2 with mass volume density ρ(DL) and mass spectrum f(M) N→ ∫ f(M) DL 2 ρ(DL) M ∫f(M) d. M = 1 d. DL dΩ d. M for ρ = const. , x = DL/DS θE = 2 I ( τ = 4πG DS ρ x(1 -x) dx = 2πG ∫ 0 c 2 3 c 2 ρ DS ~ 8 kpc, Galactic disk ρ = 0. 1 35% disk, 65% bulge M☉ (pc)3 4 GM DS−DL c 2 DL DS 1/2 ) DS 2 τ ~ 6 × 10 -7 (Galactic disk) τ ~ 2 × 10 -6 (total)

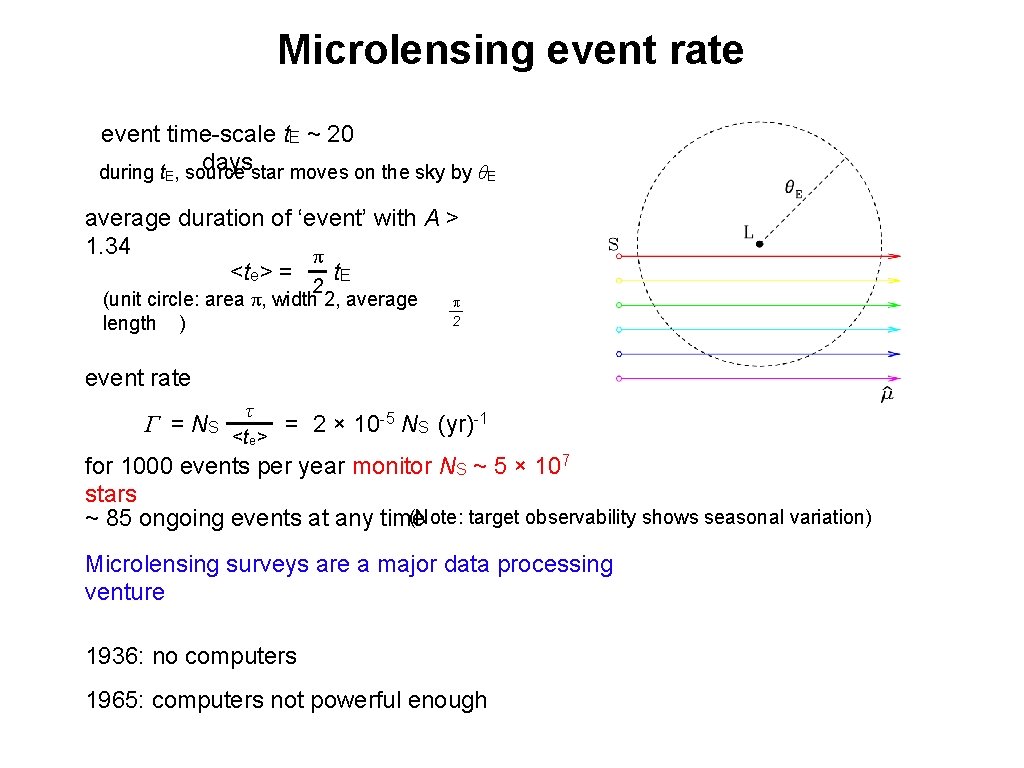
Microlensing event rate event time-scale t. E ~ 20 daysstar moves on the sky by θE during t. E, source average duration of ‘event’ with A > 1. 34 π <te> = t. E 2 (unit circle: area π, width 2, average length ) π 2 event rate Γ = NS τ <te> = 2 × 10 -5 NS (yr)-1 for 1000 events per year monitor NS ~ 5 × 107 stars (Note: target observability shows seasonal variation) ~ 85 ongoing events at any time Microlensing surveys are a major data processing venture 1936: no computers 1965: computers not powerful enough

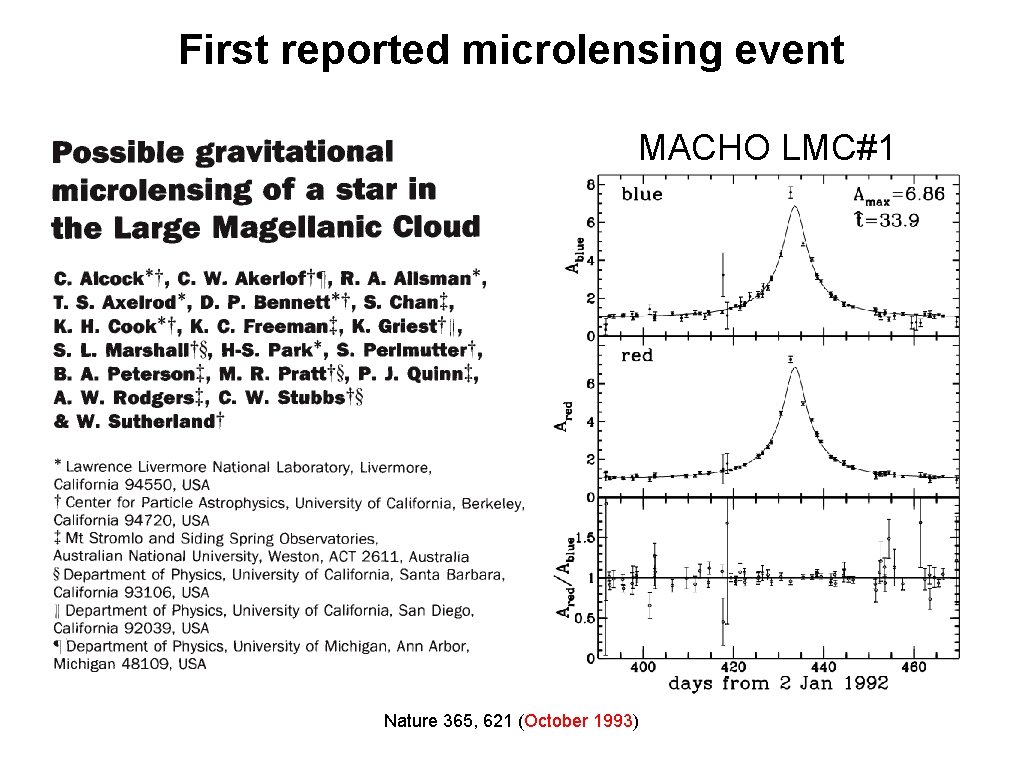
First reported microlensing event MACHO LMC#1 Nature 365, 621 (October 1993)

Current microlensing surveys (2007) Optical Gravitational Lensing Experiment 1. 3 m Warsaw Telescope, Las Campanas (Chile) 1. 8 m MOA Telescope, Mt John (New Zealand) daily monitor ≳ 100 million stars, -6 τ ~ 10 for microlensing event → ~1000 events alerted per year

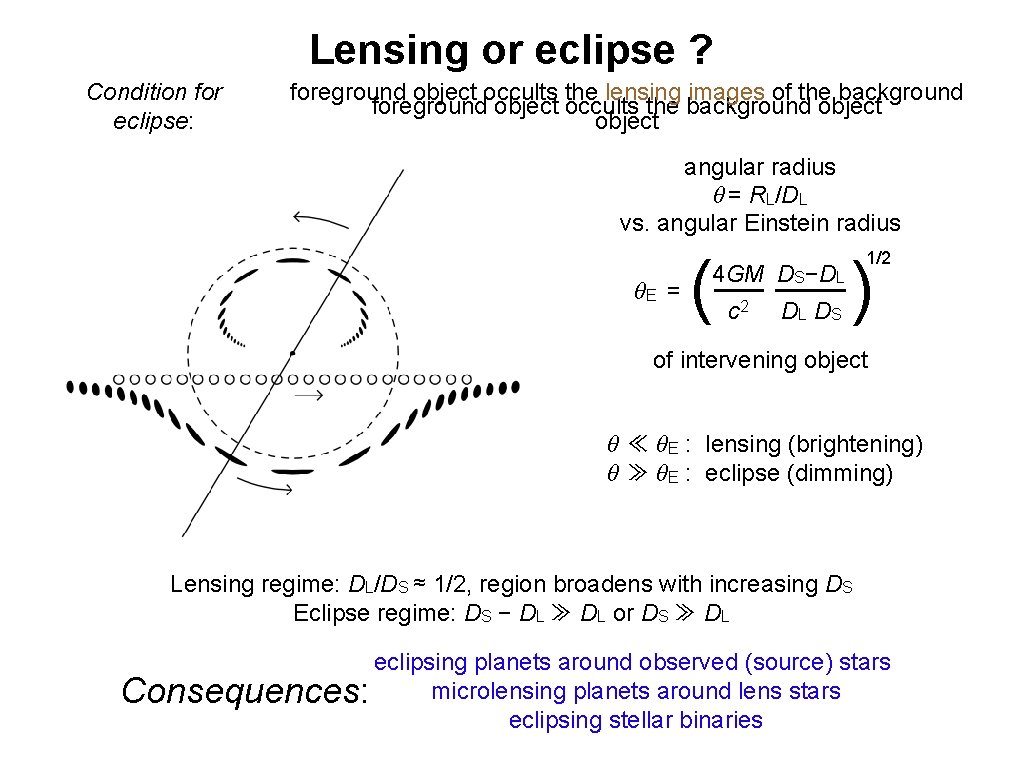
Lensing or eclipse ? Condition for eclipse: foreground object occults the lensing images of the background foreground object occults the background object angular radius θ = RL/DL vs. angular Einstein radius θE = ( 4 GM DS−DL c 2 DL DS ) 1/2 of intervening object θ ≪ θE : lensing (brightening) θ ≫ θE : eclipse (dimming) Lensing regime: DL/DS ≈ 1/2, region broadens with increasing DS Eclipse regime: DS − DL ≫ DL or DS ≫ DL eclipsing planets around observed (source) stars microlensing planets around lens stars Consequences: eclipsing stellar binaries

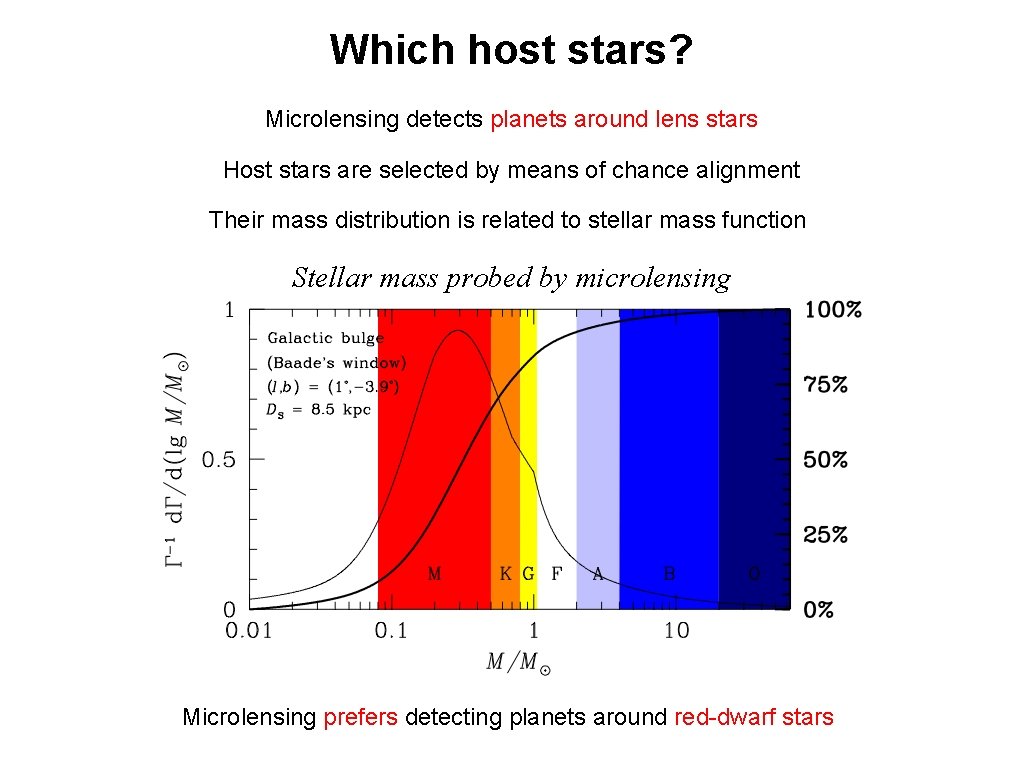
Which host stars? Microlensing detects planets around lens stars Host stars are selected by means of chance alignment Their mass distribution is related to stellar mass function Stellar mass probed by microlensing Microlensing prefers detecting planets around red-dwarf stars

Multiple point-mass lens x y = x − |x|2 lens equation (2 D) for single point-mass lens θ x= θE two-dimensional position angles β (source) and θ (image) angular Einstein radius total mass M, θE = ( 4 GM DS−DL c 2 DL DS i-th object with mass fraction mi at x(i), β y= θE ) 1/2 ∑ mi = 1 in weak-field limit, superposition of deflection terms, but not of light curves x − x(i) y = x − ∑ mi |x − x(i)|2

The binary point-mass lens angular separation δ = d θE mass ratio q = m 2/m 1 m 2 = 1 − m 1 completely characterized by two dimensionless parameters (d, q) time-scale of planetary deviations ≪ orbital period m 1 = in centre-of-mass system: y 1 = x 1 − 1 1+q y 2 = x 2 − 1 1+q x(1) q 1+q x 1 − ( x 1 − 1 1+q q 1+q = m 2 = ( d 2 d ) + x 2 2 x 2 ( x 1 − q 1+q 2 d ) + x 22 q 1+q d, 0) − q 1+q x(2) = −( 1 1+q x 1 + ( x 1 + 1 1+q d, 0) d 2 d ) + x 22 x 2 ( x 1 + 1 1+q 2 d ) + x 22 solving for (x 1, x 2) leads to 5 th-order complex polynomial either 3 or 5 images

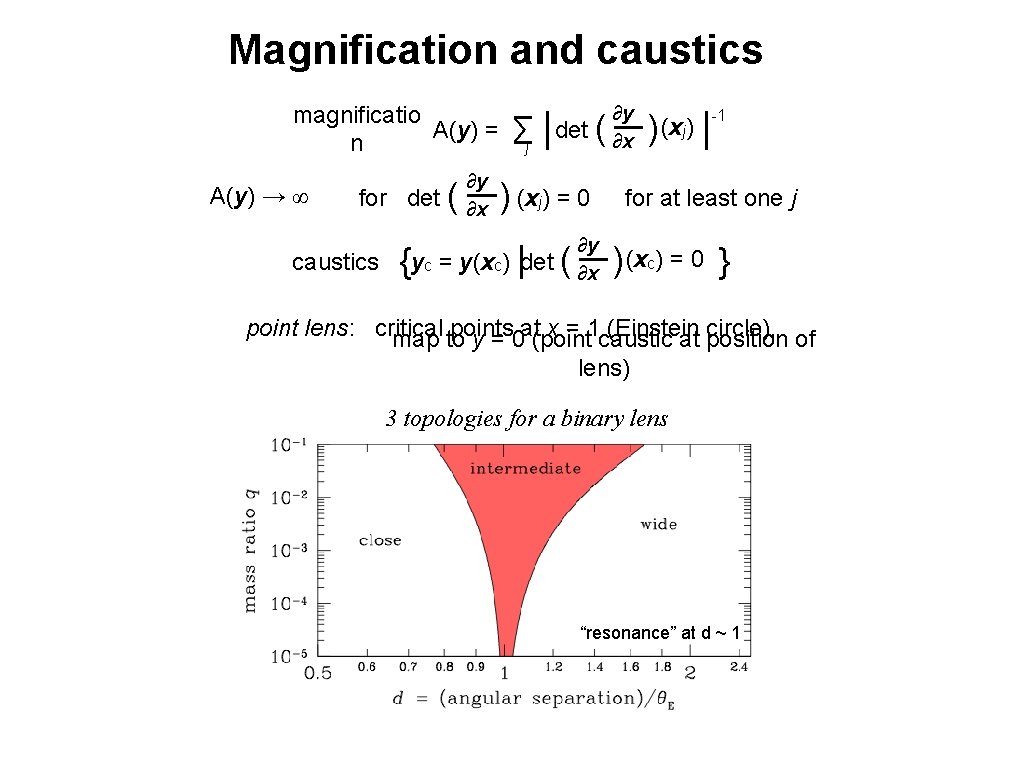
Magnification and caustics magnificatio A(y) = n A(y) → ∞ for det ( caustics ∂y ∂x ∑j | det ( ) (xj) = 0 {yc = y(xc) |det ( ∂y ∂x ) (xj) | -1 for at least one j ) (xc) = 0 } point lens: critical points x = 1 caustic (Einstein circle), of map to y = 0 at(point at position lens) 3 topologies for a binary lens “resonance” at d ~ 1

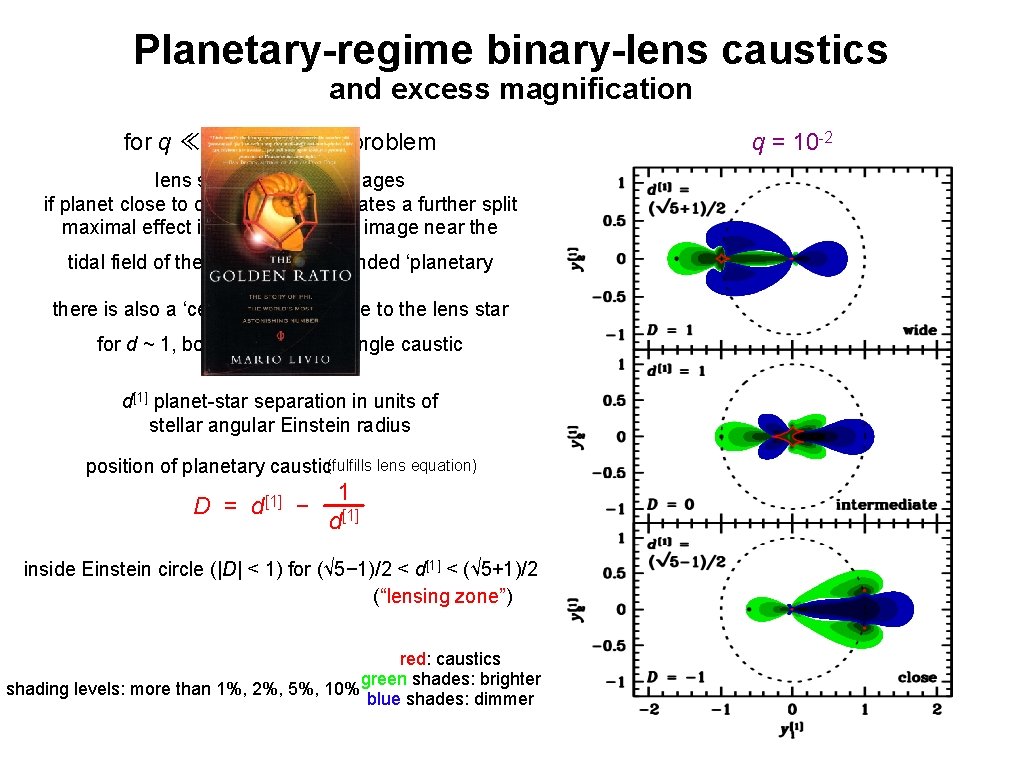
Planetary-regime binary-lens caustics and excess magnification for q ≪ 1: two-scale problem lens star produces 2 images if planet close to one of these, it creates a further split maximal effect if lens star creates image near the planet tidal field of the star creates extended ‘planetary caustic’ there is also a ‘central caustic’ close to the lens star for d ~ 1, both merge into a single caustic d[1] planet-star separation in units of stellar angular Einstein radius position of planetary caustic(fulfills lens equation) D = d[1] 1 − [1] d inside Einstein circle (|D| < 1) for (√ 5− 1)/2 < d[1] < (√ 5+1)/2 (“lensing zone”) red: caustics green shades: brighter shading levels: more than 1%, 2%, 5%, 10% blue shades: dimmer q = 10 -2

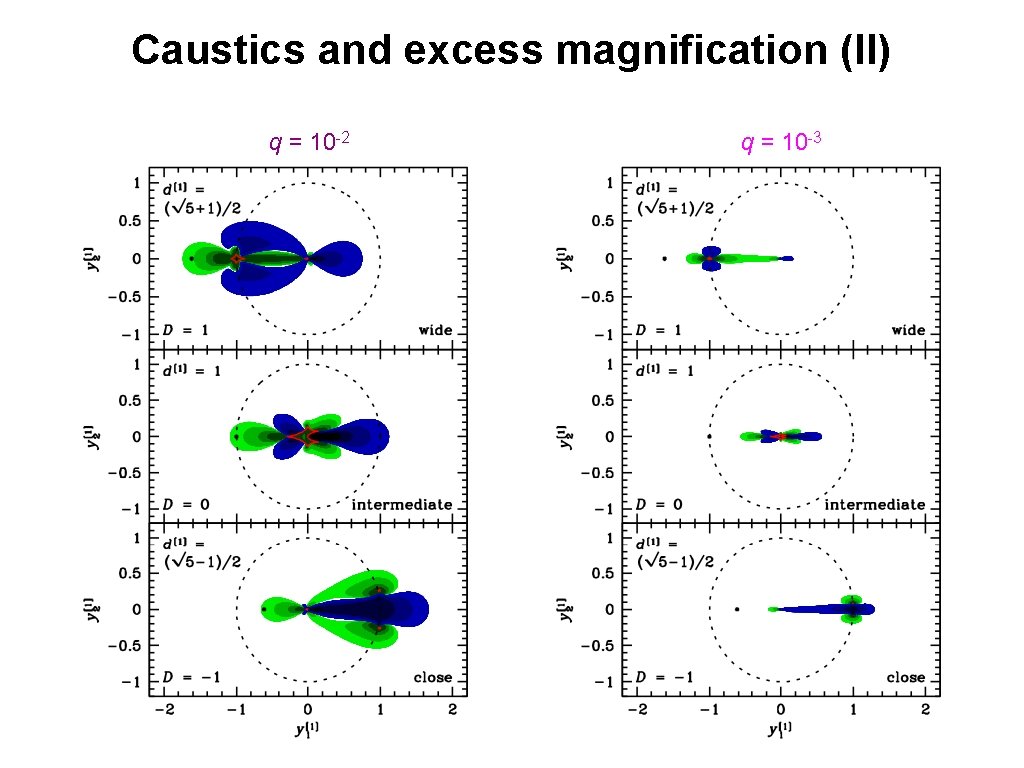
Caustics and excess magnification (II) q = 10 -2 q = 10 -3

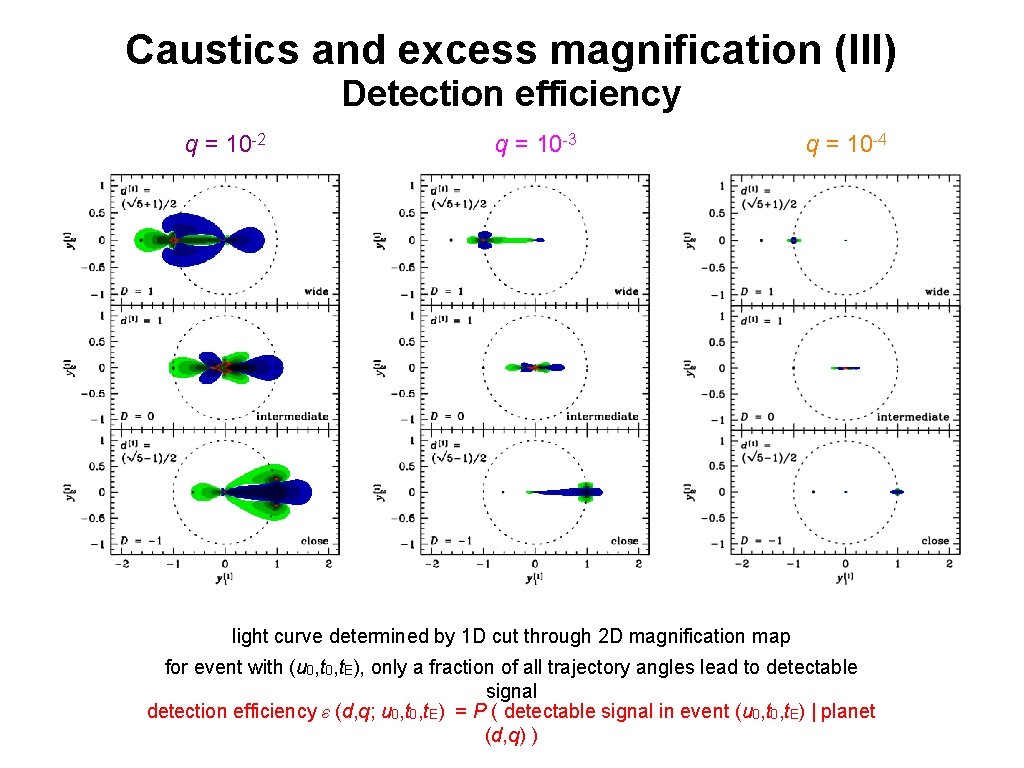
Caustics and excess magnification (III) Detection efficiency q = 10 -2 q = 10 -3 q = 10 -4 light curve determined by 1 D cut through 2 D magnification map for event with (u 0, t. E), only a fraction of all trajectory angles lead to detectable signal detection efficiency ε (d, q; u 0, t. E) = P ( detectable signal in event (u 0, t. E) | planet (d, q) )

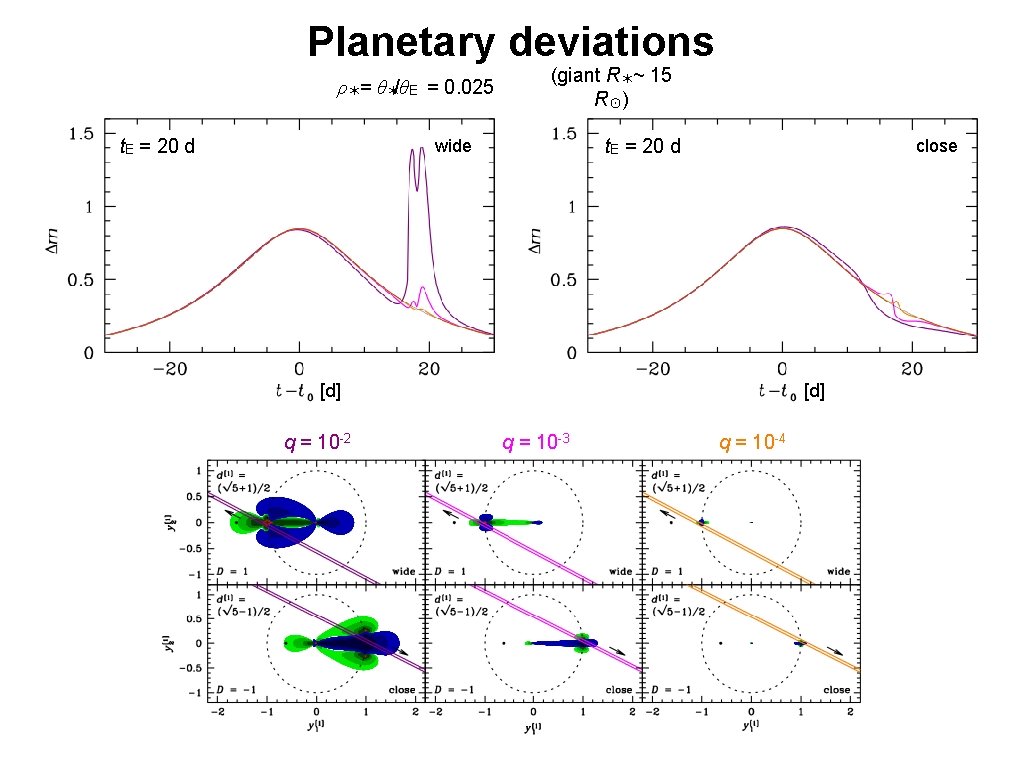
Planetary deviations ρ✶= θ✶/θE = 0. 025 t. E = 20 d (giant R✶~ 15 R☉ ) t. E = 20 d wide close [d] q = 10 -2 [d] q = 10 -3 q = 10 -4

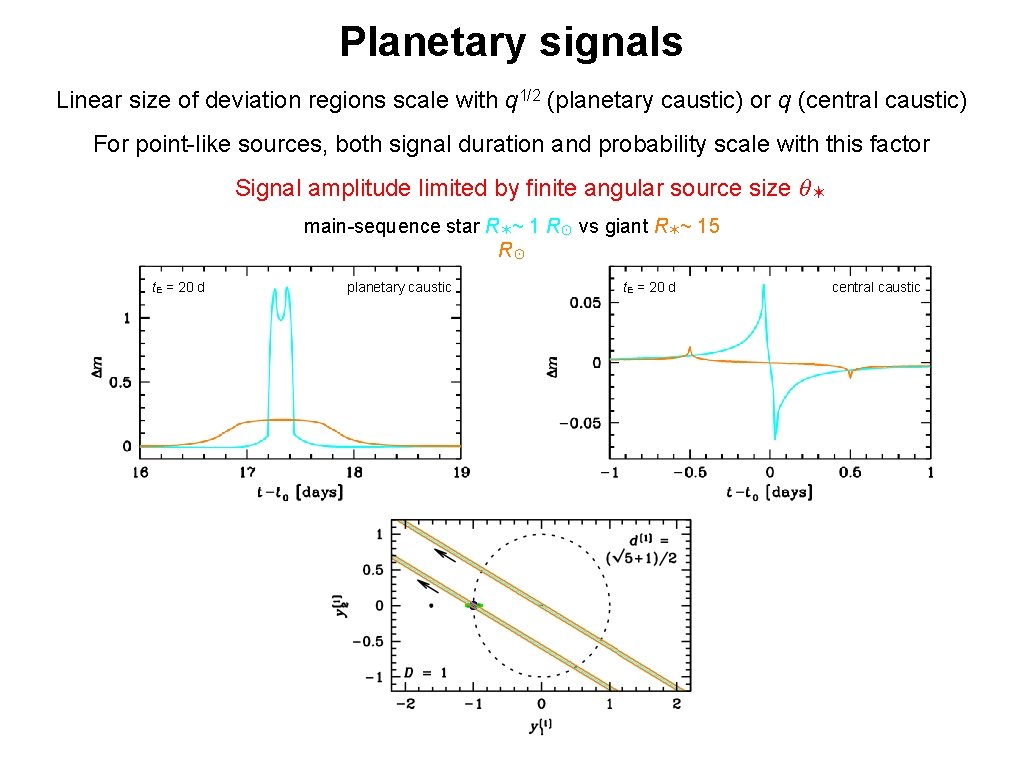
Planetary signals Linear size of deviation regions scale with q 1/2 (planetary caustic) or q (central caustic) For point-like sources, both signal duration and probability scale with this factor Signal amplitude limited by finite angular source size θ✶ main-sequence star R✶~ 1 R☉ vs giant R✶~ 15 R☉ t. E = 20 d planetary caustic t. E = 20 d central caustic

 What is each planet made of
What is each planet made of Inner planets and outer planets
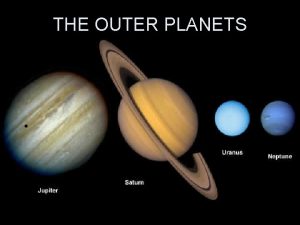
Inner planets and outer planets The four outer planets
The four outer planets Why do jovian planets have rings
Why do jovian planets have rings What separates inner and outer planets
What separates inner and outer planets Studying our living planet
Studying our living planet The stars there are millions of stars in the sky
The stars there are millions of stars in the sky Why earth is called blue planet
Why earth is called blue planet Examples of what goes around comes around
Examples of what goes around comes around Martin luther king of hinduism
Martin luther king of hinduism Distant
Distant Aims are
Aims are Cannibal inhabitants of a distant land
Cannibal inhabitants of a distant land Lod example
Lod example Retrograde motion of mars
Retrograde motion of mars Peace is not merely a distant goal
Peace is not merely a distant goal Dips his wings in the orange sun rays meaning
Dips his wings in the orange sun rays meaning Always-on
Always-on Distant past tense
Distant past tense Non western artists
Non western artists Distant
Distant Researchers who are studying a new shampoo
Researchers who are studying a new shampoo Lesson 1 studying geography
Lesson 1 studying geography Lesson 128
Lesson 128 Culture or way of living station 1
Culture or way of living station 1 Studying in sweden as an eu citizen
Studying in sweden as an eu citizen