Stime per intervalli Oltre al valore puntuale di

Stime per intervalli Oltre al valore puntuale di una stima, è interessante conoscere qual è il margine di errore connesso alla stima stessa. Si possono stabilire dei limiti entro i quali si ha una probabilità (1 - ) che vi sia compreso il vero valore del parametro nella popolazione. (e conseguentemente sia la probabilità che nell’intervallo non sia compreso il vero valore del parametro) Questi limiti si chiamano LIMITI FIDUCIALI, e l’intervallo che definiscono si chiama INTERVALLO FIDUCIALE. Una stima di n parametro di un campione, corredata dai suoi limiti fiduciali, è detta STIMA PER INTERVALLI. I valori usuali di sono 0, 01; 0, 05; 0, 1, che danno luogo a intervalli fiduciali rispettivamente del 99; 95; 90% (di probabilità che entro essi sia compreso il vero valore del parametro)

Deviazione standard nota Il caso più semplice è quando si conosce la deviazione standard di una popolazione, ma non la media. In tal caso si estrae un campione per stimare la media. La media del campione è un appartenente alla popolazione di medie campionarie che ha la stessa media della popolazione di partenza e deviazione standard = a n. Se vengono individuate le due ordinate che, nella curva normale di media = media del campione e = n, che escludono, da ambo i lati /2, l’intervallo tra le 2 ordinate avrà probabilità di includere la vera media della popolazione. i limiti fiduciali si restringono all’aumentare di: • (si esclude un’area di curva maggiore e quindi le 2 ordinate sono più vicine), ma aumenta la probabilità che non contengano • n (e non vi sono controindicazioni, se non il costo o l’onere di un campione più grande)

Deviazione standard nota (segue) Si tratta quindi di risolvere la seguente equazione, in cui le incognite compaiono agli estremi di integrazione: Per simmetria, si può considerare uno solo dei 2 integrali: Questa equazione è di difficile soluzione, ma se = 1 e =0 è risolvibile in z, poiché l’integrale è tabulato e basta ritrovare il valore di /2 nel corpo della tabella per risalire a z. dato che z = (m- )/ , è possibile risalire al valore dell’estremo di integrazione che soddisfa l'uguaglianza: Limsup = m + z ; per simmetria il limite inferiore sarà m - z. Quindi, con probabilità di sbagliare: m - z

Deviazione standard ignota E’ il caso più frequente in realtà: tipicamente si campiona da popolazioni delle quali non si conosce alcun parametro, e si assume che siano distribuite normalmente. In questo caso dal campione si deve stimare la media e la deviazione standard. Ne consegue che gli intervalli fiduciali saranno più “larghi” di quelli con d. s nota, poiché vi sono due stime (m e s) soggette a fluttuazioni campionarie. Non si può usare la distribuzione di z, poiché per usare z occorre conoscere , che in questo caso è invece stimato. E’ però nota la distribuzione di: Che è nota come distribuzione del t di Student. Non ve ne è una sola, ma infinite, in funzione della dimensione campionaria. Per n= la distribuzione del t diviene quella di z.

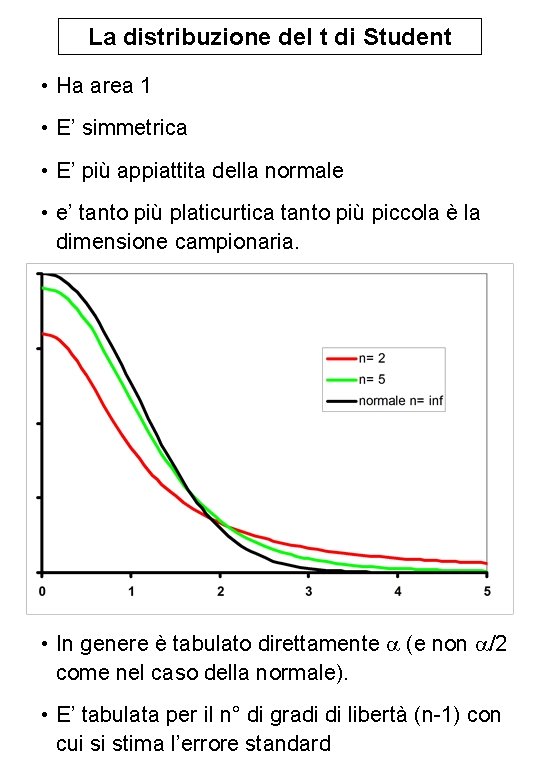
La distribuzione del t di Student • Ha area 1 • E’ simmetrica • E’ più appiattita della normale • e’ tanto più platicurtica tanto più piccola è la dimensione campionaria. • In genere è tabulato direttamente (e non /2 come nel caso della normale). • E’ tabulata per il n° di gradi di libertà (n-1) con cui si stima l’errore standard