Secure Hashed DiffieHellman over NonDDH Groups Rosario Gennaro

Secure Hashed Diffie-Hellman over Non-DDH Groups Rosario Gennaro (IBM) Hugo Krawczyk (Technion, IBM) Tal Rabin (IBM) 1

Diffie-Hellman n Cyclic group G, generator g, (ga, gb) -> gab n Main applications: key exchange, encryption n DDH: gab random element in G (even given ga, gb) ¨ (ga, gb, gab) n (ga, gb, gc), a, b, c R [ord(G)] Are random group elements what we are interested in as output from DH? ¨ Not really. What is usually needed: A random key K in {0, 1}k (e. g. k=128) ¨ True in the case of KE as well as encryption (eg [BJN 00]) 2

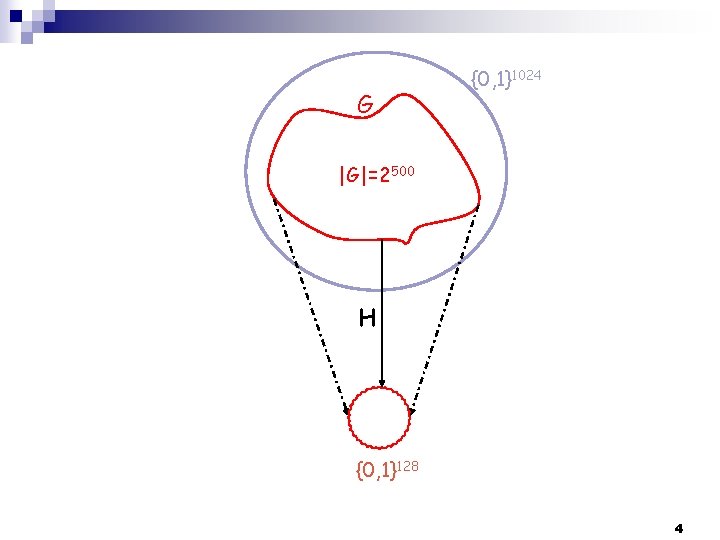
From random group elements to random keys (strings ( n The solution: hash gab into a k-bit string n DDH hashing gab is computationally equivalent to hashing a random element from G n n Question: Which hash functions can convert the uniform distribution on G into the uniform dist’n on {0, 1}k? Answer [leftover hash lemma]: “ 2 wise-independent” hash functions will map G almost uniformly over {0, 1}k è if G is DDH then K=H(gab) is pseudorandom Note: length of K log|G|-160 3

G {0, 1}1024 |G|=2500 H {0, 1}128 4

Relaxing DDH n n Question: given that we need to hash gab anyway to achieve a pseudo-random output, do we still need to work over a DDH group G? Note that the DDH requirement is not for free: e. g. , it disqualifies working over Zp* !! ¨ DDH does not hold on any group with small divisors n For example: in Zp* can distinguish QRs from non-QRs n DDH believed to hold in large prime order groups But, is it really insecure to do (hashed) DH over non. DDH groups, e. g. over. Zp* ? 5

Our Answer Q: Is it really insecure to do (hashed) DH over non-DDH groups, e. g. over. Zp* ? A: Once you hash you can do secure DH over many non-DDH groups, including. Zp* P L A N: § Relax the notion of DDH: t-DDH § Show that hashed DH is secure over t-DDH groups (for large enough t) § Show there are interesting examples of t-DDH groups § In particular: hashed DH over Zp* (for random p) is secure 6

Relaxing DDH n n Since we are hashing gab then we do not need gab to be totally random in G but contain enough randomness that a good hash function can extract More precisely, we need to extract from gab “all its computational entropy” ¨ n statistical entropy is 0 since gab is fully determined by ga and gb “Def’n”: G is t-DDH if for a, b R {1. . |G|} the DH value gab has “t bits of computational entropy” even when ga and gb are given More formally… 7

min-entropy n A probability distribution X over a set S has min-entropy t if for all s S, Prob. X(s) 2 -t ¨ Not all elements necessarily equi-probable, but no single element is too “heavy” Uniform Distribution Min-entropy t Computational min-entropy t computationally indisting’ble from a distribution with min-ent t 8

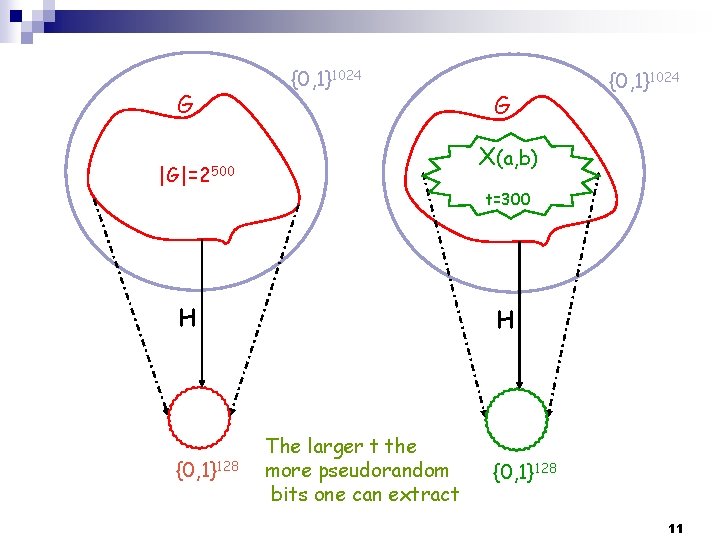
t-DDH: A Relaxation of DDH n G satisfies the t-DDH assumption if for each pair a, b there exists a distribution X(a, b) over {1. . |G|} such that 1. X(a, b) has min-entropy t 2. (ga, gb, gab) (ga, gb, gc), a, b R {1. . |G|}, c R X(a, b) (i. e. , gab has t bits of “computational entropy” even after seeing ga, gb) Note: existence vs. samplability 9

t-DDH: A Useful Relaxation n n Why? Because if G is t-DDH then hashing gab to <t bits provides a pseudorandom output, namely: Leftover Hash Lemma + t-DDH ¨ Let G be t-DDH and H be a pairwise independent hash family with range {0, 1}t-2 e ¨ Then the distributions (h, ga, gb, h(gab)) and (h, ga, gb, r) for a, b R {1. . |G|}, h RH and r R{0, 1}t-2 e are 2 -e-indistinguishable n The larger t the more pseudorandom bits one can extract 10

G {0, 1}1024 X(a, b) |G|=2500 t=300 H H {0, 1}128 G {0, 1}1024 The larger t the more pseudorandom bits one can extract {0, 1}128 11

Examples of t-DDH groups n G DDH For all a, b: X(a, b) = {1. . |G|} with uniform distribution (here t=log |G|) ¨ i. e. , G is DDH iff G is t-DDH with t=log |G| n Zp*, p=2 q+1. If a or b are even then X(a, b)={2, 4, …, 2 q} (uniform dist’n); if both a and b odd then X(a, b)={1, 3, …, 2 q-1} (uniform dist’n) ¨ i. e. , in this case: Zp* is |q|-DDH (X(a, b) has min-ent |q|) 12

t-DDH: A Useful Relaxation? n Are there “interesting examples” of t-DDH groups, i. e. non-DDH groups that are t-DDH for large t? ¨ Beyond n the “toy case” Z*2 q+1 Yes. Essentially any group with a large DDH SUB -group has guaranteed large min-entropy! 13

The Max-Subgroup Theorem n For all G, G is |m|-DDH where m is the order of the maximal* DDH subgroup in G è can get the WHOLE entropy of a DDH subgroup without having to work over it (or even know it!) *More precisely… theorem holds for the disjoint DDH subgroup maximal ¨ H G is a “disjoint subgroup” if (|H|, |G|/|H|)=1 (e. g. , |G|=2 32 52, then G 18 is disjoint but G 90 is not) ¨ The theorem as written above holds if all the large prime-power subgroups of G are DDH (or if |G| is square-free) 14

Combining Entropy n By the Max-Subgroup Theorem: ¨ we can get the WHOLE entropy of a DDH subgroup without having to work over it n Moreover: we can get the COMBINED entropy of ALL large prime-power subgroups ¨ E. g. p-1=s·q 1·q 2, |q 1|=|q 2|=160 (q 1, q 2 not divide s) then Zp* is 320 -DDH 15

Direct Product Characterization n A cyclic group G is DDH if and only if its prime-power subgroups are DDH all ¨ If G is DDH then all its subgroups are DDH (thus, DDH on large prime-order groups is a “minimal assumption”) ¨ If G 1, G 2 are DDH groups of disjoint order then G 1 x. G 2 is DDH. i. e. (|G 1|, |G 2|)=1 Example: if p-1=s·q 1·q 2, |q 1|=|q 2|=160, and s is not divisible by q 1 and q 2 then Zp* is 320 -DDH (max subgroup + DPC theorems) 16

Application to Zp* for random p n n Traditionally, working over Zp* requires knowledge of the factors of p-1 ¨ either for choosing a generator of Zp* (full factorization) ¨ or for choosing a generator of large order q for q/p-1 Our results allow to use Zp* for random p w/o any knowledge of the factors of p-1 * ¨n. Choose use as a generator. That’s it! R Zp and Honestg users need notg know anything about the n It is guaranteed, with v. h. p. , that the subgroup G=<g> contains all factorization of p-1 large-prime order subgroups of Zp* On the other hand, thesubgroups function secure Assuming large-prime order of remains Zp* are DDH G is t-DDH for sufficiently large t eventhen if the attacker knows this factorization! n n (Max-Subgroup + Direct Product Characterization Theorems) 17

DH with short exponents n n A disadvantage of working over Zp* is that exponents are |p|-bit long. In contrast, working over Gq takes only |q|-bit exponents (e. g. , |q|=300 vs |p|=1024) Yet, a common practice (e. g. , IPsec) is to work over Zp* using exponents of length 200 (significant speed-up) Can we apply our results to the latter case? Yes, if t-DDH holds in a group G then it also holds for exponents of length s provided the discrete log problem with exponents of size s is hard in G 18

Summary n Hashed DH over non-DDH groups, ¨ Defined a DDH relaxation, t-DDH, and showed its sufficiency for hashed DH ¨ Showed how t is determined by the max DDH subgroup. Thus, hashed-DDH can use all the entropy in the DDH subgroups w/o having to know (or work over) these subgroups ¨ Proved the DDH Direct Product Characterization: G is DDH if and only if all its prime-power subgroups are DDH ¨ Illustrated applications via Zp* (w/ or w/o known factorz’n) ¨ Results preserved under short exponents ¨ Results are generic (any cyclic group) 19