Rules of Logarithms Growth and Decay MICHAEL DEL


























- Slides: 35

Rules of Logarithms & Growth and Decay MICHAEL DEL VECCHIO

Review – Definition of Logarithm Suppose b > 0 and b ≠ 1, then there exists a number “p” such that: Logb n = p ↔ bp = n For Example: Let b = 2 and p = 32 Logb n = p ↔ bp = n Log 2 32 = 5 ↔ 25 = 32

Review – Convert Between Forms Exponential to Logarithmic 23 = 8 Log 2 8 = 3 42 = 16 Log 4 16 = 2 Logarithmic to Exponential Log 3 81 = 4 34 = 81 Log 2 1/8 = -3 2 -3 = 1/8

Keep In Mind Log 3 9 b = 3 n = 9

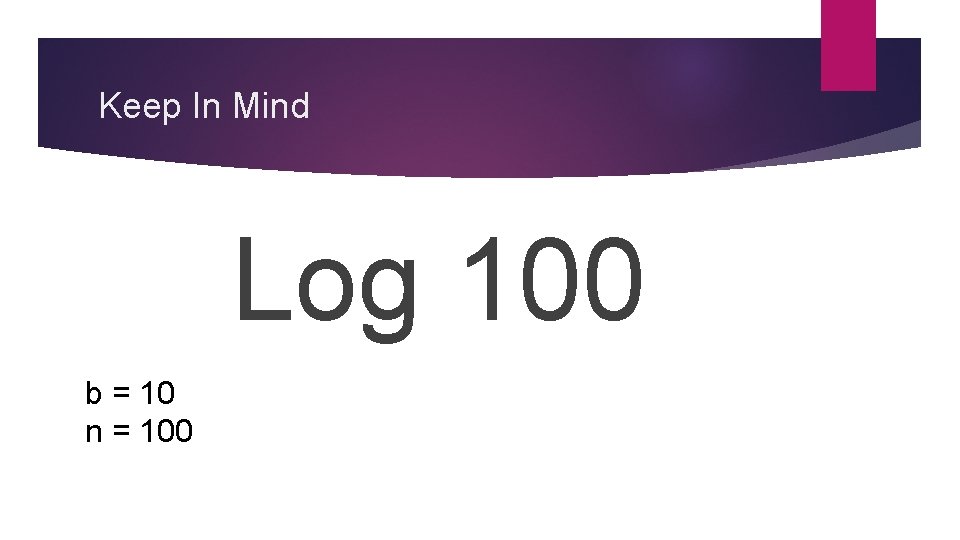
Keep In Mind Log 100 b = 10 n = 100

Keep In Mind Log 100 ≡ Log 10 100

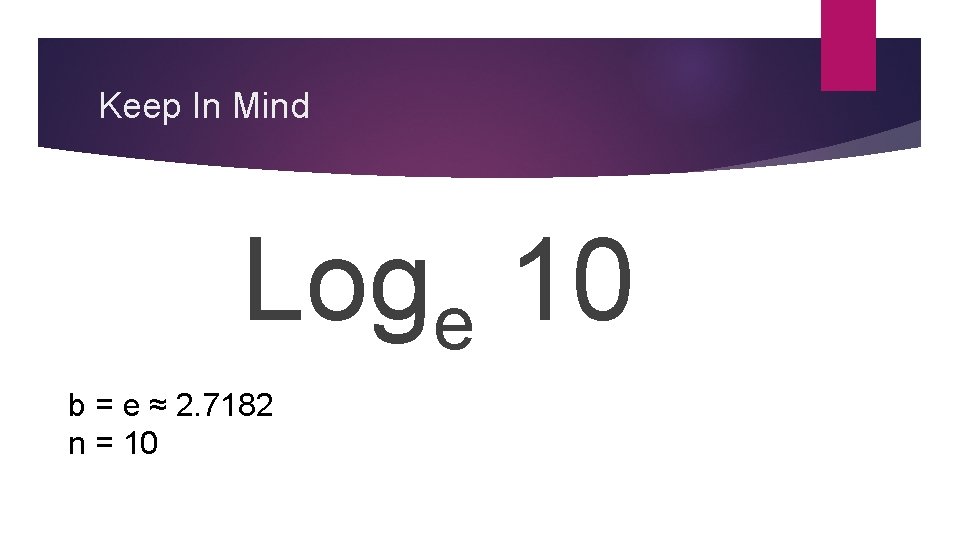
Keep In Mind Loge 10 b = e ≈ 2. 7182 n = 10

Keep In Mind Loge 10 ≡ Lne 100 ≡ Ln 100

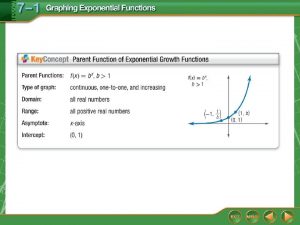
Review – Basic Properties of Logarithms Rule Example For a > 0, a ≠ 1 Loga a = 1 Log 3 3 = 1 Loga 1 = 0 Log 2 1 = 0 Loga ax = x, x real Log 5 52 = 2 aloga x = x, x > 0 2 log 2 5 = 5

Logarithms = Exponents The Answer To A Logarithm Is An Exponent

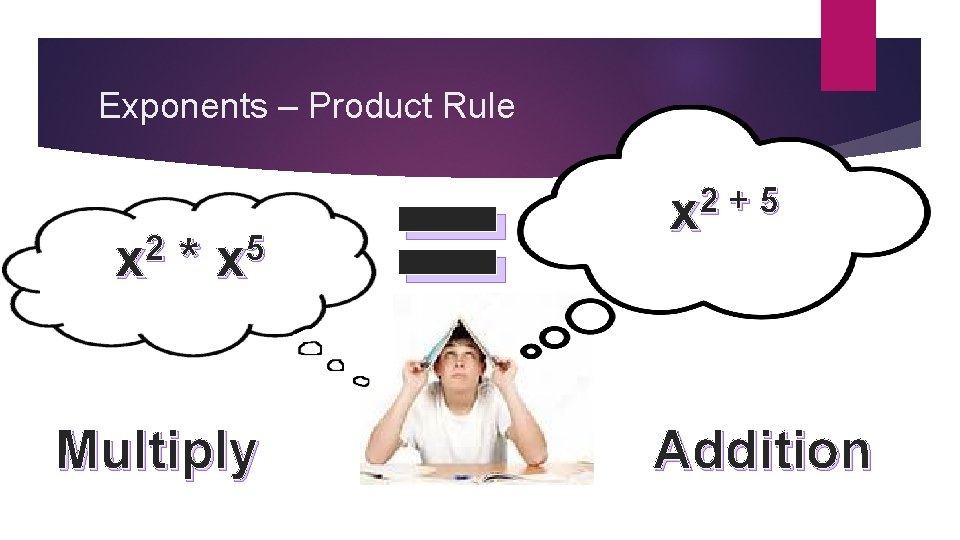
Exponents – Product Rule 2 x * 5 x Multiply = 2 + 5 x Addition

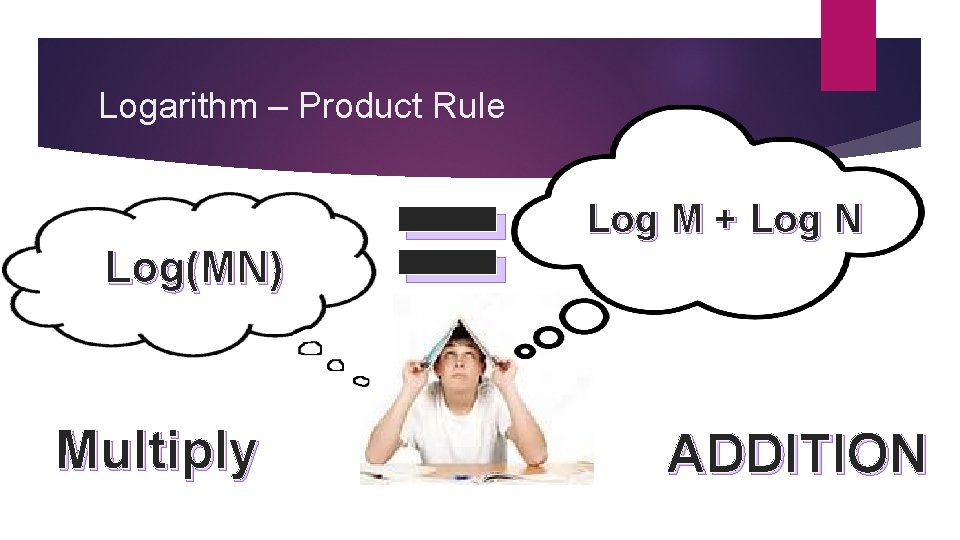
Logarithm – Product Rule Log(MN) Multiply = Log M + Log N ADDITION

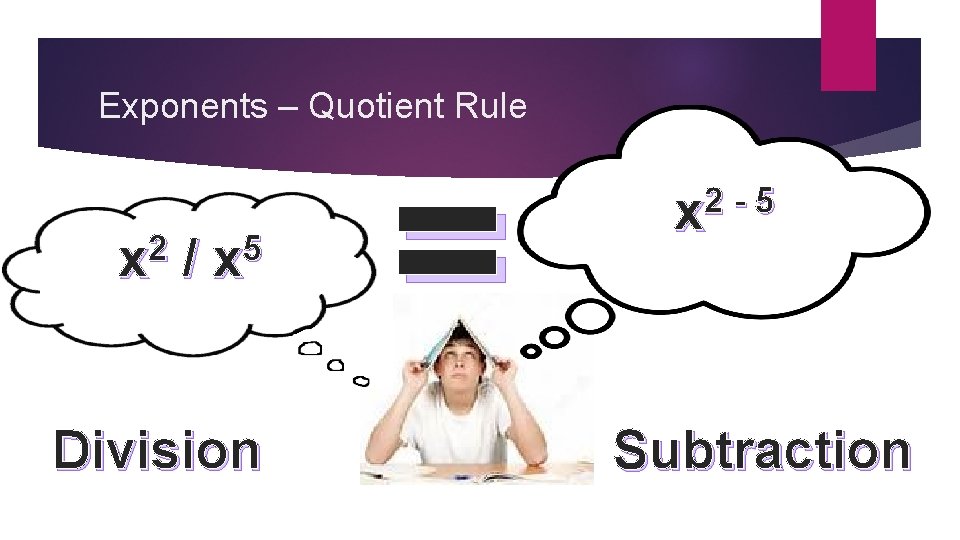
Exponents – Quotient Rule 2 x / 5 x Division = 2 5 x Subtraction

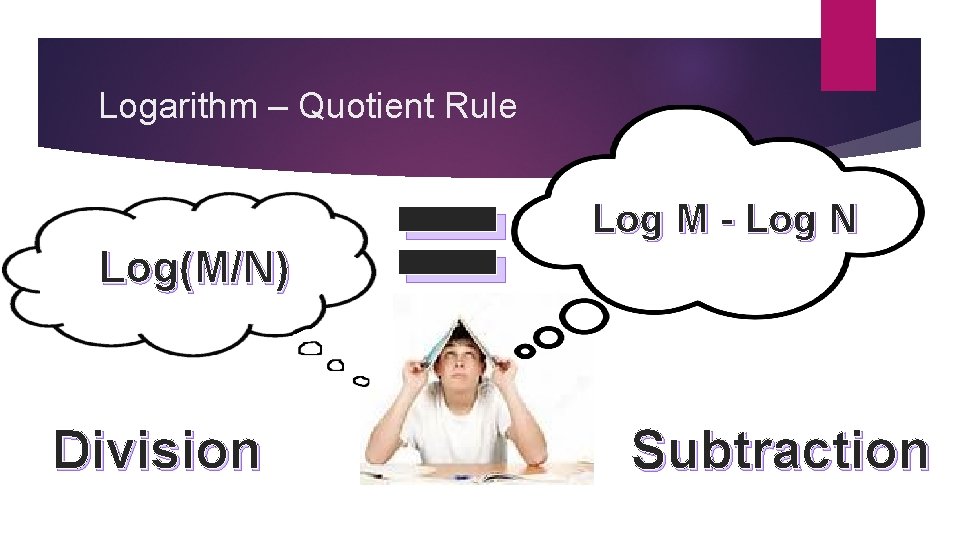
Logarithm – Quotient Rule Log(M/N) Division = Log M - Log N Subtraction

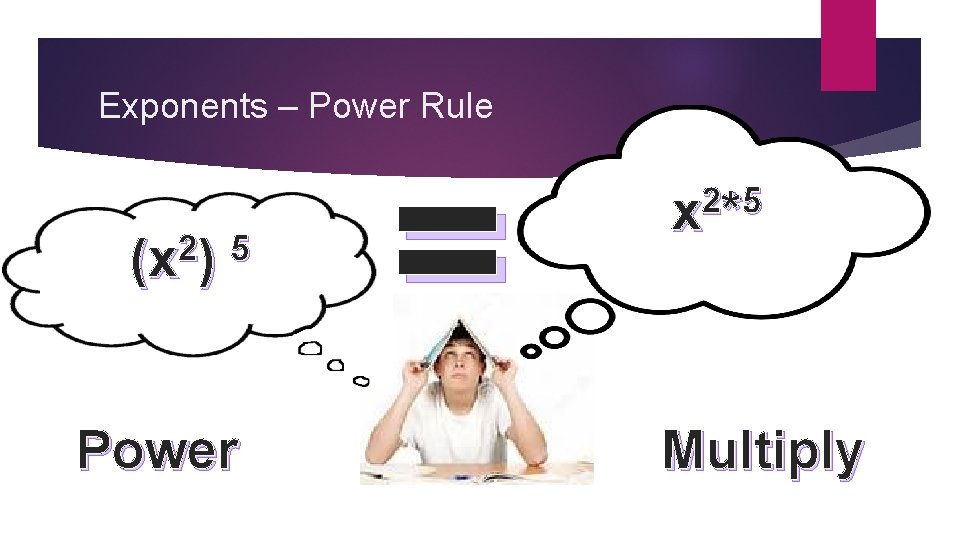
Exponents – Power Rule 2 5 (x ) Power = 2 5 x* Multiply

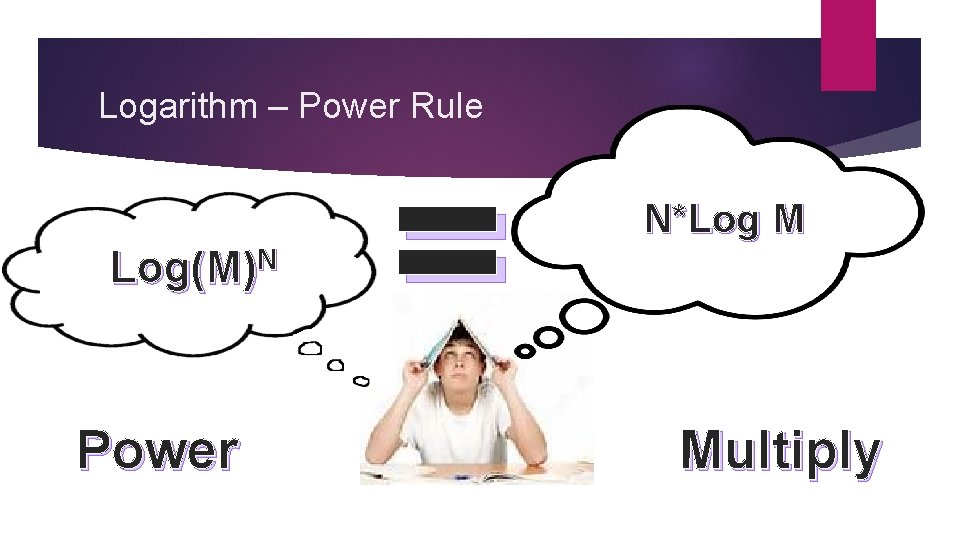
Logarithm – Power Rule Log(M)N Power = N*Log M Multiply

Rules of Logarithms 1. Product Rule Log 2(5*17) = Log 2 5 + Log 2 17 Loga(MN) = Loga M + Loga N 2. Quotient Rule Log(3 x) = Log 3 + Log x Power Rule Loga Mr = r Loga M Quotient Rule Example Ln(5/7) =Ln 5 - Ln 7 Loga(M/N) = Loga M - Loga N 3. Product Rule Example Log(5/x) = Log 5 - Log x Power Rule Example Log 53/2 = 3/2 Log 5 Log 2 7 -3 = -3 Log 2 7

Evaluating Expressions Example: Practice: Let Log 5 z = 3 and Log 5 y = 2 Log 5(y 2 z 3) = Log 5 y 2 + Log 5 z 3 2 Log 5 y + 3 Log 5 z 2(2) + 3(3) 4 + 9 = 13

Writing Expressions in Expanded Form Example: Practice: Log 2 (x 2(x-1)3 )– Log 2 (2 x-1)4 Log (4 xy/z)1/2 Log 2 x 2 + Log 2 (x-1)3 – Log 2 (2 x-1)4 2 Log 2 x + 3 Log 2 (x-1) – 4 Log 2 (2 x-1) ½ Log (4 xy/z) ½(Log (4 xy) – Log z) ½(Log 4 + Log x + Log y – Log z) Log 41/2 + ½ Log x + ½ Log y – ½ Log z) Log 2 + ½ Log x + ½ Log y – ½ Log z)

Writing Expressions in Condensed Form Example: Practice: 2 Ln x + ½ Ln (x 2 + 1) ½ [Log (x + 1) + Log (x – 1)] Ln x 2 + Ln (x 2 + 1) ½ ½ Log[(x+1)(x-1)] Ln (x 2 + 1) ½) ½ Log(x 2 – 1) Ln Log(x 2 – 1) ½ Log

Compute Log 3 15 = ? Calculators Only Do Base 10 and Base e! So How Can We Computer Base 3?

Change of Base Problem: We have: Logb x But we want to have base a: Loga x So we want to go from base a to base b

Change of Base Solution: Let u = Logb x In Exponential Form: x = bu Take Loga of Both Sides: Loga x = Loga bu Solve for u: Loga x = u Loga b u = Substitute Logb x =

Change of Base Formulas (Base a) (Base 10) (Base e)

Compute Log (Base 5) Log 3 15 = Log 5 15 Log 5 3 ≈ 2. 46497

Compute Log (Base 10) Log 3 15 = Log 15 Log 3 ≈ 2. 46497

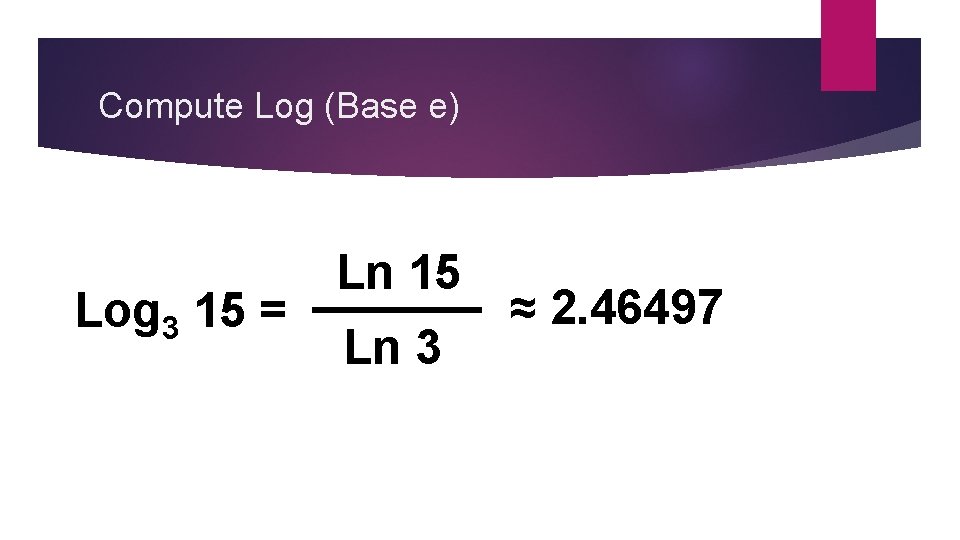
Compute Log (Base e) Log 3 15 = Ln 15 Ln 3 ≈ 2. 46497

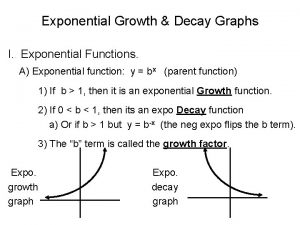
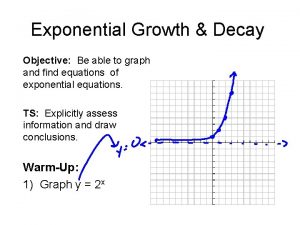
Growth and Decay Formula Say we have some Amount at time t = 0 Exponetial Form: A(t = 0) = A 0 Logarithmic Form: Ln ( A 0 / A(t)) = kt Then after time t we measure quantity A(t) = A 0 ekt Growth Occurs: A(t = t) = A(t) k > 0 Decay Occurs: k < 0

Half-Life and Half-Life Formula The Half-Life of any quantity whose value decreses with time is the time required for the quantity to decay to half of its original value. Amount A 0 decays to ½ Ao in time h A 0 A(t) = ½ A 0 t = h Logarithmic Form: Ln ( A 0 / A(t)) = kt Ln ( A 0 / ½ A 0 = kh Ln(1/2) = kh Ln 1 – Ln 2 = kh Half-Life, h = – Ln 2 /k

Half-Life Example 1 (Example 7 in book) In an experiment 18 grams of the radio active element sodium -24 decayed to 6 grams in 24 hours. Find its half-life to the nearest hour. What we know: t = 24 hours A(0) = 18 grams A(t) = A(24) = 6 We can use our Logarithmic Form: Ln( A(t) / A 0 ) = kt Ln(6 / 18) = 24 k

Half-Life Example 1 Step 1: Solve for k Step 2: Use Half-Life Formula Ln(6 / 18) = 24 k h = - Ln 2 / k Ln(1 / 3) = 24 k h = - Ln 2 / (-Ln 3 / 24) h = - 24 Ln 2 / -Ln 3 Ln 1 - Ln 3 = 24 k 24 k = -Ln 3 Using a Calculator: k = -Ln 3 / 24 h ≈ 15 Hours

Half-Life Example 2 (Example 8 In Book) In 1960, a group of specialists from the British Museum in London investigated whether a piece of art containing organic material found in Tutankhamun’s tomb had been made during his reign or whether it belonged to an earlier period. We know King Tut died in 1346 BC and Ruled Egypt for 10 years. What percent of the amount of carbon-14 originally contained in the object should be present in 1960 if the object was made during Tutankamun’s reign? Note: The Half-Life of Carbon-14 is known to be 5700 Years

Half-Life Example 2 Step 1: Solve for k Using Half-Life Formula: h = - Ln 2 / k Subsitute in what we know: 5700 = -Ln 2 / k Solve for k: k - Ln 2 / 5700 k ≈ -0. 0001216 Step 2: Exponetial Form A(t) = A 0 ekt A(t) = A 0 e-. 0001216 t t = 1960 + 1346 (Note: 1346 B) t = 3306 A(3306) = A 0 e-. 0001216(3306) A(3306) ≈ 0. 66816 A 0

Half-Life Example 2 Step 3: Interpret Results What Percent of Carbon 14 Should be Left After 3306 Years? A(3306) ≈ 0. 66897 A 0 → 66. 897 % Since King Tut Ruled for 10 Years, What Percent of Carbon 14 Should be Left After 3366 Years? A(3316) = A 0 e-. 0001216(3316) A(3316) ≈ 0. 66816 A 0 → 66. 816 % Therefore, a piece of art made during King Tut’s time would have between 66. 816 % and 66. 897 % of its original carbon-14

Suggested Exercises Page 436: 81 - 83 and 89 - 93
 Growth and decay factors
Growth and decay factors Types of beta decay
Types of beta decay How to condense logs
How to condense logs Growth and decay formula
Growth and decay formula What is the difference between growth and decay
What is the difference between growth and decay Exponential growth and decay examples
Exponential growth and decay examples Rate of growth or decay
Rate of growth or decay Exponential growth and decay algebra 1
Exponential growth and decay algebra 1 Growth or decay exponential
Growth or decay exponential 6-3 lesson quiz exponential growth and decay
6-3 lesson quiz exponential growth and decay Exponential decay function
Exponential decay function Example of exponential growth equation
Example of exponential growth equation 9-3 exponential growth and decay
9-3 exponential growth and decay 7-7 exponential growth and decay
7-7 exponential growth and decay 7-1 exponential functions growth and decay
7-1 exponential functions growth and decay 4-1 exponential functions growth and decay
4-1 exponential functions growth and decay What is the difference between growth and decay
What is the difference between growth and decay Exponential growth and decay formula
Exponential growth and decay formula Exponential growth and decay practice
Exponential growth and decay practice 4-1 exponential functions growth and decay
4-1 exponential functions growth and decay 4-1 exponential functions growth and decay
4-1 exponential functions growth and decay Growth and decay
Growth and decay Exponential function form
Exponential function form Linear growth and decay
Linear growth and decay Identifying exponential growth and decay
Identifying exponential growth and decay Exponential differential equation
Exponential differential equation Geometric growth and decay
Geometric growth and decay Exponential growth and decay graphs
Exponential growth and decay graphs Exponential function
Exponential function Exponential decay vs growth
Exponential decay vs growth Exponential word problems examples
Exponential word problems examples Graph exponential function y=4^x
Graph exponential function y=4^x Growth or decay exponential
Growth or decay exponential Growth or decay exponential
Growth or decay exponential Plant growth definition
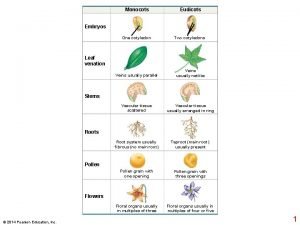
Plant growth definition Monocots eudicots
Monocots eudicots