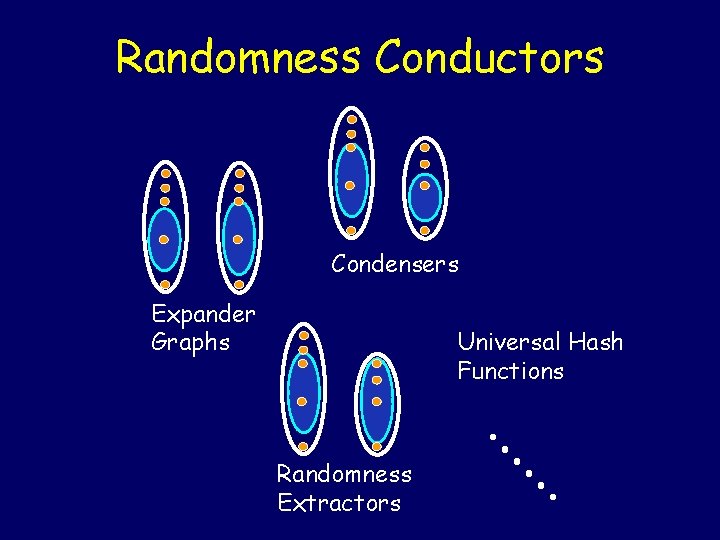
Randomness Conductors Condensers Expander Graphs Universal Hash Functions

Randomness Conductors Condensers Expander Graphs Universal Hash Functions Randomness Extractors . . .

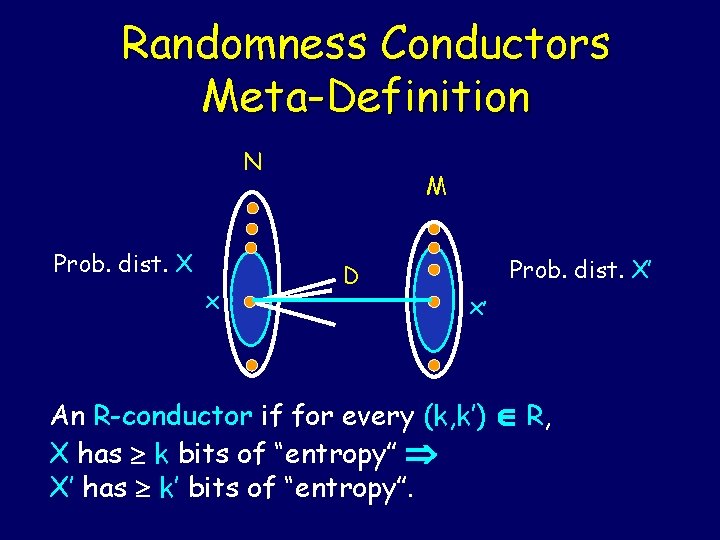
Randomness Conductors Meta-Definition N Prob. dist. X x M D Prob. dist. X’ x’ An R-conductor if for every (k, k’) R, X has k bits of “entropy” X’ has k’ bits of “entropy”.

Plan Definitions & Applications: • The balanced case (M = N). – Vertex Expansion. – 2 nd Eigenvalue Expansion. • The unbalanced case (M ≪ N). – Extractors, Dispersers, Condensers. Conductors • Universal Hash Functions. Constructions: • Zigzag Product & Loosless Expanders.

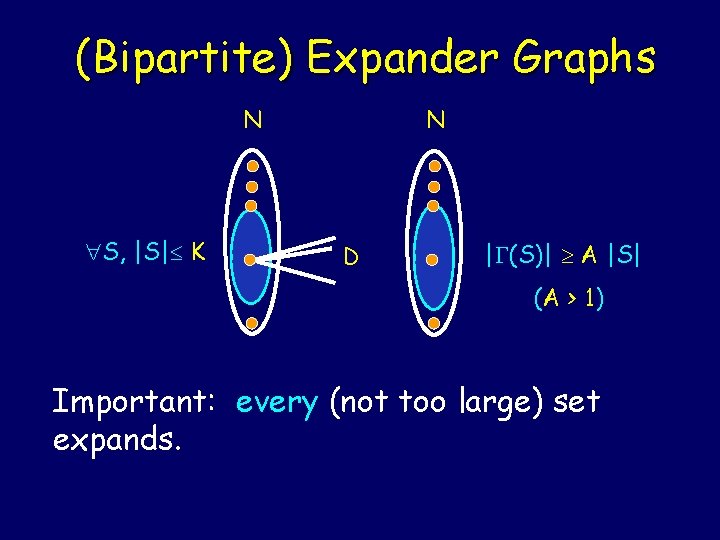
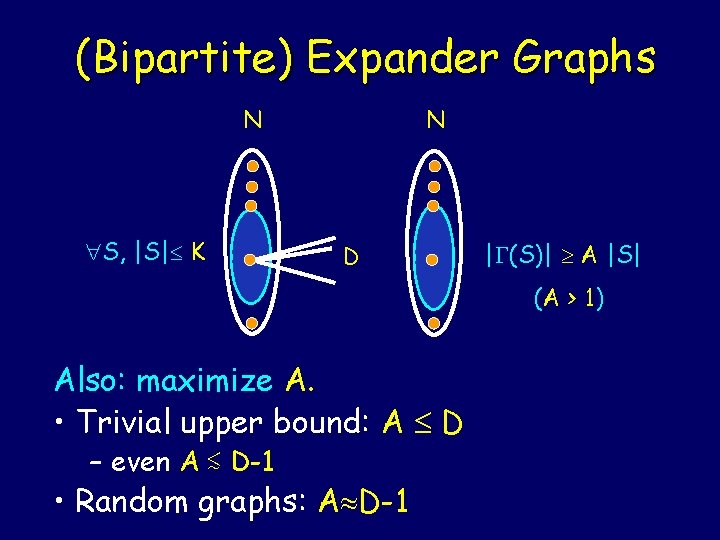
(Bipartite) Expander Graphs N S, |S| K N D | (S)| A |S| (A > 1) Important: every (not too large) set expands.

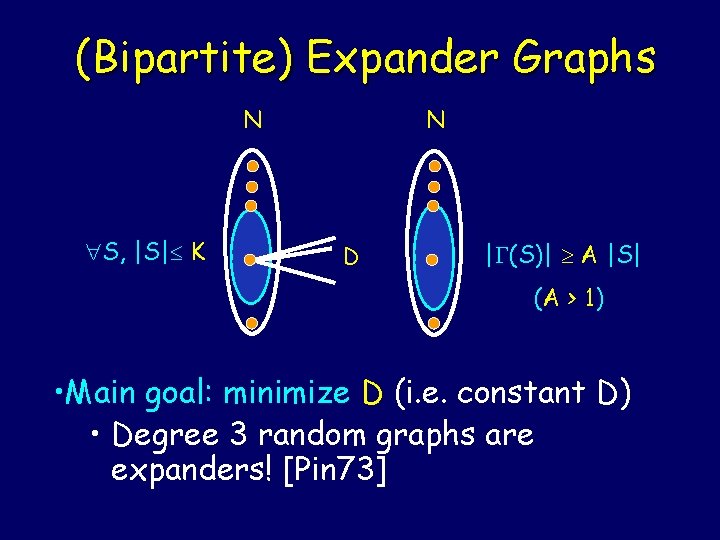
(Bipartite) Expander Graphs N S, |S| K N D | (S)| A |S| (A > 1) • Main goal: minimize D (i. e. constant D) • Degree 3 random graphs are expanders! [Pin 73]

(Bipartite) Expander Graphs N S, |S| K N D | (S)| A |S| (A > 1) Also: maximize A. • Trivial upper bound: A D – even A ≲ D-1 • Random graphs: A D-1

Applications of Expanders These “innocent” objects are intimately related to various fundamental problems: • • Network design (fault tolerance), Sorting networks, Complexity and proof theory, Derandomization, Error correcting codes, Cryptography, Ramsey theory And more. . .

Non-blocking Network with On-line Path Selection [ALM] N (Inputs) N (Outputs) Depth O(log N), size O(N log N), bounded degree. Allows connection between input nodes and output nodes using vertex disjoint paths.

Non-blocking Network with On-line Path Selection [ALM] N (Inputs) N (Outputs) Every request for connection (or disconnection) is satisfied in O(log N) bit steps: • On line. Handles many requests in parallel.

The Network N (Inputs) “Lossless” Expander

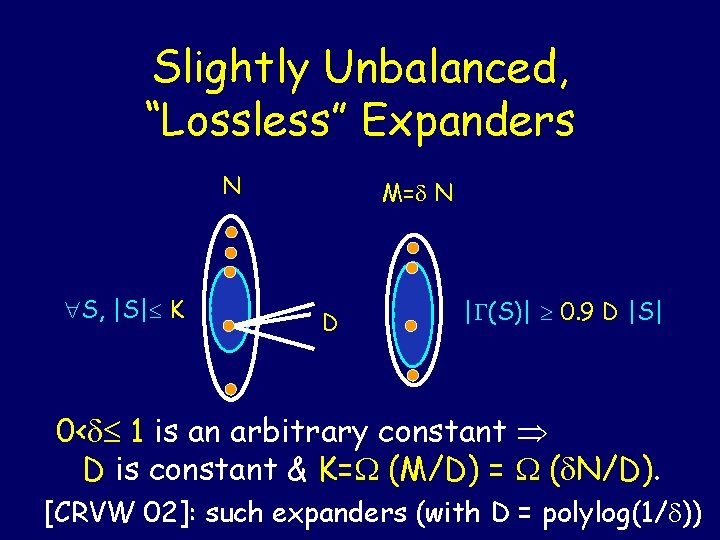
Slightly Unbalanced, “Lossless” Expanders N S, |S| K M= N D | (S)| 0. 9 D |S| 0< 1 is an arbitrary constant D is constant & K= (M/D) = ( N/D). [CRVW 02]: such expanders (with D = polylog(1/ ))

Property 1: A Very Strong Unique Neighbor Property S, |S| K, | (S)| 0. 9 D |S| S Unique neighbor of S Non Unique neighbor S has 0. 8 D |S| unique neighbors !

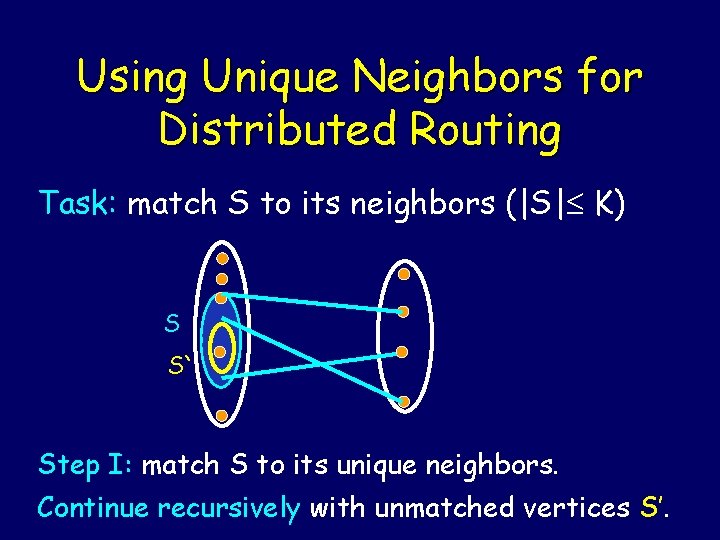
Using Unique Neighbors for Distributed Routing Task: match S to its neighbors (|S| K) S S` Step I: match S to its unique neighbors. Continue recursively with unmatched vertices S’.

Reminder: The Network Adding new paths: think of vertices used by previous paths as faulty.

Property 2: Incredibly Fault Tolerant S, |S| K, | (S)| 0. 9 D |S| Remains a lossless expander even if adversary removes (0. 7 D) edges from each vertex.

Simple Expander Codes [G 63, Z 71, ZP 76, T 81, SS 96] N (Variables) M= N (Parity Checks) 1 0 0 + + 1 +0 1 + Linear code; Rate 1 – M/N = (1 - ). Minimum distance K. Relative distance K/N= ( / D) = / polylog (1/ ). For small beats the Zyablov bound and is quite close to the Gilbert-Varshamov bound of / log (1/ ).

Simple Decoding Algorithm in Linear Time (& log n parallel phases) [SS 96] N (Variables) Error set B, |B| K/2 1 0 10 |FlipB| |B|/4 01 |BFlip| |B|/4 |Bnew| |B|/2 1 M= N (Constraints) + 0 + 1 | (B)| >. 9 D |B| 1 + 0 | (B) Sat|<. 2 D|B| + 0 • Algorithm: At each phase, flip every variable that “sees” a majority of 1’s (i. e, unsatisfied constraints).

Random Walk on Expanders [AKS 87] x 1 x 0 . . . x 2 xi xi converges to uniform fast (for arbitrary x 0). For a random x 0: the sequence x 0, x 1, x 2. . . has interesting “random-like” properties.

Expanders Add Entropy N Prob. dist. X x M D Induced dist. X’ x’ • Definition we gave: |Support(X’)| A |Support(X)| • Applications of the random walk rely on “less naïve” measures of entropy. • Almost all explicit constructions directly give “ 2 nd eigenvalue expansion”. • Can be interpreted in terms of Renyi entropy.

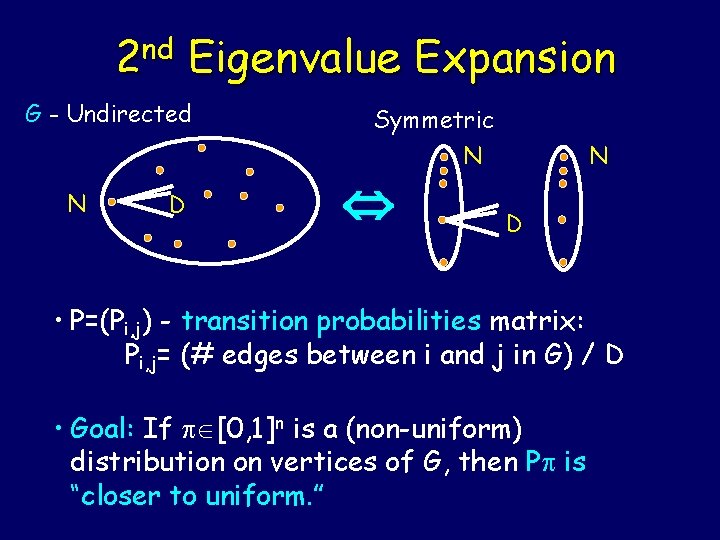
nd 2 Eigenvalue Expansion G - Undirected N D Symmetric N N D • P=(Pi, j) - transition probabilities matrix: Pi, j= (# edges between i and j in G) / D • Goal: If [0, 1]n is a (non-uniform) distribution on vertices of G, then P is “closer to uniform. ”

nd 2 Eigenvalue Expansion • 0 1 … N-1, eigenvalues of P. – 0 =1, Corresponding eigenvector v 0 =1 N: P(Uniform)=Uniform – Second eigenvalue (in absolute value): = (G)=max{| 1|, | N-1|} – G connected and non-bipartite <1 – is a good measure of the expansion of G [Tan 84, AM 84, Alo 86]. Qualitatively: G is an expander (G) < β < 1

Randomness Conductors • Expanders, extractors, condensers & hash functions are all functions, f : [N] [D] [M], that transform: X “of entropy” k X’ = f (X, Uniform) “of entropy” k’ • Many flavors: – Measure of entropy. – Balanced vs. unbalanced. – Lossless vs. lossy. – Lower vs. upper bound on k. – Is X’ close to uniform? – … Randomness conductors: As in extractors. Allows the entire spectrum.