Ramanujans verschachtelte Wurzeln Wann helfen Computer wann nicht

Ramanujans verschachtelte Wurzeln Wann helfen Computer, wann nicht?

Sriniwasa Ramanujan 1887 – 1920 � 1892 Einschulung Grundschule � 1897 erste Berührung mit Höherer Mathematik (Trigonometrie) � 1898 – 1904 High School � Keine Zulassung zum Studium Sicherung der Existenz mit Hilfe eines Gönners � 1913 Briefwechsel mit Hardy � 1914 Schiffsreise nach England � 1916 B. A. „Hochzusammengesetzte Zahlen“ � 1917 Aufnahme in die London Mathematical Society (erster Inder) � 1918 Wahl zum „Fellow of

1907 war das Gründungsjahr der Indian Mathematical Society, die ab 1910 vierteljährlich ein mathematisches Journal herausgab. Im Jahr 1911 stellte Ramanujan den Lesern des Journals die Frage nach der Größe der Zahl

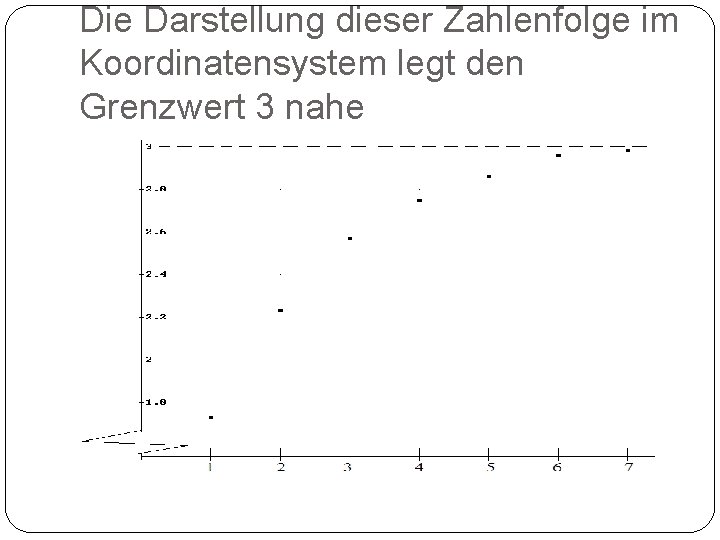
Ein halbes Jahr lang gingen keine Lösungsvorschläge ein, bis Ramanujan 3 Hefte später die Lösung verriet. Das ist verwunderlich, denn mit ein wenig Fleiß hätte auch ohne elektronisches Werkzeug die Aufstellung einer Zahlenfolge gelingen können :

Die Darstellung dieser Zahlenfolge im Koordinatensystem legt den Grenzwert 3 nahe

Ausgehend von der Hypothese, dass 3 die Lösung der Wurzelkette ist, ergeben sich sofort weitere Formeln:

Es gilt, zu beweisen �Induktionsanfang für n = 1 �Induktionsvoraussetzung für n = k: �Induktionsbehauptung für n = k+1 �Induktionsvoraussetzung quadrieren, 1 subtrahieren und durch (k-1) dividieren ergibt die Induktionsbehauptung �Aber. . .

Wie hat Ramanujan selbst seine Lösung verfasst? �Es gilt: �Definition einer Funktion f mit f(n)=n∙(n+2). �Dann gilt: �(i) f(n) = n ∙ (n + 2) = �(ii) f(n + 1) = (n + 1) ∙ (n + 3) = �(iii) f(n + 2) = (n + 2) ∙ (n + 4) = �(iv) f(n + 3) = (n + 3) ∙ (n + 5) = �Einsetzen „jeder“ Gleichung aus dieser Folge in ihren Vorgänger ergibt:

Das Verfahren lässt sich noch weiter verallgemeinern �Man wähle eine natürliche Zahl a und eine Polynomfunktion mit der Gleichung fa(x) = x 2+2 ax = x∙(x+2 a). �Es gilt x+a= = �und dann (x – a)∙(x + a) = (x – a) ∙ fa(x – a) = (x – a) ∙ (x + a) � fa(x – a) = (x – a) ∙

Setzen wir für x nacheinander die Werte der arithmetischen Folge x+a, x+2 a, x+3 a, … so erhalten wir: �und so weiter. �Jede Gleichung aus dieser Kette wird in ihren Vorgänger eingesetzt: �nach Division durch x (zur Erinnerung: )

Zum Abschluss noch eine etwas andere typische Ramanujan-Formel

Hier fällt auf: 28 = 98 = Ersetzen wir 7 durch a, so lautet Ramanujans Formel

Um diese Formel zu präzisieren, ist es nützlich auf beiden Seiten zu quadrieren, also insbesondere die Klammer zu quadrieren: � Da CAS berücksichtigt, dass dritte Wurzeln auch komplexe Lösungen haben können, wird als Quadrat (Klammer rechts) ein Mammut-ausdruck berechnet. Bei Beschränkung auf positive a liefert CAS � Von Hand vereinfacht zu � oder � Vollständig:

�An dieser Stelle zeigt ein Vergleich links und rechts des Gleichheitszeichens �und daher �und letztlich

Damit ist eine beliebig große Anzahl von Wurzelgleichungen des „ramanujanschen“ Typs gegeben. �Etwa für a = 4

Fazit �Beim Nachvollziehen von Ramanujans Gedankengängen oder bei Verallgemeinerungen seiner Zahlenbeispiele kann CAS nur geringe oder gar keine Beiträge leisten. �Potenzen mehrgliedriger Wurzelterme werden von CAS oft nicht mit einem Ergebnis ausgegeben, das zum Weiter-arbeiten erforderlich ist. �Ein spielerisches Hin- und Herspringen zwischen CAS-Einsatz und händischen Verfahren verspricht am meisten Erfolg. �Ohne Hand und Kopf hilft CAS nicht wirklich. CAS weiß nicht, wohin

Nun wird man einwenden, dass Ramanujans Formeln kein Schulstoff seien, deshalb sei ein Aufgabenvorschlag der Fachgruppe Computeralgebra der DMV, GI und GAMM angefügt. Berechne die Zahl mit den Taschenrechner. Vertraust Du dem Ergebnis? Könnte ein Rundungs- oder Rechenfehler vorliegen? Der Taschenrechner kann die Zusatzfragen nicht beantworten – das CAS ebenfalls nicht ohne Einsatz von Hand und Kopf.

Ich Danke Ihnen für Ihre Aufmerksamkeit Roland Schröder 29223 Celle Dehningstr. 26 florola@gmx. de