Quicksort 7 4 9 6 2 2 4

Quicksort 7 4 9 6 2 2 4 6 7 9 4 2 2 4 2 2 7 9 9 9

Brute Force – Algorithm Design Strategy • Brute force - A straightforward approach to solve a problem based directly on problem statement. o o Not particularly clever or efficient Usually intellectually easy to apply Use the force of the computer Still an important algorithm design strategy • Example Brute force sorts: o Selection sort o Bubble sort o Insertion sort Quicksort

Divide and Conquer –Algorithm Design Strategy • Divide and Conquero Divide - A problem is divided into smaller instances of the same problem, ideally the same size. • Smaller instances are solved(typically using recursion) • AKA recur o Conquer – Solutions to smaller instances of problems are combined to obtain a solution to original problem. • Example Divide and Conquer sorts: o Merge sort o Quick sort Quicksort

Outline • Quick-sort o o Algorithm Partition step Quick-sort tree Execution example • Average case intuition Quicksort

Quick-Sort • Randomized Quick-sorting algorithm is based on the divide-and-conquer paradigm: x o Divide: pick a random element x (called pivot) and partition S into • L elements less than x • E elements equal x • G elements greater than x o Recur: sort L and G o Conquer: join L, E and G Quicksort x L E x G

Quick-Sort Tree • An execution of quick-sort is depicted by a binary tree o Each node represents a recursive call of quicksort and stores • Unsorted sequence before the execution and its pivot • Sorted sequence at the end of the execution o The root is the initial call o The leaves are calls on subsequences of size 0 or 1 7 4 9 6 2 2 4 6 7 9 4 2 2 4 2 2 Quicksort 7 9 9 9

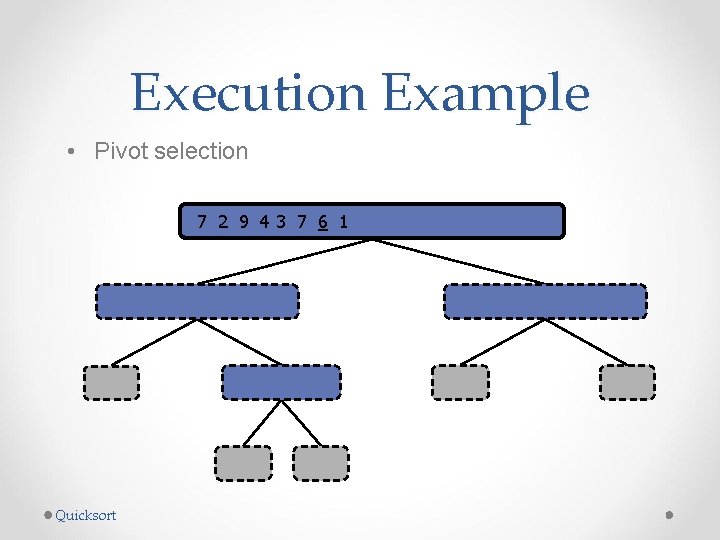
Execution Example • Pivot selection 7 2 9 43 7 6 1 1 2 3 4 6 7 8 9 7 2 9 4 2 4 7 9 2 2 9 4 4 9 9 9 Quicksort 3 8 6 1 1 3 8 6 4 4 3 3 8 8

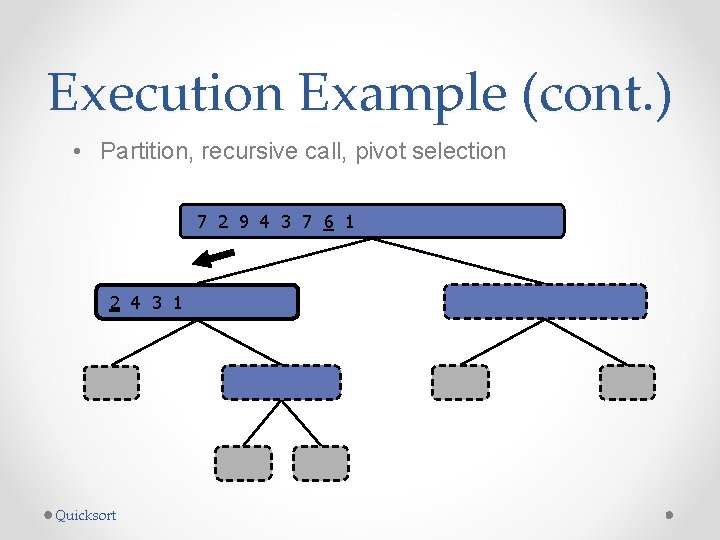
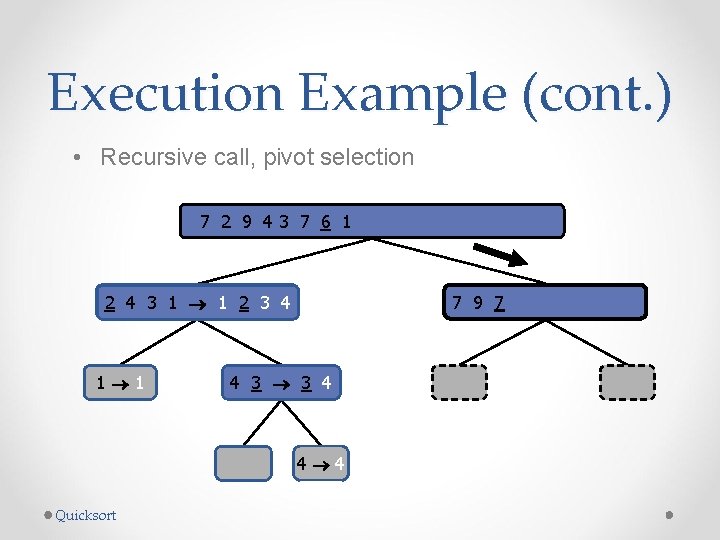
Execution Example (cont. ) • Partition, recursive call, pivot selection 7 2 9 4 3 7 6 1 1 2 3 4 6 7 8 9 2 4 3 1 2 4 7 9 2 2 9 4 4 9 9 9 Quicksort 3 8 6 1 1 3 8 6 4 4 3 3 8 8

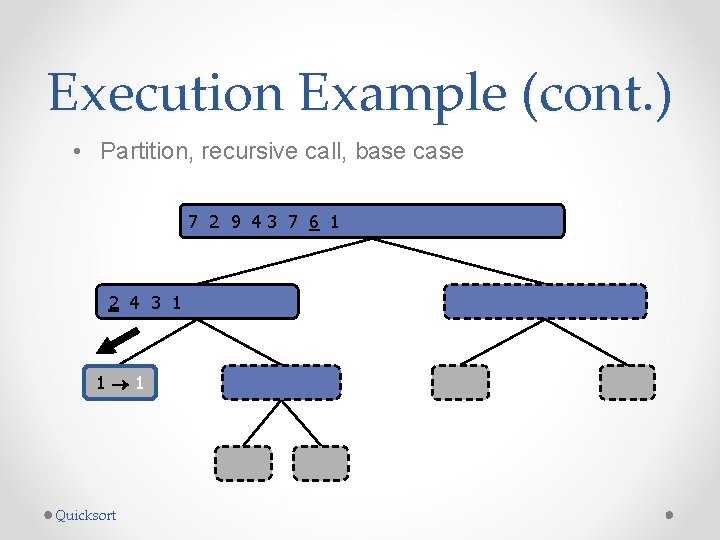
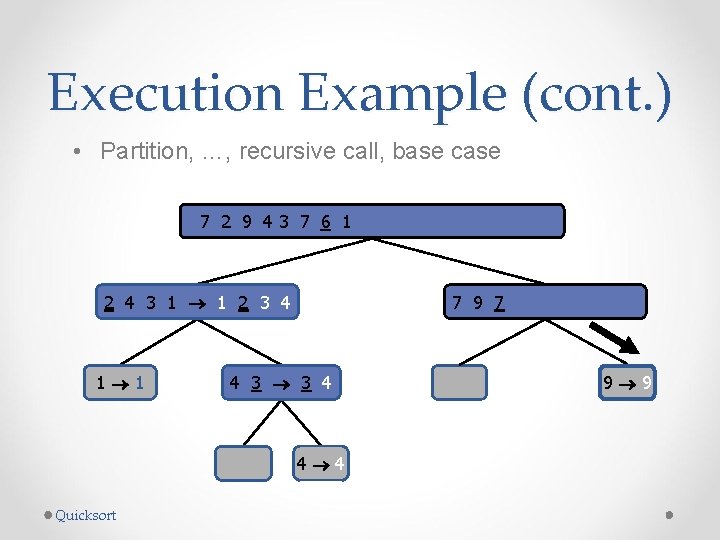
Execution Example (cont. ) • Partition, recursive call, base case 7 2 9 43 7 6 1 1 2 3 4 6 7 8 9 2 4 3 1 2 4 7 1 1 9 4 4 9 9 9 Quicksort 3 8 6 1 1 3 8 6 4 4 3 3 8 8

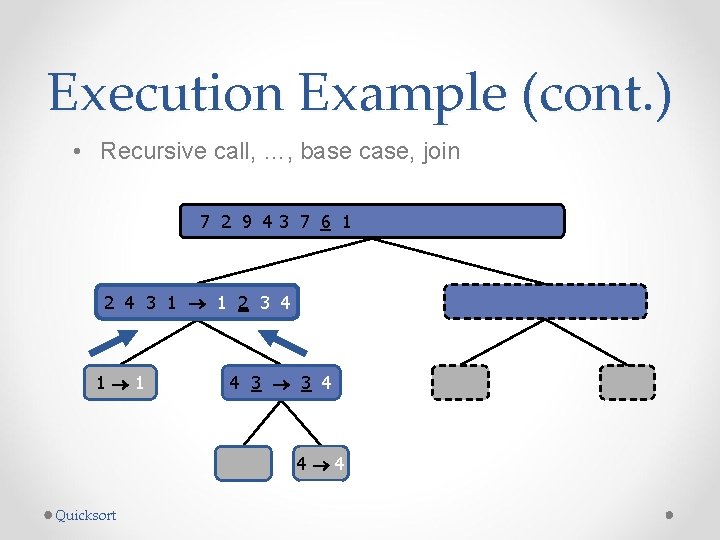
Execution Example (cont. ) • Recursive call, …, base case, join 7 2 9 43 7 6 1 1 2 3 4 6 7 8 9 2 4 3 1 1 2 3 4 1 1 4 3 3 4 9 9 Quicksort 3 8 6 1 1 3 8 6 4 4 3 3 8 8

Execution Example (cont. ) • Recursive call, pivot selection 7 2 9 43 7 6 1 1 2 3 4 6 7 8 9 2 4 3 1 1 2 3 4 1 1 4 3 3 4 9 9 Quicksort 7 9 7 1 1 3 8 6 4 4 8 8 9 9

Execution Example (cont. ) • Partition, …, recursive call, base case 7 2 9 43 7 6 1 1 2 3 4 6 7 8 9 2 4 3 1 1 2 3 4 1 1 4 3 3 4 9 9 Quicksort 7 9 7 1 1 3 8 6 4 4 8 8 9 9

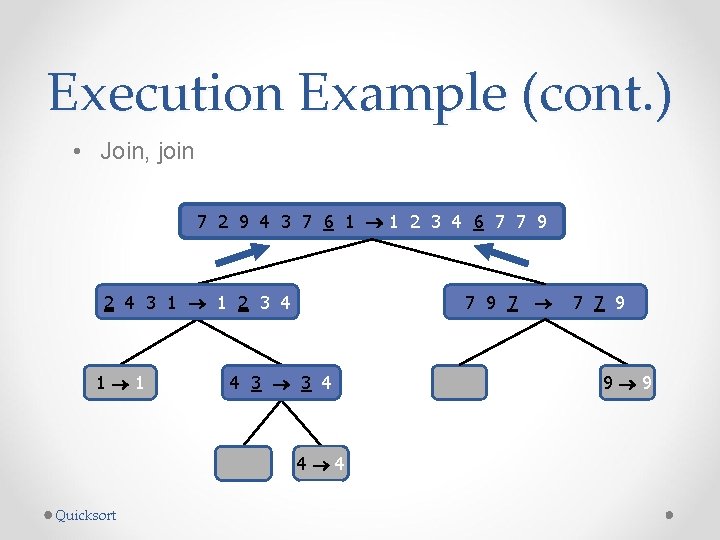
Execution Example (cont. ) • Join, join 7 2 9 4 3 7 6 1 1 2 3 4 6 7 7 9 2 4 3 1 1 2 3 4 1 1 4 3 3 4 9 9 Quicksort 7 9 7 17 7 9 4 4 8 8 9 9

Worst-case Running Time • The worst case for quick-sort occurs when the pivot is the unique minimum or maximum element • Either L and G has size n - 1 and the other has size 0 • The running time is proportional to the sum n + (n - 1) + … + 2 + 1 • Thus, the worst-case running time of quick-sort is O(n 2) depth time 0 n 1 n-1 … Quicksort … … n-1 1

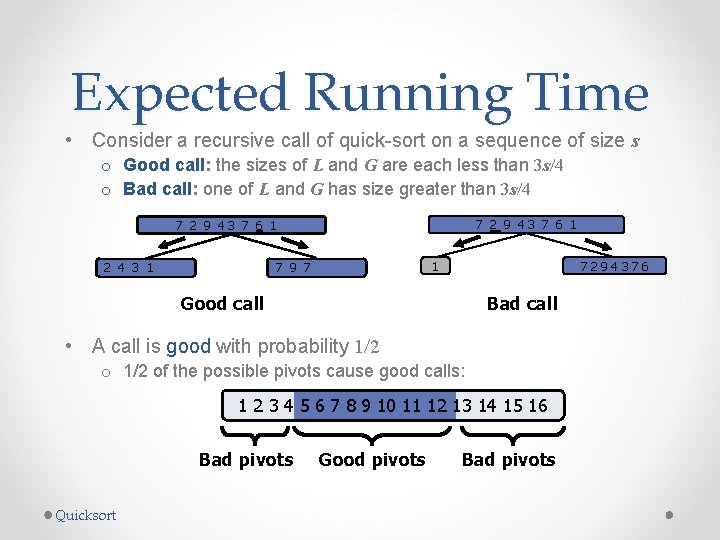
Expected Running Time • Consider a recursive call of quick-sort on a sequence of size s o Good call: the sizes of L and G are each less than 3 s/4 o Bad call: one of L and G has size greater than 3 s/4 7 2 9 43 7 6 19 7 1 1 2 4 3 1 1 7294376 Good call Bad call • A call is good with probability 1/2 of the possible pivots cause good calls: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 Bad pivots Quicksort Good pivots Bad pivots

Quicksort Implementation void quick. Sort( vector<Item>& v, int a, int b ) { // Let m be a guess as to the index of the median of the // items in v in the range v[a]. . . v[b] int M = v[m]; swap( v[m], v[b] ) int L = a; int R = b-1; while ( L <= R ) { while ( v[L] < M ) ++L; while ( v[R] > M ) --R; if ( L < R ) swap( v[L], v[R] ); } swap ( v[b], v[R] ); // putting M in between quick. Sort( v, a, L ); quick. Sort( v, R+1, b ); } Quicksort