Sorting Techniques Introduction Sorting algorithm specifies the way

Sorting Techniques

Introduction Sorting algorithm specifies the way to arrange data in a particular order. Most common orders are numerical or lexicographical order. Sorting is also used to represent data in more readable formats. Telephone Directory − Telephone directory keeps telephone no. of people sorted on their names. Dictionary − Dictionary keeps words in alphabetical order so that searching of any work becomes easy.

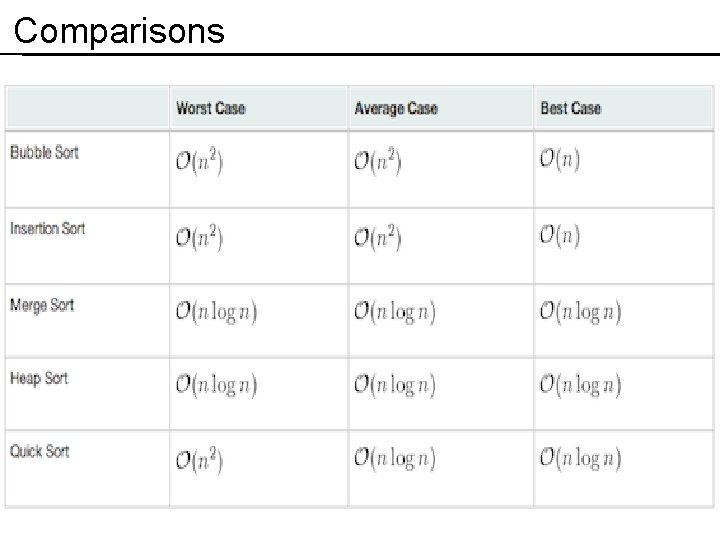
Sorting Algorithms Internal Sorting – sorting takes place in main memory External Sorting – external memory is needed for sorting Internal Sorting Bubble sort, Insertion sort, Selection Sort - O(n 2) Shell sort - less than O(n 2) Merge Sort – O(n log n) (both average and worst case) Quick sort - O(n log n) (average case) O(n 2) (worst case) Heap sort - O(n log n)

Bubble Sort Bubble sort is a simple sorting algorithm. This sorting algorithm is comparison based algorithm in which each pair of adjacent elements is compared and elements are swapped if they are not in order. This algorithm is not suitable for large data sets as its average and worst case complexity are of O(n 2) where n are no. of items.

Bubble Sort begin Bubble. Sort(list) for i=0 to n do for j=0 to n do if list[j] > list[j+1] swap(list[j], list[j+1]) end if end for return list end Biggest element is moved to the last position in the 1 st iteration Second bigger number is moved to last but one position in the 2 nd iteration http: //www. tutorialspoint. com/data_structures_algorithms/bubble_sort_algorithm. ht m

Insertion Sort This is a in-place comparison based sorting algorithm. Here, a sub-list is maintained which is always sorted. For example, the lower part of an array is maintained to be sorted. A element which is to be 'insert'ed in this sorted sub-list, has to find its appropriate place and insert it there. Hence the name insertion sort. The array is searched sequentially and unsorted items are moved and inserted into sorted sub-list (in the same array). This algorithm is not suitable for large data sets as its average and worst case complexity are of Ο(n 2) where n are no. of items.

Insertion Sort Begin insertion. Sort(list) for (i=1; i < n ; i++ ) temp=a[i]; for (j=i; j > 0 && temp < a[j-1]; j-- ) a[j]=a[j-1]; end for a[j]=temp; end for return list end At ith iteration, all i-1 Elements are sorted https: //en. wikipedia. org/wiki/Insertion_sort http: //www. tutorialspoint. com/data_structures_algorithms/insertion_sort_algorithm. htm http: //www. cs. armstrong. edu/liang/animation/web/Insertion. Sort. html

Differences – Bubble sort and Insertion sort Number of iterations of inner loop of insertion sort is less compared to bubble sort. Number of assignments inside the inner loop is also 1. Insertion Sort After i iterations the first i elements are ordered. In each iteration the next element is bubbled through the sorted section until it reaches the right spot: sorted | unsorted 1358|46792 13458|6792 The 4 is bubbled into the sorted section Bubble Sort After i iterations the last i elements are the biggest, and ordered. In each iteration, sift through the unsorted section to find the maximum. unsorted | biggest 31542|6789 1342|56789 The 5 is bubbled out of the unsorted section

Shell Sort Shell sort is a highly efficient sorting algorithm and is based on insertion sort algorithm. This algorithm avoids large shifts as in case of insertion sort if smaller value is very far right and have to move to far left. This algorithm uses insertion sort on widely spread elements first to sort them and then sorts the less widely spaced elements. This spacing is termed as interval. This algorithm is quite efficient for medium sized data sets as its average and worst case complexity are of O(n 1. 5) where n are no. of items. Diminishing incremental sorting

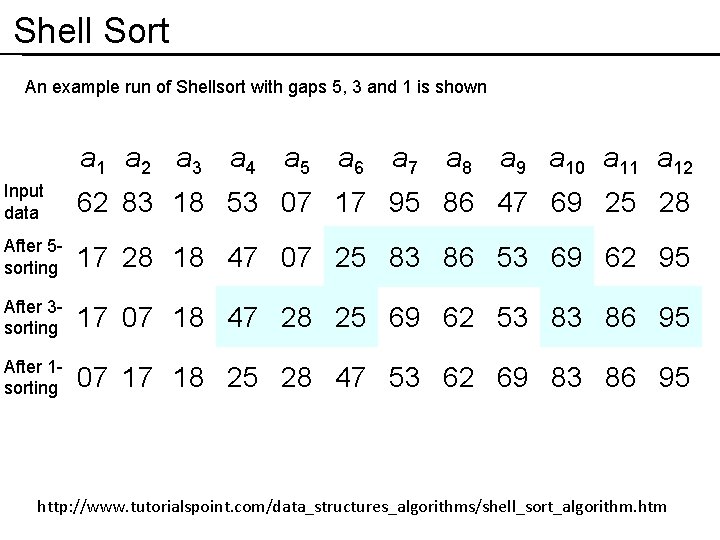
Shell Sort An example run of Shellsort with gaps 5, 3 and 1 is shown a 1 a 2 a 3 a 4 a 5 a 6 a 7 a 8 a 9 a 10 a 11 a 12 Input data 62 83 18 53 07 17 95 86 47 69 25 28 After 5 sorting 17 28 18 47 07 25 83 86 53 69 62 95 After 3 sorting 17 07 18 47 28 25 69 62 53 83 86 95 After 1 sorting 07 17 18 25 28 47 53 62 69 83 86 95 http: //www. tutorialspoint. com/data_structures_algorithms/shell_sort_algorithm. htm

Shell Sort begin shell. Sort(list) for (gap = n/2; gap > 0; gap=gap/2) for (i = gap; i< n; i++) temp = list[i]; j = i; while ( j >= gap && temp < list[j – gap] ) list[j] = list[j-gap]; j-= gap; end while list[j] = temp; end for end Animation is at: https: //www. youtube. com/watch? v=qz. XAVXddc. PU

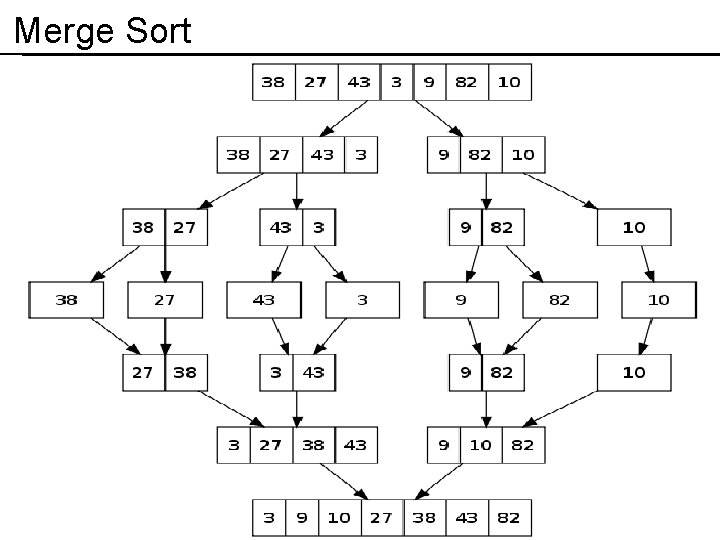
Merge Sort Mergesort is a divide and conquer algorithm First divide the list into the smallest unit (1 element), Compare each element with the adjacent list to sort and merge the two adjacent lists. Finally all the elements are sorted and merged. Conceptually, a merge sort works as follows: 1. Divide the unsorted list into n sublists, each containing 1 element (a list of 1 element is considered sorted). 2. Repeatedly merge sublists to produce new sorted sublists until there is only 1 sublist remaining. This will be the sorted list.

Merge Sort

Merge Sort mergesort(int left, int right) { int center; if(left<right) { center=(left+right)/2; mergesort(left, center); mergesort(center+1, right); merge(left, center+1, right); } } https: //en. wikipedia. org/wiki/Merge_sort https: //www. youtube. com/watch? v=IR 7 DFDej 6 l 4

Merge Sort void merge(int lp, int re) { lend = rp-1; tp=lp; n=rend +1; while(lp<=lend && rp<=rend) { if(a[lp]<=a[rp]) tempa[tp]=a[lp++]; else tempa[tp]=a[rp++]; tp++; } while(lp<=lend) tempa[tp++]=a[lp++]; while(rp<=rend) tempa[tp++]=a[rp++]; for(i=0; i<n; i++) a[i]=tempa[i]; }

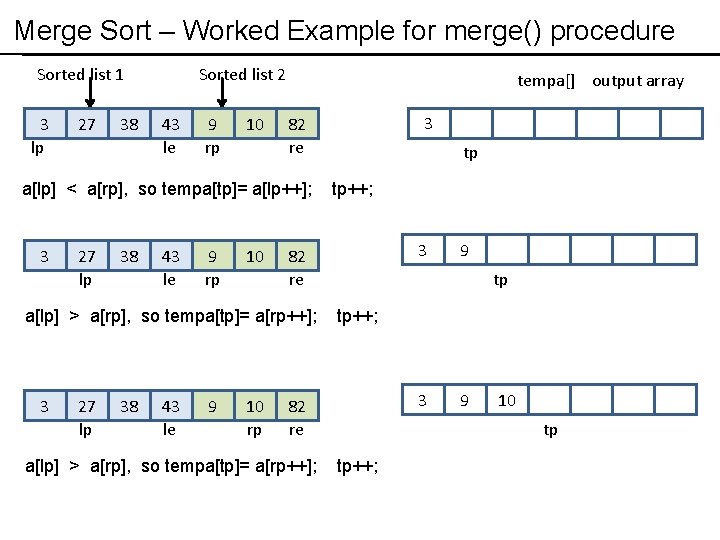
Merge Sort – Worked Example for merge() procedure Sorted list 1 3 lp 27 38 Sorted list 2 43 le 9 rp 10 tempa[] output array a[lp] < a[rp], so tempa[tp]= a[lp++]; 3 27 lp 38 43 le 9 rp 10 27 lp 38 43 le 9 10 rp tp tp++; 3 82 re a[lp] > a[rp], so tempa[tp]= a[rp++]; 3 3 82 re tp tp++; 3 82 re a[lp] > a[rp], so tempa[tp]= a[rp++]; 9 9 10 tp tp++;

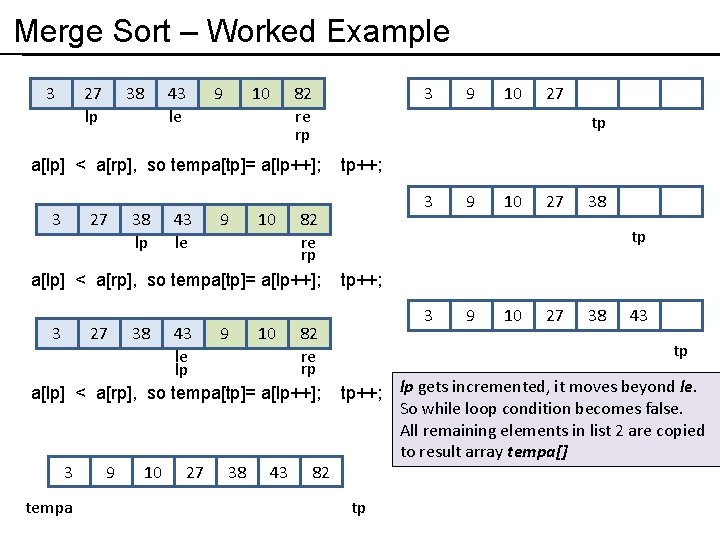
Merge Sort – Worked Example 3 27 lp 38 43 le 9 10 82 re rp a[lp] < a[rp], so tempa[tp]= a[lp++]; 3 27 38 lp 43 le 9 tempa 9 27 38 43 82 10 27 tp++; 3 9 10 27 38 tp tp++; 3 38 10 9 tp 10 43 9 10 82 le re rp lp a[lp] < a[rp], so tempa[tp]= a[lp++]; 3 3 9 10 27 38 43 tp tp++; lp gets incremented, it moves beyond le. So while loop condition becomes false. All remaining elements in list 2 are copied to result array tempa[] tp

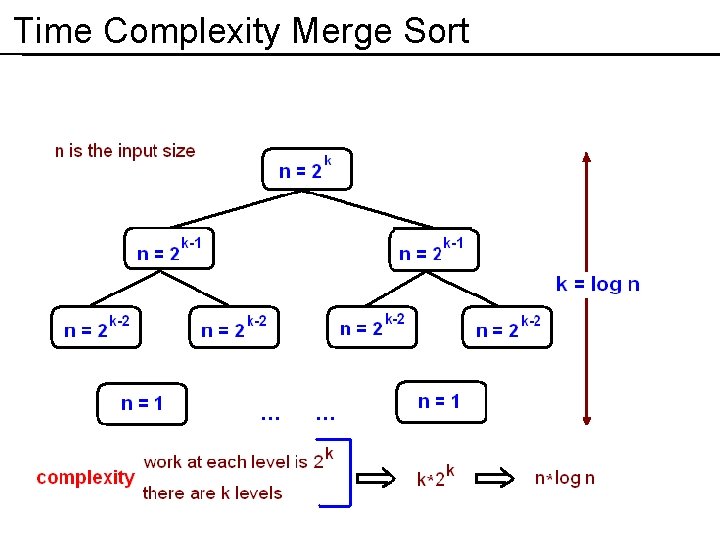
Time Complexity Merge Sort

Quick Sort Quicksort is a divide and conquer algorithm Quicksort (or partition-exchange sort) is an efficient sorting algorithm, serving as a systematic method for placing the elements of an array in order. When implemented well, it can be about two or three times faster than its main competitors, merge sort and heapsort. - Quicksort first divides a large array into two smaller sub-arrays: the low elements and the high elements. - Quicksort can then recursively sort the sub-arrays.

Quick Sort The steps are: 1. Pick an element, called a pivot, from the array. 2. Partitioning: reorder the array so that all elements with values less than the pivot come before the pivot, while all elements with values greater than the pivot come after it (equal values can go either way). After this partitioning, the pivot is in its final position. This is called the partition operation. 3. Recursively apply the above steps to the sub-array of elements with smaller values and separately to the sub-array of elements with greater values. The pivot selection and partitioning steps can be done in several different ways; the choice of specific implementation schemes greatly affects the algorithm's performance.

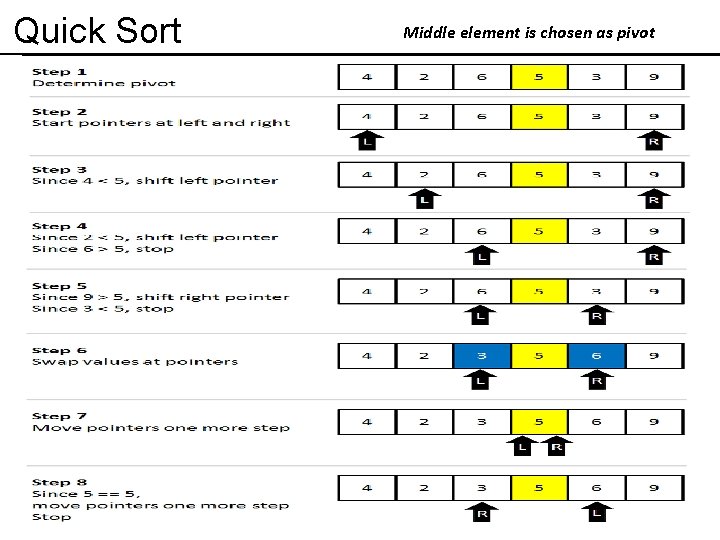
Quick Sort Middle element is chosen as pivot

Quick Sort void quick. Sort(int a[], int l, int r) { int pivot, i, j; if(l<=r) { pivot = a[r]; // last element as pivot i=l; j=r-1; while(i<=j) // for (; ; ) can also be used, break takes care { while(a[i]< pivot) i++; while(a[j]> pivot) j--; if(i< j) swap(elements at i and j position); else break; } swap ( ith element and rth element)// to restore pivot quicksort(a, l, i-1); quicksort(a, i+1, r); }

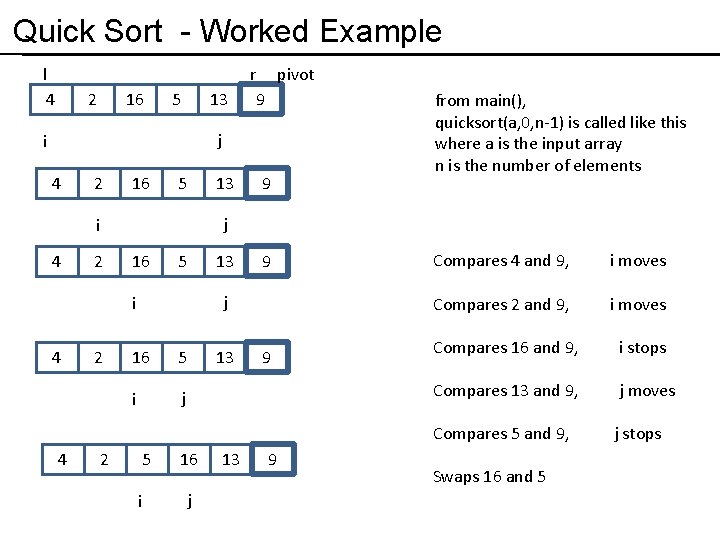
Quick Sort - Worked Example l 4 2 16 5 13 r pivot 9 j i 4 2 16 5 4 2 2 13 9 j i 4 13 from main(), quicksort(a, 0, n-1) is called like this where a is the input array n is the number of elements 16 5 i j 5 i 16 j 13 13 9 9 Compares 4 and 9, i moves Compares 2 and 9, i moves Compares 16 and 9, i stops Compares 13 and 9, j moves Compares 5 and 9, j stops Swaps 16 and 5

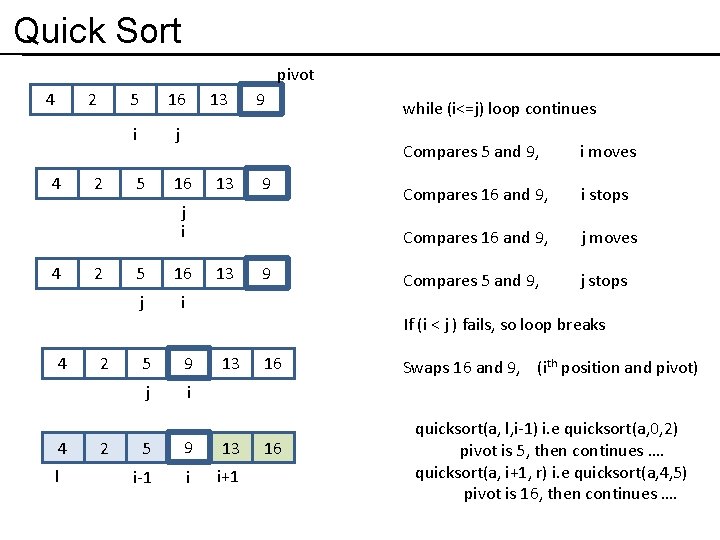
Quick Sort pivot 4 2 5 16 13 i j 5 16 13 9 9 j i 4 4 4 l 2 2 2 5 16 j i 5 9 j i 13 9 while (i<=j) loop continues Compares 5 and 9, i moves Compares 16 and 9, i stops Compares 16 and 9, j moves Compares 5 and 9, j stops If (i < j ) fails, so loop breaks 13 5 9 13 i-1 i i+1 16 16 Swaps 16 and 9, (ith position and pivot) quicksort(a, l, i-1) i. e quicksort(a, 0, 2) pivot is 5, then continues …. quicksort(a, i+1, r) i. e quicksort(a, 4, 5) pivot is 16, then continues ….

Comparisons