Probabilistic Reasoning and Bayesian Belief Networks 1 Bayes

Probabilistic Reasoning and Bayesian Belief Networks 1

Bayes Classifier n A probabilistic framework for solving classification problems Probability of an even A Conditional Probability: n P(A ∧ C) = P(A|C)P(C), P(A ∧ C) = P(C|A)P(A) n n P(C|A)P(A) = P(A|C)P(C) Bayes theorem:

Example of Bayes Theorem n Given: n n A doctor knows that meningitis causes stiff neck 50% of the time Prior probability of any patient having meningitis is 1/50, 000 Prior probability of any patient having stiff neck is 1/20 If a patient has stiff neck, what’s the probability he/she has meningitis?

Example 2 n n n When one has a cold, one usually has a high temperature (let us say, 80% of the time). We can use A to denote “I have a high temperature” and B to denote “I have a cold. ” Therefore, we can write this statement of posterior probability as P(A|B) = 0. 8. Now, let us suppose that we also know that at any one time around 1 in every 10, 000 people has a cold, and that 1 in every 1000 people has a high temperature. We can write these prior probabilities as P(A) = 0. 001, P(B) = 0. 0001 Now suppose that you have a high temperature. What is the likelihood that you have a cold? This can be calculated very simply by using Bayes’ theorem: 30 September 2020 4

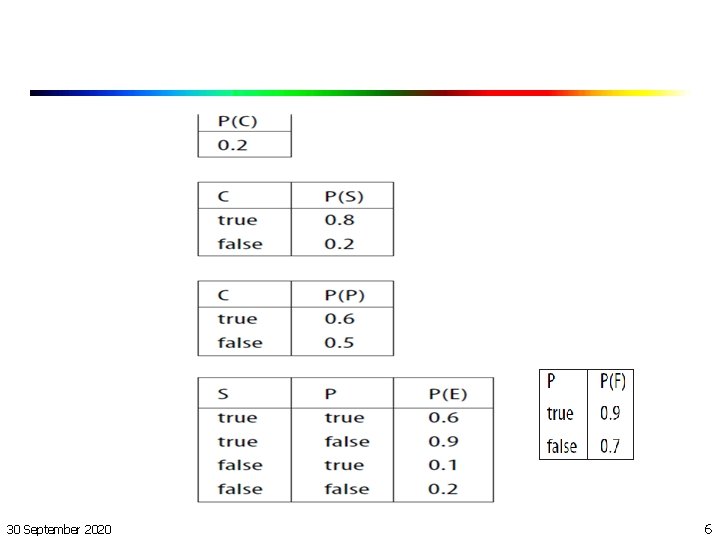
Bayesian Belief Networks n n n Example: Life at College C = that you will go to college S = that you will study P = that you will party E = that you will be successful in your exams F = that you will have fun 30 September 2020 5

30 September 2020 6

30 September 2020 7

30 September 2020 8

Bayesian Classifiers n Consider each attribute and class label as random variables n Given a record with attributes (A 1, A 2, …, An) n n n Goal is to predict class C Specifically, we want to find the value of C that maximizes P(C| A 1, A 2, …, An ) Can we estimate P(C| A 1, A 2, …, An ) directly from data?

Bayesian Classifiers n Approach: n compute the posterior probability P(C | A 1, A 2, …, An) for all values of C using the Bayes theorem n n n Choose value of C that maximizes P(C | A 1, A 2, …, An) Equivalent to choosing value of C that maximizes P(A 1, A 2, …, An|C) P(C) How to estimate P(A 1, A 2, …, An | C )?

Naïve Bayes Classifier n Assume independence among attributes Ai when class is given: n P(A 1, A 2, …, An |C) = P(A 1| Cj) P(A 2| Cj)… P(An| Cj) n Can estimate P(Ai| Cj) for all Ai and Cj. n New point is classified to Cj if P(Cj) P(Ai| Cj) is maximal.

Example of Naïve Bayes Classifier A: attributes M: mammals N: non-mammals P(A|M)P(M) > P(A|N)P(N) => Mammals

Naïve Bayesian Classifier: Training Dataset Class: C 1: buys_computer = ‘yes’ C 2: buys_computer = ‘no’ Data sample X = (age <=30, Income = medium, Student = yes Credit_rating = Fair) 30 September 2020 13

Naïve Bayesian Classifier: An Example n P(Ci): n Compute P(X|Ci) for each class P(buys_computer = “yes”) = 9/14 = 0. 643 P(buys_computer = “no”) = 5/14= 0. 357 P(age = “<=30” | buys_computer = “yes”) = 2/9 = 0. 222 P(age = “<= 30” | buys_computer = “no”) = 3/5 = 0. 6 P(income = “medium” | buys_computer = “yes”) = 4/9 = 0. 444 P(income = “medium” | buys_computer = “no”) = 2/5 = 0. 4 P(student = “yes” | buys_computer = “yes) = 6/9 = 0. 667 P(student = “yes” | buys_computer = “no”) = 1/5 = 0. 2 P(credit_rating = “fair” | buys_computer = “yes”) = 6/9 = 0. 667 P(credit_rating = “fair” | buys_computer = “no”) = 2/5 = 0. 4 n X = (age <= 30 , income = medium, student = yes, credit_rating = fair) P(X|Ci) : P(X|buys_computer = “yes”) = 0. 222 x 0. 444 x 0. 667 = 0. 044 P(X|buys_computer = “no”) = 0. 6 x 0. 4 x 0. 2 x 0. 4 = 0. 019 P(X|Ci)*P(Ci) : P(X|buys_computer = “yes”) * P(buys_computer = “yes”) = 0. 028 P(X|buys_computer = “no”) * P(buys_computer = “no”) = 0. 007 Therefore, X belongs to class (“buys_computer = yes”) 30 September 2020 14

Naïve Bayes (Summary) n n Robust to isolated noise points Handle missing values by ignoring the instance during probability estimate calculations Robust to irrelevant attributes Independence assumption may not hold for some attributes n Use other techniques such as Bayesian Belief Networks (BBN)