Piirteoreemid Piirteoreemide koht tenosusteoorias Teoreeme mis seovad massiliselt

Piirteoreemid

Piirteoreemide koht tõenäosusteoorias Teoreeme, mis seovad massiliselt esinevate juhuslike nähtuste teoreetilisi ja eksperimentaalseid karakteristikuid, tuntakse tõenäosusteooria piirteoreemidena. Piirteoreeme on kahte liiki: 1. Suurte arvude seadus Juhuslike nähtuste karakteristikute (näiteks keskväärtuse) omadus katsete arvu kasvades läheneda mingitele konstantidele - Tšebõševi teoreem - Bernoulli teoreem 2. Tsentraalne piirteoreem e. Ljapunovi teoreem Tingimused juhuslike suuruste jada koondumiseks normaaljaotuseks.

Tõenäosuse järgi koondumine Öeldakse, et juhuslike suuruste jada X 1, X 2, . . . koondub tõenäosuse järgi juhuslikuks suuruseks X, kui iga e > 0 korral Täpsemalt väljendudes: Öeldakse, et juhuslike suuruste jada X 1, X 2, . . . koondub tõenäosuse järgi juhuslikuks suuruseks X, kui iga e > 0 ja d > 0 korral leidub n = n(e, d), millest alates kehtib võrratus Tõenäosuse järgi koondumine tähendab seda, et tõenäosus juhuslike suuruste Xn ja X oluliseks erinemiseks läheneb nullile ehk seda esineb väga harva. Juhuslike suuruste jada {Xn} piirväärtuseks võib olla ka triviaalne juhuslik suurus – konstant.

Tšebõševi suurte arvude seadus (1867) Küllalt suure arvu võrdsete keskväärtuste EX ja võrdsete dispersioonidega sõltumatute juhuslike suuruste X 1, X 2, . . . , Xn puhul läheneb nende suuruste aritmeetiline keskmine tõenäosuse järgi keskväärtusele: iga e > 0 korral Selles teoreemis ei väideta absoluutse kindlusega, et , vaid tõenäosuse järgi. Ka suure hulga juhuslike suuruste aritmeetiline keskmine võib oluliselt hälbida keskväärtusest, kuid seda juhtub väga harva, s. t. suurte hälvete tõenäosus läheneb nullile. Tšebõševi suurte arvude seadus on kinnituseks sellele, et katseliselt määratava suuruse tõelise väärtuse parimaks lähendiks on katsetulemuste aritmeetiline keskmine ja viimane on seda usaldusväärsem, mida pikema katseseeria põhjal see on leitud.

Bernoulli suurte arvude seadus (1713) Korduvatel sõltumatutel katsetel koondub sündmuse suhteline sagedus katsete arvu n kasvamisel tõenäosuse järgi sündmuse tõenäosuseks: kus m on sündmuse toimumiskordade arv katseseerias ja e > 0 kuitahes väike positiivne arv. Teisiti öeldes: sündmuse suhteline sagedus koondub tõenäosuse järgi selle sündmuse tõenäosuseks üksikkatsel. Bernoulli suurte arvude seadus kinnitab, et suhteline sagedus küllalt pikas katseseerias e. nn. statistiline tõenäosus sobib sündmuse tõenäosuse hinnanguks.

Ljapunovi teoreem (tsentraalne piirteoreem) Olgu juhuslik suurus X küllalt suure hulga n sõltumatu juhusliku suuruse Xi (i = 1, . . . , n) summa: Osasuuruste Xi jaotusseadused võivad olla väga erinevad, kuid iga osasuuruse osatähtsus summaarse juhusliku suuruse X moodustamisel olgu väike. Siis läheneb summaarse juhusliku suuruse X jaotus normaaljaotusele liidetavate arvu n kasvamisel. Näide Ljapunovi teoreem annab seletuse, miks rakendustes kasutatakse kõige sagedamini normaaljaotusega või sellele lähedase jaotusega suurusi. Nii näiteks allub juhuslik mõõtmisviga normaaljaotusele. Mõõtmisviga moodustub paljude juhuslike põhjuste koosmõjul, kus iga üksikpõhjus tingib summaarse vea seisukohalt tühise vea. Vea komponentide põhjustajate hulk on tavaliselt suur.

Moivre – Laplace‘i integraalne piirteoreem Kui m on sündmuse A toimumiste arv n sõltumatu katse korral ja sündmuse A tõenäosus p on jääv, siis kehtib valem (1) kus q = 1 – p ja F(x) on Laplace‘i funktsioon. Valem (1) on teisendatav praktikas sagedasemat kasutamist leidvale kujule: See valem võimaldab küllalt suure katsete arvu korral kasutada diskreetse binoomjaotuse asemel ligikaudse lähendina pidevat normaaljaotust parameetritega EX = np ja s(X) =

Moivre – Laplace‘i lokaalne piirteoreem Katsete arvu n tõkestamatul kasvamisel koondub binoomjaotus normaaljaotuseks parameetritega EX = np ja s(X) = Seega küllalt suure katsete arvu korral võime sündmuse sageduse m tõenäosuse arvutamiseks kasutada Bernoulli valemi asemel ligikaudset valemit normeeritud normaaljaotuse tihedusfunktsioon Valemi kasutamine on õigustatud kui 1) np > 5 või 2) nq > 5.

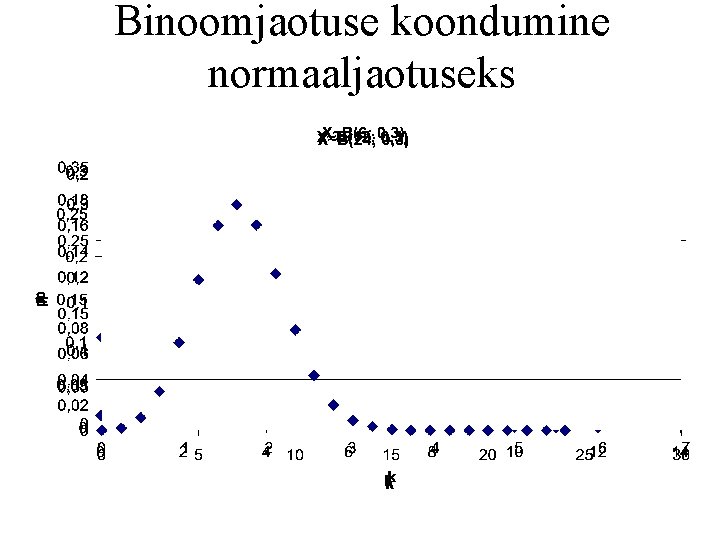
Binoomjaotuse koondumine normaaljaotuseks

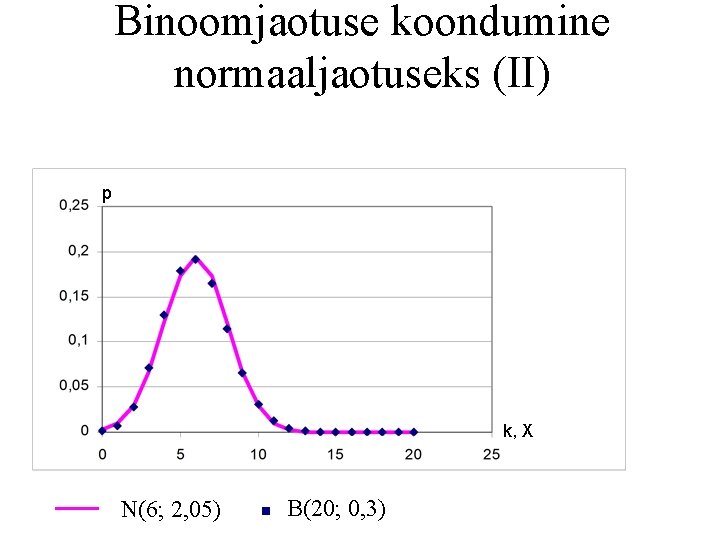
Binoomjaotuse koondumine normaaljaotuseks (II) p k, X N(6; 2, 05) B(20; 0, 3)

Näide Münti visatakse 50 korda. Kui tõenäone on 1) vapi esinemine 20 korda; 2) vapi esinemissageduse asumine 20 ja 28 vahel? Lahendus Vapi tõenäosus üksikkatsel p = 0, 5 ja ka q = 0, 5. Seega np = 25 ja npq = 12, 5, . 1) 2)