Optimizing a function means taking into account all

Optimizing a function means taking into account all of the resources and limitations and getting the greatest benefit. With all the considerations you try to use them to the greatest effect. Efficiency and economy are words that you should think of when optimizing a function. It is necessary to analyze the constraints as they relate to each other and a very effective way to do this is by constructing a POLYGON OF CONSTRAINTS. The polygon is formed through the intersection of all of the constraints. Depending on the number of constraints and their relationship to each other the polygon can be a triangle, a quadrilateral, a pentagon and so on.

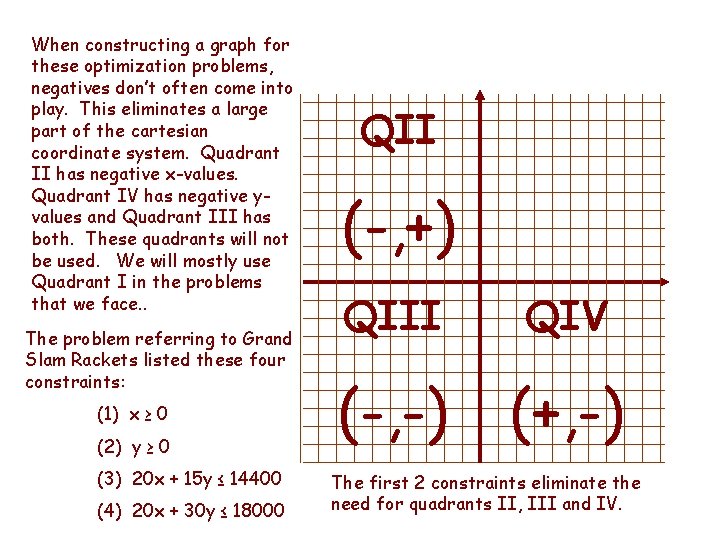
When constructing a graph for these optimization problems, negatives don’t often come into play. This eliminates a large part of the cartesian coordinate system. Quadrant II has negative x-values. Quadrant IV has negative yvalues and Quadrant III has both. These quadrants will not be used. We will mostly use Quadrant I in the problems that we face. . The problem referring to Grand Slam Rackets listed these four constraints: (1) x ≥ 0 (2) y ≥ 0 (3) 20 x + 15 y ≤ 14400 (4) 20 x + 30 y ≤ 18000 QII (-, +) QIII QIV (-, -) (+, -) The first 2 constraints eliminate the need for quadrants II, III and IV.

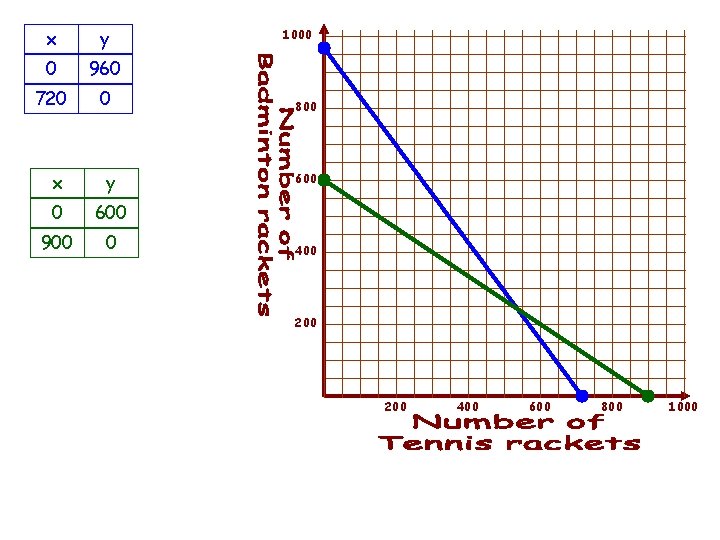
Using only Quadrant I now eliminates the need to refer to the first 2 constraints. The x and y axes serve as the boundaries for those constraints. (1) x ≥ 0 To construct the graph for constraints that have both variables, the simplest thing to do might be to find the x and y intercepts for each. (3) 20 x + 15 y ≤ 14400 15 y = 14400 (3) 20 x + 15 y ≤ 14400 960 720 0 20 x + 15(0) = 14400 (4) 20 x + 30 y ≤ 18000 20 x = 14400 20(0) + 30 y = 18000 x = 720 (720, 0) 30 y = 18000 y = 600 (0, 600) y = 900 (900, 0) 0 y = 960 (0, 960) (4) 20 x + 30 y ≤ 18000 20 x = 18000 y 20(0) + 15 y = 14400 (2) y ≥ 0 20 x + 30(0) = 18000 x x y 0 600 900 0

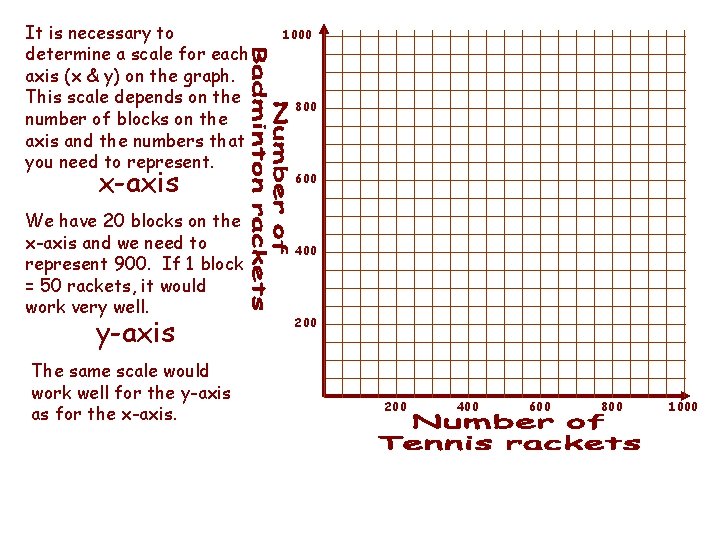
It is necessary to determine a scale for each axis (x & y) on the graph. This scale depends on the number of blocks on the axis and the numbers that you need to represent. x-axis We have 20 blocks on the x-axis and we need to represent 900. If 1 block = 50 rackets, it would work very well. y-axis The same scale would work well for the y-axis as for the x-axis. 1000 800 600 400 200 400 600 800 1000

x y 0 960 720 0 x y 0 600 900 0 1000 800 600 400 200 400 600 800 1000

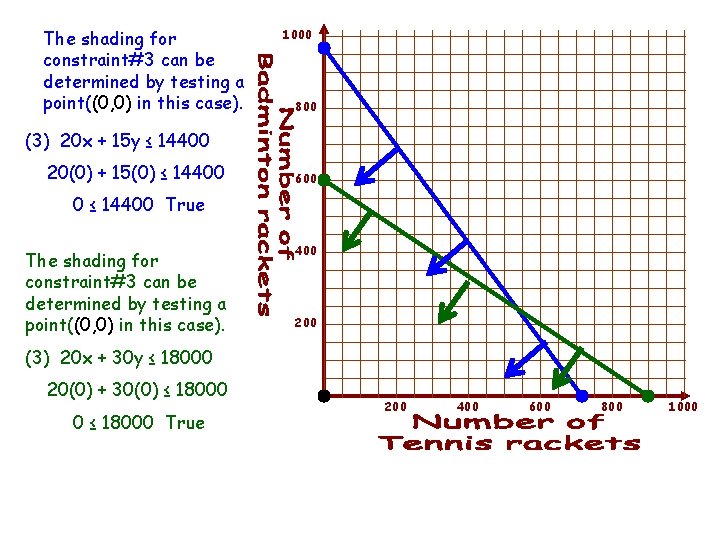
The shading for constraint#3 can be determined by testing a point((0, 0) in this case). 1000 800 (3) 20 x + 15 y ≤ 14400 20(0) + 15(0) ≤ 14400 600 0 ≤ 14400 True The shading for constraint#3 can be determined by testing a point((0, 0) in this case). 400 200 (3) 20 x + 30 y ≤ 18000 20(0) + 30(0) ≤ 18000 0 ≤ 18000 True 200 400 600 800 1000

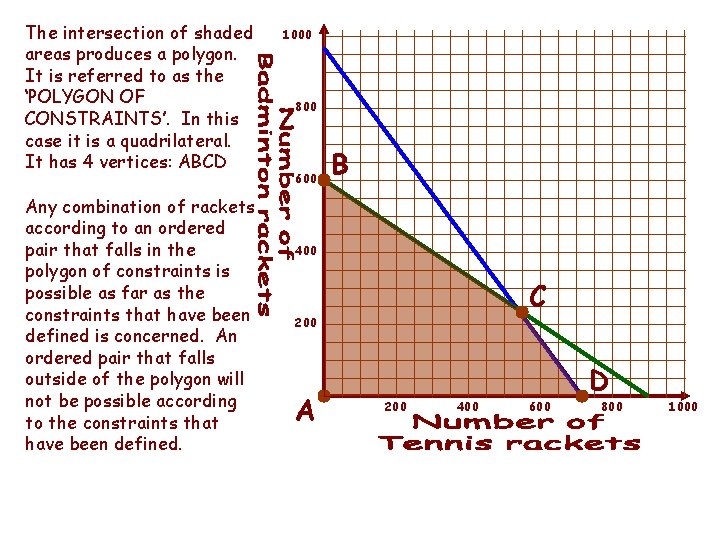
The intersection of shaded areas produces a polygon. It is referred to as the ‘POLYGON OF CONSTRAINTS’. In this case it is a quadrilateral. It has 4 vertices: ABCD Any combination of rackets according to an ordered pair that falls in the polygon of constraints is possible as far as the constraints that have been defined is concerned. An ordered pair that falls outside of the polygon will not be possible according to the constraints that have been defined. 1000 800 600 B 400 C 200 A 200 400 600 D 800 1000

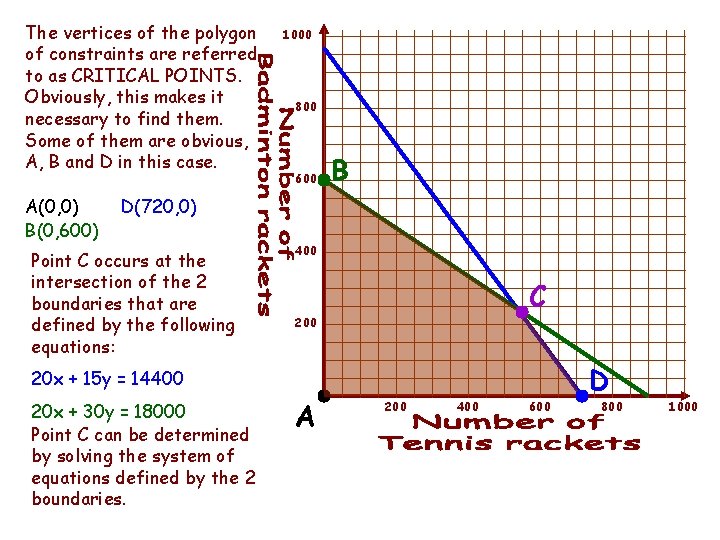
The vertices of the polygon of constraints are referred to as CRITICAL POINTS. Obviously, this makes it necessary to find them. Some of them are obvious, A, B and D in this case. A(0, 0) B(0, 600) 1000 800 600 B D(720, 0) Point C occurs at the intersection of the 2 boundaries that are defined by the following equations: 400 C 200 20 x + 15 y = 14400 20 x + 30 y = 18000 Point C can be determined by solving the system of equations defined by the 2 boundaries. A 200 400 600 D 800 1000

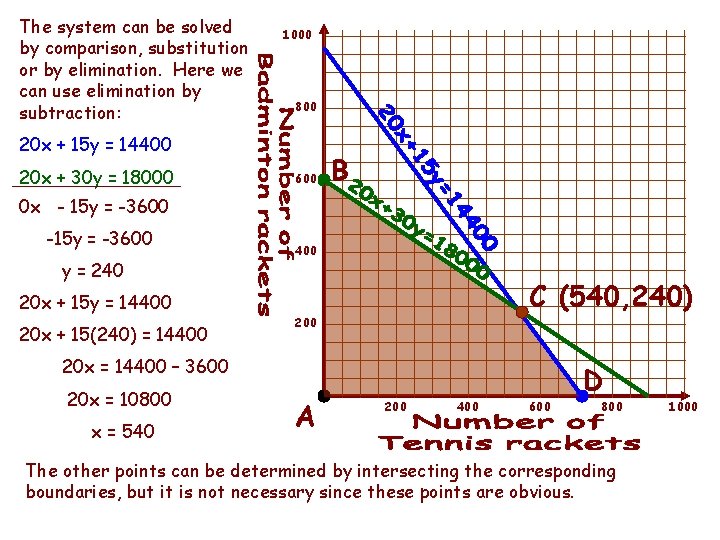
The system can be solved by comparison, substitution or by elimination. Here we can use elimination by subtraction: 1000 800 20 x + 15 y = 14400 20 x + 30 y = 18000 600 B 0 x - 15 y = -3600 -15 y = -3600 y = 240 20 x + 15 y = 14400 20 x + 15(240) = 14400 C (540, 240) 200 20 x = 14400 – 3600 20 x = 10800 x = 540 A 200 400 600 D 800 The other points can be determined by intersecting the corresponding boundaries, but it is not necessary since these points are obvious. 1000

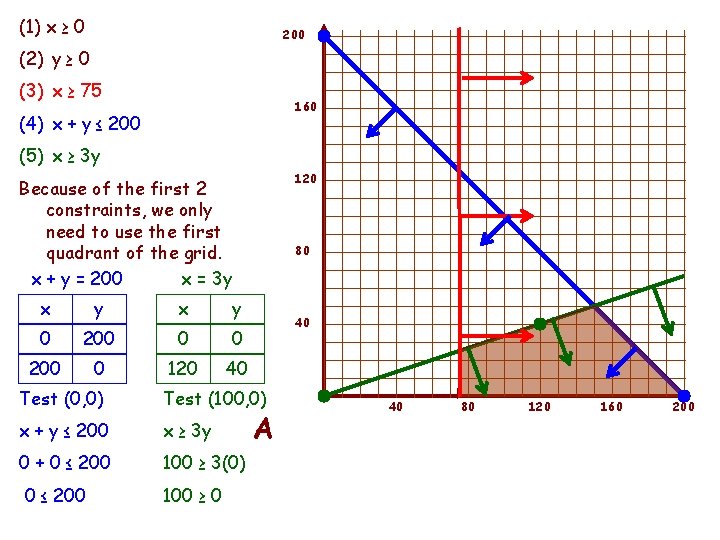
(1) x ≥ 0 200 (2) y ≥ 0 (3) x ≥ 75 160 (4) x + y ≤ 200 (5) x ≥ 3 y 120 Because of the first 2 constraints, we only need to use the first quadrant of the grid. x + y = 200 x = 3 y 80 x y 0 200 0 120 40 40 Test (0, 0) Test (100, 0) x + y ≤ 200 x ≥ 3 y 0 + 0 ≤ 200 100 ≥ 3(0) 0 ≤ 200 100 ≥ 0 A 40 80 120 160 200

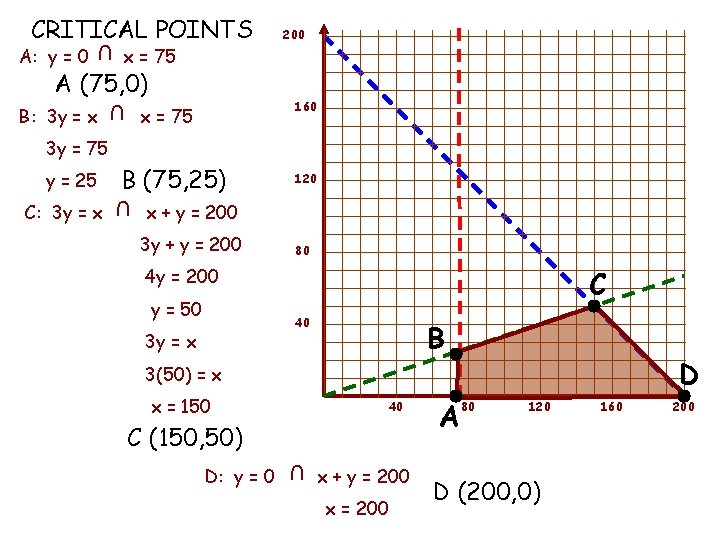
CRITICAL POINTS U A: y = 0 x = 75 A (75, 0) U B: 3 y = x 200 160 x = 75 3 y = 75 120 x + y = 200 3 y + y = 200 80 C 4 y = 200 y = 50 40 3 y = x B D 3(50) = x x = 150 40 C (150, 50) D: y = 0 U C: 3 y = x B (75, 25) U y = 25 x + y = 200 x = 200 A 80 120 D (200, 0) 160 200