Numeric Integration Methods Marq Singer Red Storm Entertainment

Numeric Integration Methods Marq Singer > Red Storm Entertainment > marqs@redstorm. com >

2 Talk Summary > Going to talk about: Euler’s method subject to errors > Implicit methods help, but complicated > Verlet methods help, but velocity inaccurate > Symplectic methods can be good for both >

3 Forces Encountered Dependant on position: springs, orbits > Dependant on velocity: drag, friction > Constant: gravity, thrust > > Will consider how methods handle these

4 Euler’s Method > Has problems > > Expects the derivative at the current point is a good estimate of the derivative on the interval Approximation can drift off the actual function – adds energy to system! Worse farther from known values Especially bad when: > > System oscillates (springs, orbits, pendulums) Time step gets large

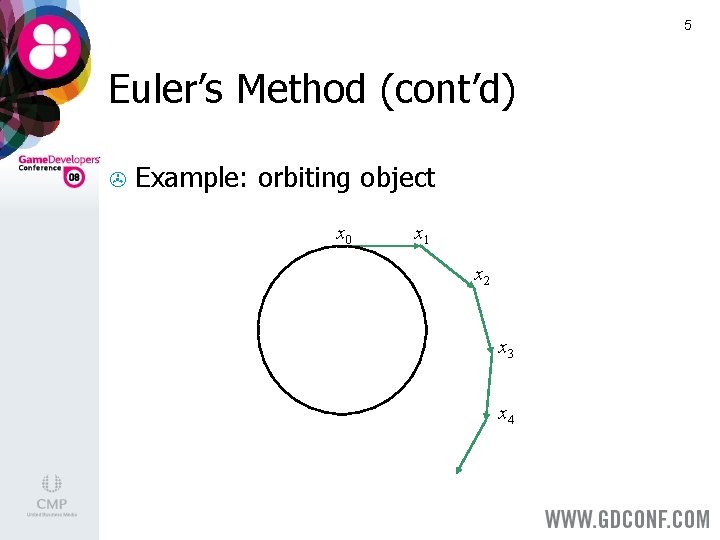
5 Euler’s Method (cont’d) > x Example: orbiting object x 0 x 1 x 2 x 3 x 4 t

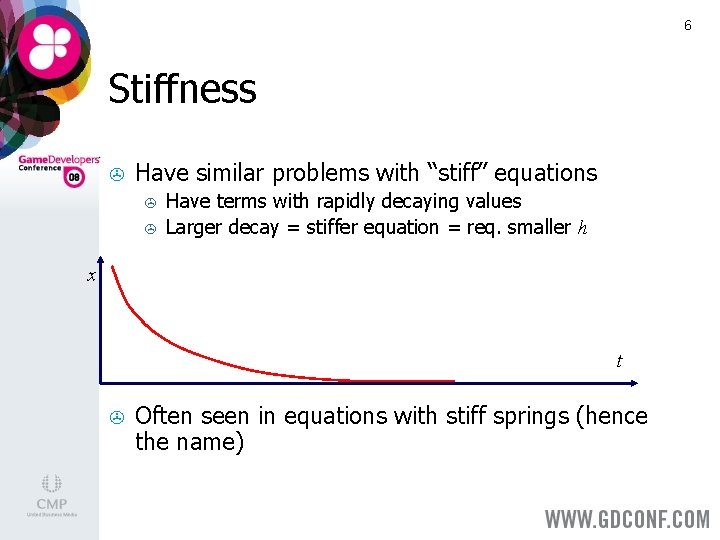
6 Stiffness > Have similar problems with “stiff” equations > > Have terms with rapidly decaying values Larger decay = stiffer equation = req. smaller h x t > Often seen in equations with stiff springs (hence the name)

7 Euler Lousy forces dependant on position > Okay forces dependant on velocity > Bad for constant forces >

8 Runge-Kutta Idea: single derivative bad estimate > Use weighted average of derivatives across interval > How error-resistant indicates order > Midpoint method Order Two > Usually use Runge-Kutta Order Four, or RK 4 >

9 Runge-Kutta (cont’d) RK 4 better fit, good for larger time steps > Tends to dampen energy > Expensive – requires many evaluations > If function is known and fixed (like in physical simulation) can reduce it to one big formula >

10 Runge-Kutta Okay forces dependant on position > Okay forces dependant on velocity > Great for constant forces > > But expensive: four evaluations of derivative

11 Implicit Methods Explicit Euler method adds energy > Implicit Euler dampens it > Use new velocity, not current > E. g. Backwards Euler: > > Better for stiff equations

12 Implicit Methods Result of backwards Euler > Solution converges - not great > But it doesn’t diverge! > x 0 x 1 x 3 x 2

13 Implicit Methods > How to compute or ? Derive from formula (most accurate) > Solve using linear system (slowest, but general) > Compute using explicit method and plug in value (predictor-corrector) >

14 Implicit Methods > Solving using linear system: > Resulting matrix is sparse, easy to invert

15 Implicit Methods > Example of predictor-corrector:

16 Backward Euler Okay forces dependant on position > Great forces dependant on velocity > Bad for constant forces > > But tends to converge: better but not ideal

17 Verlet Integration Velocity-less scheme > From molecular dynamics > Uses position from previous time step > Very stable, but velocity estimated > Good for particle systems, not rigid body >

18 Verlet Integration > Leapfrog Verlet > Velocity Verlet

19 Verlet Integration Better forces dependant on position > Okay forces dependant on velocity > Okay for constant forces > > Not too bad, but still have estimated velocity problem

20 Symplectic Euler Idea: velocity and position are not independent variables > Make use of relationship > Run Euler’s in reverse: compute velocity first, then position > Very stable >

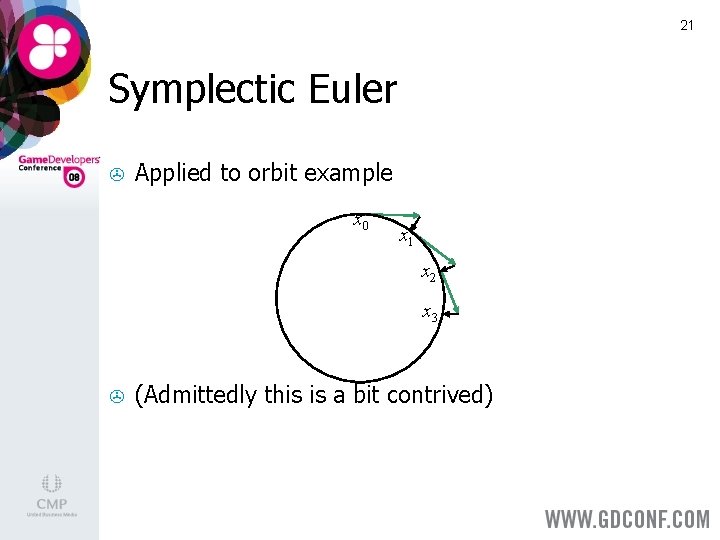
21 Symplectic Euler > Applied to orbit example x 0 x 1 x 2 x 3 > (Admittedly this is a bit contrived)

22 Symplectic Euler > Good forces dependant on position Okay forces dependant on velocity Bad for constant forces > But cheap and stable! > >

23 Which To Use? > > > With simple forces, standard Euler or higher order RK might be okay But constraints, springs, etc. require stability Recommendation: Symplectic Euler > > > Generally stable Simple to compute (just swap velocity and position terms) More complex integrators available if you need them -see references

24 References Burden, Richard L. and J. Douglas Faires, Numerical Analysis, PWS Publishing Company, Boston, MA, 1993. > Witken, Andrew, David Baraff, Michael Kass, SIGGRAPH Course Notes, Physically Based Modelling, SIGGRAPH 2002. > Eberly, David, Game Physics, Morgan Kaufmann, 2003. >

25 References Hairer, et al, “Geometric Numerical Integration Illustrated by the Störmer/Verlet method, ” Acta Numerica (2003), pp 1 -51. > Robert Bridson, Notes from CPSC 533 d: Animation Physics, University of BC. >