NPCompleteness Note Some illustrations are taken from KT

NP-Completeness Note. Some illustrations are taken from (KT) Kleinberg and Tardos. Algorithm Design (DPV) Dasgupta, Papadimitriou, and Vazirani. Algorithms

Decision problems Decision problem. • X is a set of strings. • Instance: string s. • Algorithm A solves problem X: A(s) = yes iff s X. Polynomial time. Algorithm A runs in poly-time if for every string s, A(s) terminates in at most p(|s|) "steps", where p( ) is some polynomial.

NP Def. Algorithm C(s, t) is a certifier for problem X if for every string s, s X iff there exists a string t such that C(s, t) = yes. NP. Decision problems for which there exists a poly-time certifier. Remark. NP stands for nondeterministic polynomial-time.

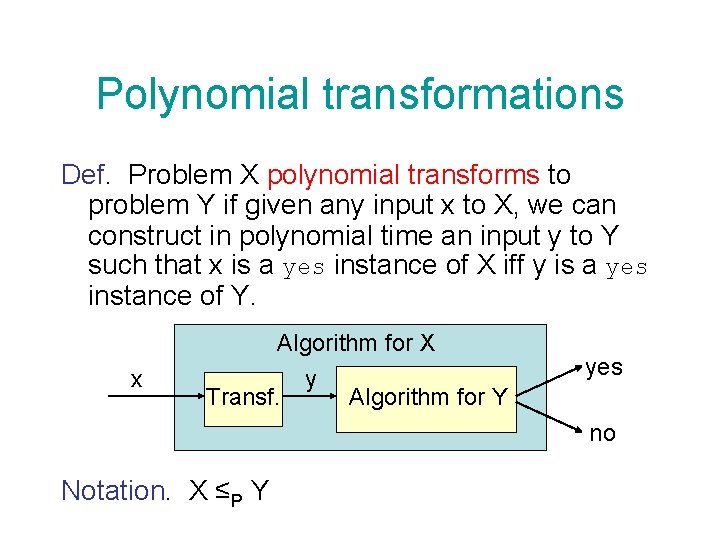
Polynomial transformations Def. Problem X polynomial transforms to problem Y if given any input x to X, we can construct in polynomial time an input y to Y such that x is a yes instance of X iff y is a yes instance of Y. x Algorithm for X y Transf. Algorithm for Y yes no Notation. X ≤P Y

NP-completeness Def. Problem Y is NP-complete if • Y is in NP and • for every problem X in NP, X P Y. Theorem. Suppose Y is an NP-complete problem. Then Y is solvable in polynomial time iff P = NP.

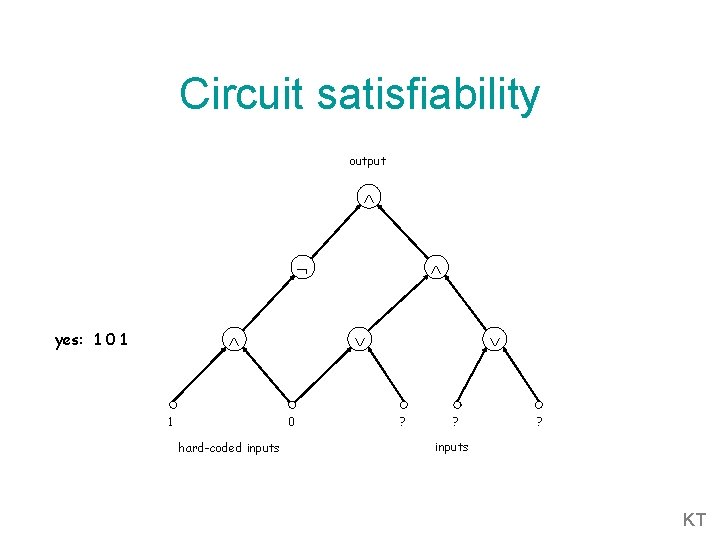
Circuit satisfiability output yes: 1 0 1 1 0 hard-coded inputs ? ? ? inputs KT

Proving NP-completeness Fact (Transitivity of p). If X P Y and Y P Z, then X P Z. Theorem. Problem Y is NP-complete if • Y is in NP and • There exists some NP-complete problem X such that X P Y. Proof. By def. of NP and transitivity of P.

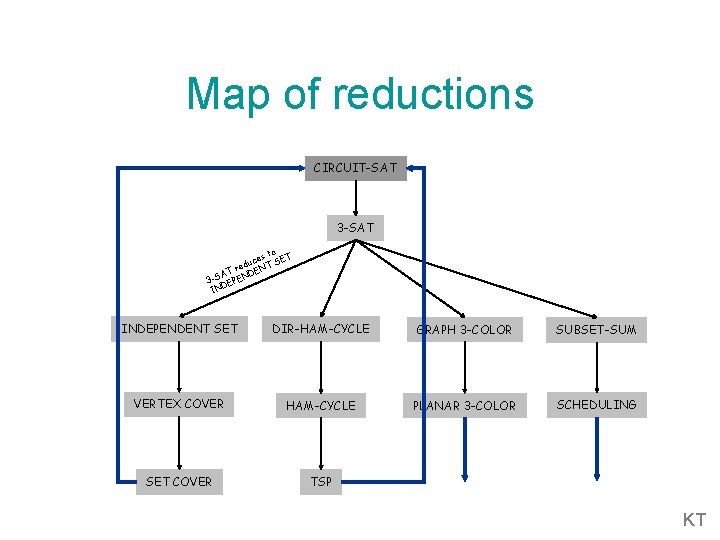
Map of reductions CIRCUIT-SAT 3 -SAT to es SET c u red NT AT ENDE S 3 P DE IN INDEPENDENT SET DIR-HAM-CYCLE GRAPH 3 -COLOR SUBSET-SUM VERTEX COVER HAM-CYCLE PLANAR 3 -COLOR SCHEDULING SET COVER TSP KT

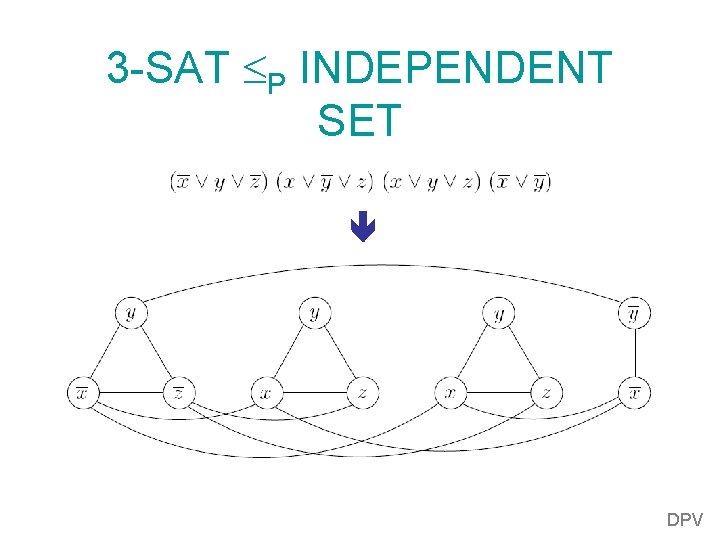
3 -SAT P INDEPENDENT SET DPV

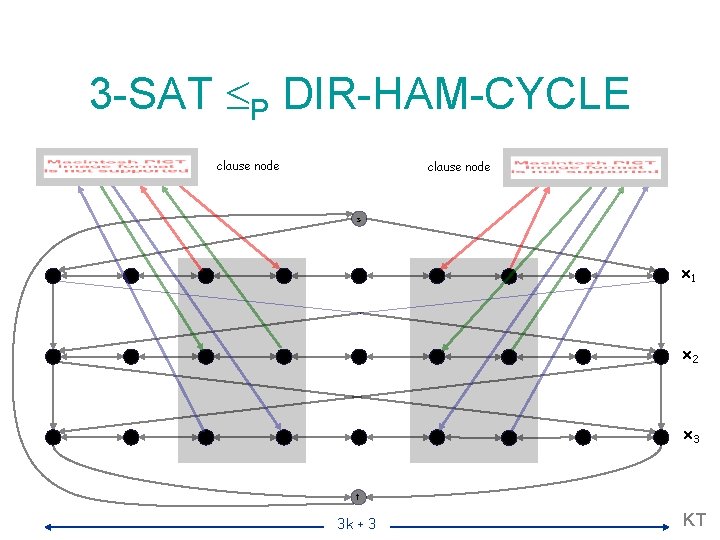
3 -SAT P DIR-HAM-CYCLE clause node s x 1 x 2 x 3 t 3 k + 3 KT

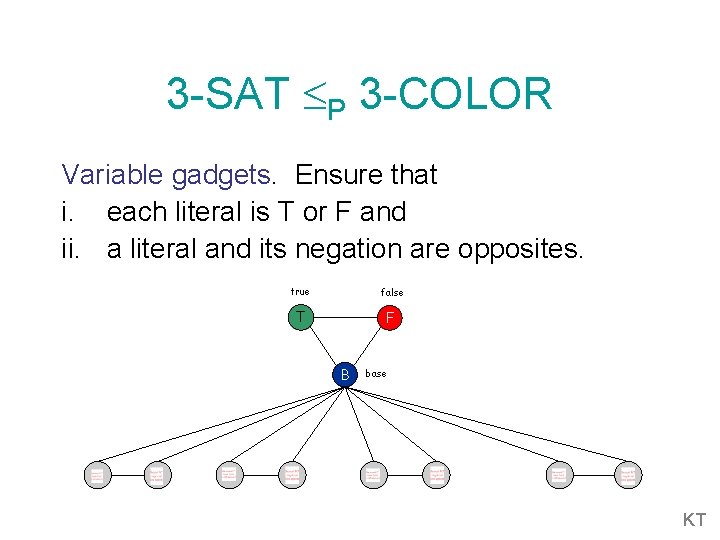
3 -SAT P 3 -COLOR Variable gadgets. Ensure that i. each literal is T or F and ii. a literal and its negation are opposites. true false T F B base KT

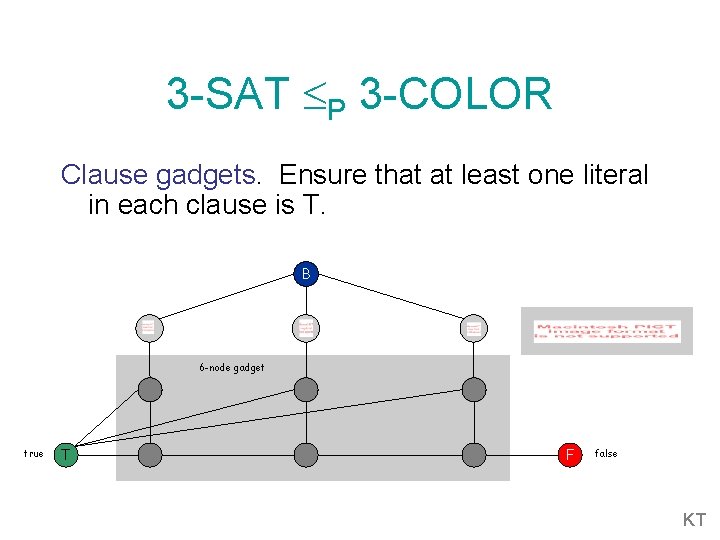
3 -SAT P 3 -COLOR Clause gadgets. Ensure that at least one literal in each clause is T. B 6 -node gadget true T F false KT

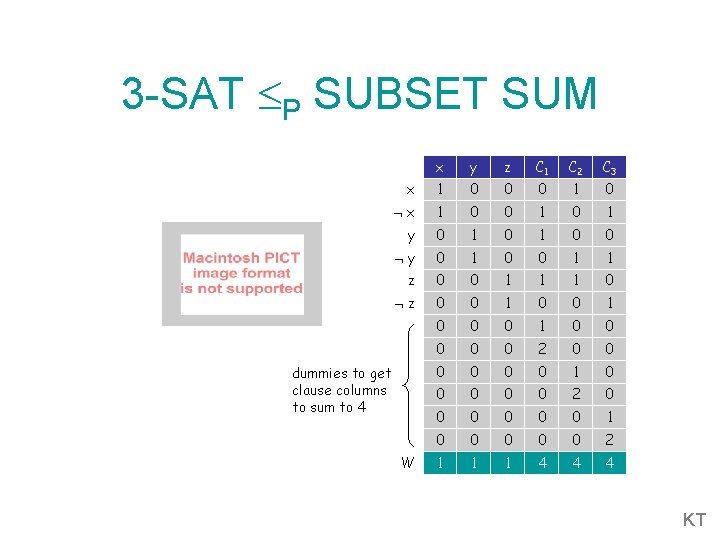
3 -SAT P SUBSET SUM x y z C 1 C 2 C 3 x 1 0 0 0 1 0 x 1 0 0 1 y 0 1 0 0 1 1 z 0 0 1 1 1 0 z 0 0 1 0 0 0 0 0 2 0 0 0 1 0 0 0 2 1 1 1 4 4 4 dummies to get clause columns to sum to 4 W KT

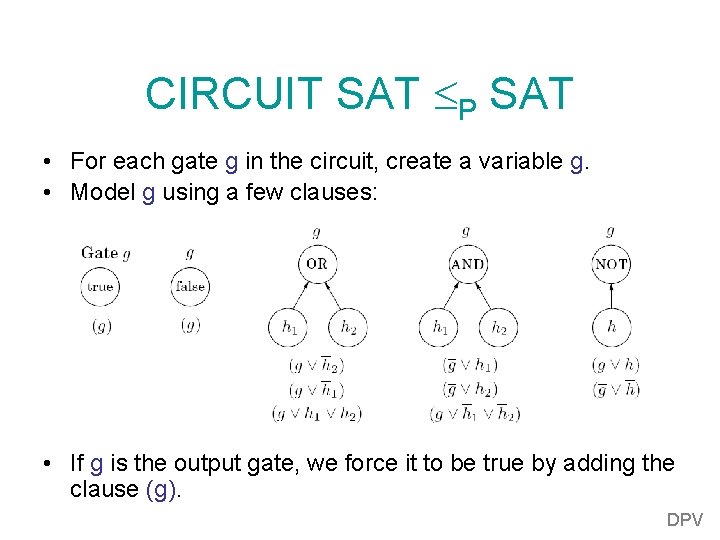
CIRCUIT SAT P SAT • For each gate g in the circuit, create a variable g. • Model g using a few clauses: • If g is the output gate, we force it to be true by adding the clause (g). DPV

A NP, A P CIRCUIT SAT Since A NP, there is an algorithm C(s, t) such that: • C checks, given an instance s and a proposed solution t, whether or not t is a solution of s. • C runs in polynomial time. In polynomial time, build a circuit D such that: • Known inputs of D are the bits of s. • Unknown inputs of D are the bits of t. • C’s answer is given at the output gate of D. • Size of D is polynomial in the number of inputs. • D‘s output is true if and only if t is a solution of s.

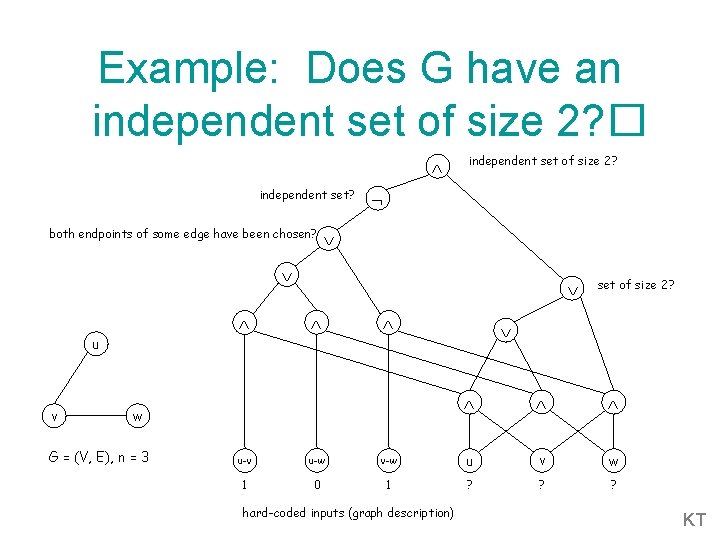
Example: Does G have an independent set of size 2? � independent set? both endpoints of some edge have been chosen? independent set of size 2? u v w G = (V, E), n = 3 set of size 2? u-v u-w v-w u v w 1 0 1 ? ? ? hard-coded inputs (graph description) KT