Nielsen and Chuang Chap 4 Quantum Circuits p

Nielsen and Chuang Chap 4 Quantum Circuits: p 171 -215 Dr. Charles Tappert The information presented here, although greatly condensed, comes almost entirely from the course textbook: Quantum Computation and Quantum Information by Nielsen & Chuang

4 Quantum Circuits n This chapter develops the fundamental principles of quantum computation n n Establishes the building blocks for quantum circuits, a universal language for describing sophisticated quantum computations The next two chapters cover the two known-todate fundamental quantum algorithms n n Quantum Fourier transform Quantum search algorithm

4 Quantum Circuits n This chapter introduces two main ideas n Quantum circuit model n n Universal sets of gates n n The fundamental model of quantum computation That can express any quantum computation This chapter is the most reader-intensive of all the chapters, with high density of exercises n Facility with the quantum circuit model is easy but requires grasping a large number of simple results and techniques

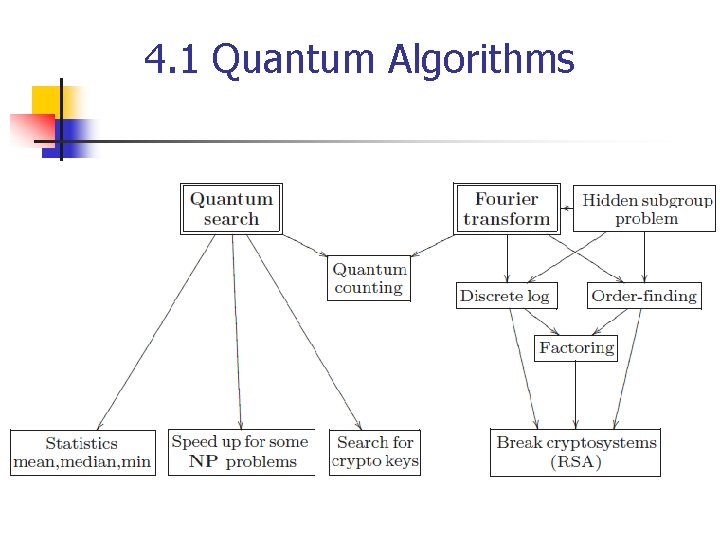
4. 1 Quantum Algorithms n n The spectacular promise of quantum computers is to enable new algorithms, which allows solving problems efficiently that require huge resources on a classical computer Figure 4. 1. The main quantum algorithms and their relationships and notable applications n Note quantum counting algorithm, a combination of quantum Fourier transform and search algorithms

4. 1 Quantum Algorithms

4. 2 Single Qubit Operations Common Single Qubit Gates

4. 2 Single Qubit Operations n n The single qubit state can be visualized as a point on the unit sphere called the Bloch sphere representation And the Bloch vector is

4. 2 Single Qubit Operations Exercise 2. 11 required by Exercise 4. 1

4. 2 Single Qubit Operations Exercise 4. 1

4. 2 Single Qubit Operations n Rotation operators for the Pauli matrices

4. 2 Single Qubit Operations Exercise 4. 2

4. 2 Single Qubit Operations Exercise 4. 7

4. 2 Single Qubit Operations n n An arbitrary unitary operator on a single qubit can be written in many ways as a combination of rotations and global phase shifts Theorem 4. 1: (Z-Y decomposition for a single qubit) Suppose U is a unitary operation on a single qubit. Then there exist real numbers n proof in textbook

4. 2 Single Qubit Operations n n The utility of Theorem 4. 1 is in the corollary Corollary 4. 2: Suppose U is a unitary gate on a single qubit. Then there exist unitary operators A, B, C on a single qubit such that

4. 2 Single Qubit Operations Exercise 4. 13

4. 2 Single Qubit Operations Common Single Qubit Gates

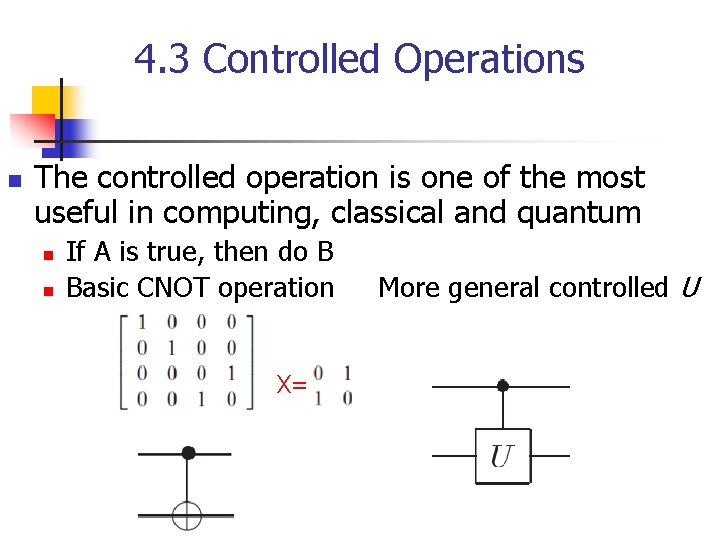
4. 3 Controlled Operations n The controlled operation is one of the most useful in computing, classical and quantum n n If A is true, then do B Basic CNOT operation X= More general controlled U

4. 3 Controlled Operations n More CNOT gate information from the book Approaching Quantum Computing click here n Computes CNOT information n n Using ket/bra and matrix/vector formulations In particular, computes CNOT matrix as the sum of the outer products of the input and output basis bra/ket vectors

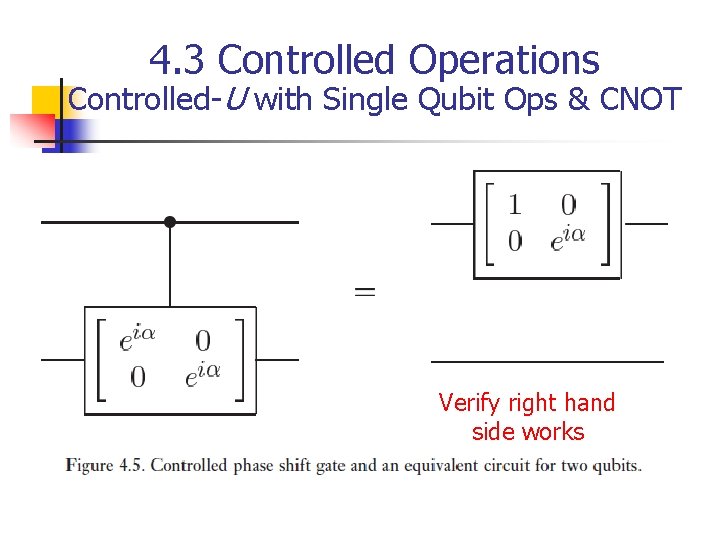
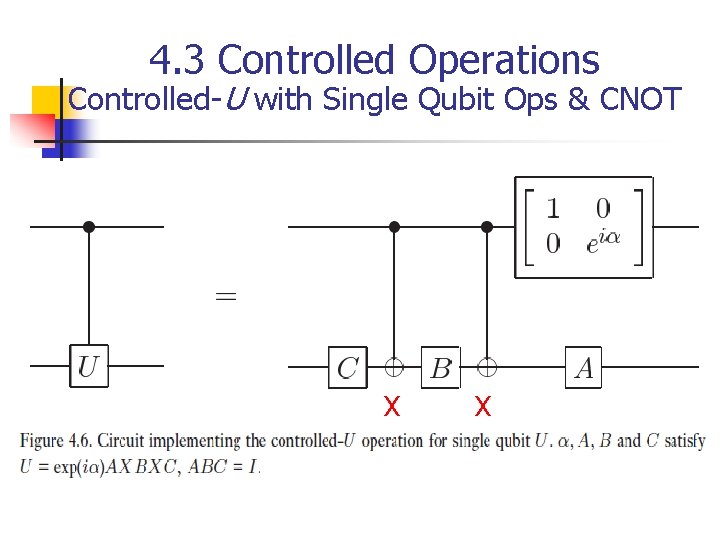
4. 3 Controlled Operations Controlled-U with Single Qubit Ops & CNOT n n Understand how to implement controlled-U operation for arbitrary single qubit U using only single qubit operations and the CNOT gate Step one of two-part procedure n n Apply phase shift exp(ia) on the target qubit controlled by the control qubit That is

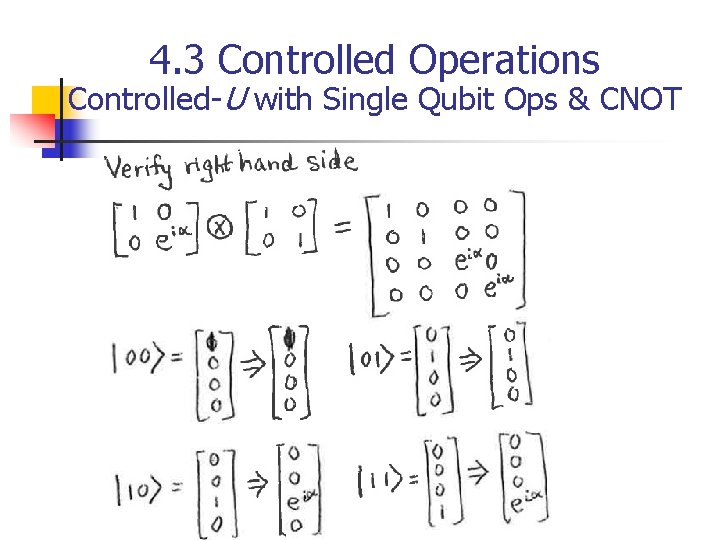
4. 3 Controlled Operations Controlled-U with Single Qubit Ops & CNOT Verify right hand side works

4. 3 Controlled Operations Controlled-U with Single Qubit Ops & CNOT

4. 3 Controlled Operations Controlled-U with Single Qubit Ops & CNOT n Step two of two-part procedure – figure 4. 6 n n n From Corollary 4. 2, let where A, B, and C are single qubit ops and ABC = I If the control qubit is set, then is applied to the second qubit, otherwise the operation ABC = I is applied yielding no change Thus, the right hand side works and it contains only CNOT and single qubit operations

4. 3 Controlled Operations Controlled-U with Single Qubit Ops & CNOT X X

4. 4 Measurement n To denote a projective measurement in the computational basis, we use the meter symbol

4. 4 Measurement n There are two important principles about quantum circuits worth emphasis n Principle of deferred measurement: measurements can always be moved to the end of the circuit n n If measurement results are used in the circuit, classically controlled operations can be replaced by quantum controlled operations Principle of implicit measurement: quantum wires not measured at the end of the circuit can be assumed to be measured n Obvious but surprisingly useful result

4. 5 Universal Quantum Gates n Universal classical computation gates exist n n Because the Toffoli gate is universal for classical computation, quantum circuits subsume classical circuits Similarly, there exist sets of gates universal for quantum computation

4. 5. 1 Two-level Unitary Gates are Universal n An arbitrary unitary matrix U can be decomposed into a product of two-level unitary matrices n n Matrices acting non-trivially on two-or-fewer vector components Proof in textbook

4. 5. 2 Single Qubit and CNOT Gates are Universal n n n The previous section showed that an arbitrary unitary matrix U can be decomposed into a product of two-level unitary matrices We now show that single qubit and CNOT gates together can implement an arbitrary two-level unitary operation on the state space of n qubits Therefore, single qubit and CNOT gates are universal

4. 5. 3 A Discrete Set of Universal Operations n The previous section showed that single qubit and CNOT gates are universal n n But no method is known to implement these gates so they are resistant to errors We now find a universal set of gates that chapter 10 will show perform in error-resistant fashion using quantum error-correcting codes

4. 5. 4 Approximating Arbitrary Unitary Gates is Generally Hard n n We have seen that any arbitrary transformation on n qubits can be built from a small set of elementary gates However, this it is often not possible to do this efficiently n Most can only be implemented very inefficiently

4. 6 Summary of the Quantum Circuit Model of Computation n n In this book the term quantum computer = quantum circuit model of computation Summary of key elements of the model n n n Classical resources: classical + quantum parts A suitable state space: 2 n-dimensional Hilbert space Ability to prepare states in the computational basis Ability to perform quantum gates Ability to perform measurements in the computational basis