Multicoloring bounded tree width graphs and planar graphs

Multicoloring bounded tree width graphs and planar graphs Guy Kortsarz, Rutgers University, Camden Joint work with M. M Halldorsson.

Scheduling dependent jobs Jobs compete on resources Create a graph. Each job is a vertex. Two vertices are adjacent if dependent Two possibilities: Single unit jobs Jobs that require more than one unit of processing Two conflicting jobs can not be executed at the same time unit
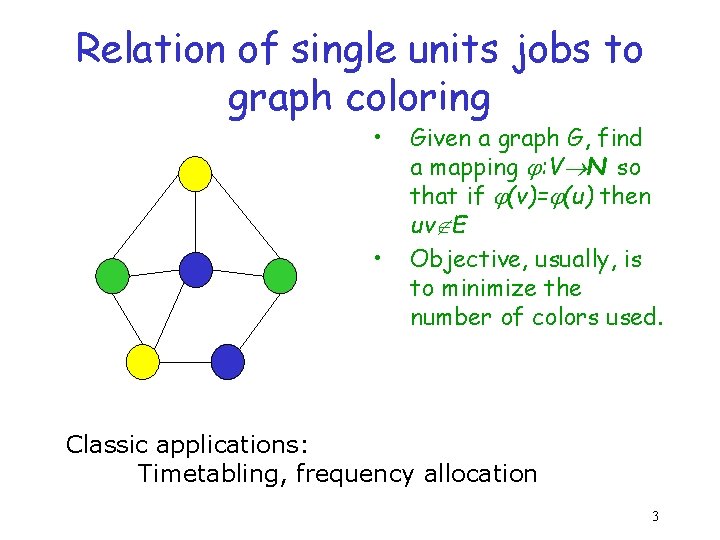
Relation of single units jobs to graph coloring • • Given a graph G, find a mapping : V N so that if (v)= (u) then uv E Objective, usually, is to minimize the number of colors used. Classic applications: Timetabling, frequency allocation 3
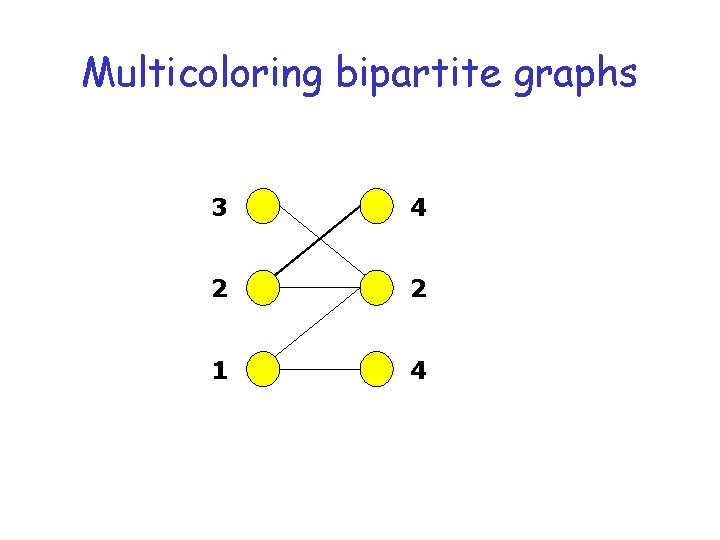
Multicoloring bipartite graphs 3 4 2 2 1 4
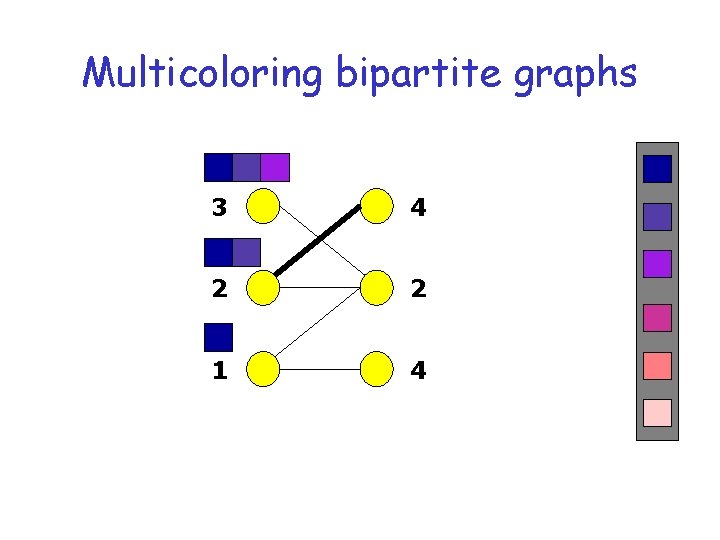
Multicoloring bipartite graphs 3 4 2 2 1 4

Formal definition of the multicoloring problem • Input: Graph G=(V, E), with lengths x(v) on the vertices • Output: An assignment : V 2 N such that adjacent vertices do not receive overlapping times. (v) (u) implies that uv E • Goal: minimize the maximum integer: • Minimize Maxu V { f (u) } • f (u)- The largest color of u.

Multicoloring is often easy 6 -clique More generally, chordal graphs, even perfect, are no harder to multicolor than to color. Maybe one reason why multicolorings are not more common. 7

Some other objectives than makespan (= number of colors) • • Sum of completion times of jobs – For each vertex, count the last time unit assigned, and sum these values up Weighted sum of completion times – Vertices additionally have importance value attached Total lateness – Assumes deadline for each task Sum of flow times – Assumes release time of each job

“Sum of completion times” in Graph coloring? • • Recall we color with numbers, : V N Sum of a coloring = Sum of the values assigned to the vertices Sum coloring problem: – Find a coloring that minimizes the chromatic sum, This measure is more favorable to the users (as a whole), while the makespan is desired by the system (machines) 9

The Sum Multicoloring problem Ø Each vertex v V requires x(v) 1 distinct colors. Ø A proper coloring of G is a function Ψ: V → 2 N, such that adjacent vertices are assigned distinct sets of numbers (colors). Let fΨ(v) denote the maximum color assigned to v by Ψ. Ø The sum multicoloring (SMC) problem: find a multicoloring Ψ that minimizes v V fΨ(v). • The preemptive model (p. SMC): each vertex can get any set of colors. • The no-preemption model (np. SMC): assign to each vertex a contiguous set of colors. 10
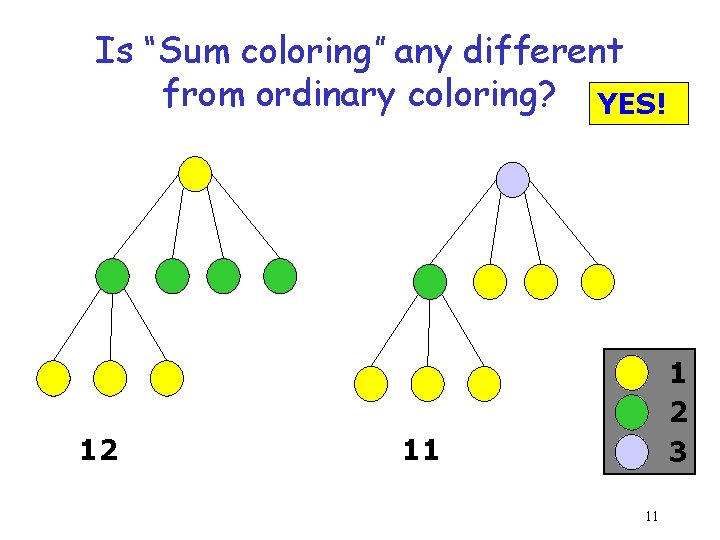
Is “Sum coloring” any different from ordinary coloring? YES! 12 1 2 3 11 11
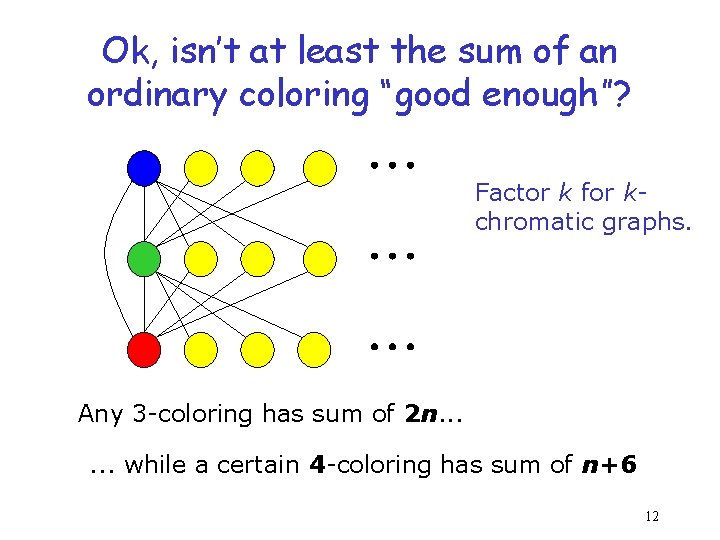
Ok, isn’t at least the sum of an ordinary coloring “good enough”? Factor k for kchromatic graphs. Any 3 -coloring has sum of 2 n. . . while a certain 4 -coloring has sum of n+6 12

Multicoloring p max demand bounded tree width graphs • Sum multicoloring non preemptively of trees is in P. [Halldórsson, K, Proskurowski, Salman, Shachnai and Telle] • Preemptive sum multicoloring of Paths is in P. An ICALP paper (!) [Kovács] • Preemptive coloring of trees is NPC (!) [Marx] • See the collection of papers maintained by Daniel Marx for more results: http: //www 2. informatik. huberlin. de/~dmarx/sum. php

An (important? ) breakpoint lemma Consider the collection of breakpoints r, r+1, …. . , s There exists r j s so that: |{ ai | ai j µ }| n/(j ln(s/r)) Probably not written in any place that you can find, but known.

Breakpoint Lemma • For any q, there is a sequence of breakpoints bi satisfying such that the total breakpoint overhead is at most b 1 b 2 b 3 b 4 15

np-MC bounded tree width graphs • This can be solved by DP in what I call the standard way. Running time O(n · (kp log n)k+1) • Two difficulties: bad time for large p • Also, we need a sum that uses few colors • This is because we are going to color the classes in the breakpoint lemma one after the other. • How much they wait depends on the makespann not the sum.

Sum coloring with few colors BTW graphs • Ignore all bits but roughly log n for every x(v) • This means that the numbers can be divided by a large number q. • Dividing by q we get an instance with small ratio p/pmin • Can use the previous solution and duplications and get only 1+ penalty and get roughly (n/ )k running time.

Application for np-SMC planar graphs • • It is shown that np-SMC planar graphs admits a PTAS in time roughly (log n)d *n with d =p/pmin We make d=log n/loglog n by methods discussed. • Baker decomposition into k 2 -outerplanar G 1 and outerplanar and small GO. • Biased round robin: color mainly G 1. Color GO only after k rounds of coloring G 1. • This is OK as GO is negligible. • We can assume d is small due to the breakpoint lemma.

The color sum • G 1 has size at most n/k 2 (one of the choices). We also get very small d. • Solve optimally by dp, but truncate the coloring after (1/ )b/a colors. Cost ≤ OPT. And poly time due to value of d. • Finish by 4 -coloring remaining vertices • The color starts with (1/ )b/a Cost of O(n/k 2)* (1/ )b/a ≤ n when k >> -2 (b/a).

Preemptive multicoloring of graphs • A general tool for O(1) makspan coloring: preemptive scaling. We are able to reduce job lengths to log n paying only (1+ ), even if start with p exponential. • Claim 1: Say that all x(v) are divisible by q. Then then if x(v)/q c ln n for every v then: (I) q (I/q) (1+ ) (I) • Was not a problem in non-pree’. Here use random proof and its non trivial.

Reduce to log n • Split jobs to (roughly) log n most significant bits and the rest • The large parts of numbers are all divisible by some large q • Reduce these numbers to log n bits (small loss). The O(log n) is derived • Color first by round robin the small part of the numbers non-preemptively • Small delay because constant colors and small numbers • Then take the solution to the O(log n) instance • The coloring for x’/q is repeated q times. Uses the randomized proof.

My most surprising claim ever • Say you want to preemptively multicolor a BTW graph • There is a family of colorings so that for every instance there exists a coloring in the family that approximates the SMC by (1+ ) factor • The key property: the number of different colorings of v in the family is polynomial in n • This allows finding the best solution via DP if treewidth constant • The existence is proven by modifying OPT

What is the surprise? • The colorings in our family depend only on a specific k-coloring of the graph, on n and on p • In particular, it does not depend on the actual connections in the graph, nor on the distribution of color requirements • Hence the name universal

The universal family • Split the colors of every vertex in powers of (1+ ) • Segment i: colors (1+ )i to (1+ )i+1 • In every segment, treat the coloring as a makespann instance • Thus in every segment O(log n) colors • Make the number of segments in which a vertex is colored, constant

How to bound # of segments • For every vertex v, its colors that are smaller than x(v) or larger than (2/ )x(v) are removed from OPT • Instead they are replace by round robins that are performed every (roughly) 1/ rounds • The key: the number of “non-standard” segments for every v is O(log 1+ ( 2 ) )

The number of preemption for v In every segment v has O(log n) preemptions • # colors per segment clog n. Choose c’ log n of them for v • The number of possibilities for v is O((2 clog n) f( ) ) hence polynomial in n • The round robin, executed only every 1/ rounds and adds O( opt)

Open problems • What can we say about np-MC of planar graphs? • Of course 4/3 lower bound. • I have no idea how to do 4/3. • But giving 2 ratio is easy. • A planar graph can be decomposed into two bipartite graphs. • Optimally color first the one with smallest p. Then the other. Ratio 2. 4/3 anyone?

Quotes on knowledge. Fiery the angels fell. Deep thunder rolled around their shoulders. . . burning with the fires of Orc. Blade Runner & Paradise Lost. • I've seen things you people wouldn't believe. Attack ships on fire off the shoulder of Orion. I watched c-beams glitter in the dark near Tannhäuser Gate. All those moments will be lost in time, like tears in rain. Time to die. Blade Runner

What did I not know in 1999? • De-vos et al. 2004; Demaine, Hajiaghayi, Kawarabayashi 2005 • H-minor-free graphs can have their vertices partitioned into k pieces such that deleting any one piece results in bounded treewidth. • Paradise lost: if I knew then, I would write the paper for H-minor free graphs. Also bounded genus graphs, etc.
- Slides: 29