Planar Graphs Graph G is planar if it













![Steinitz Theorem • Theorem [Steinitz]. A simple graph G is planar and 3 -connected Steinitz Theorem • Theorem [Steinitz]. A simple graph G is planar and 3 -connected](https://slidetodoc.com/presentation_image_h/1c33ea620643220e54fda3e94500e542/image-19.jpg)




![Tutte’s Embedding • Theorem [Tutte]. Let C be a peripheral cycle of length d Tutte’s Embedding • Theorem [Tutte]. Let C be a peripheral cycle of length d](https://slidetodoc.com/presentation_image_h/1c33ea620643220e54fda3e94500e542/image-25.jpg)



- Slides: 30

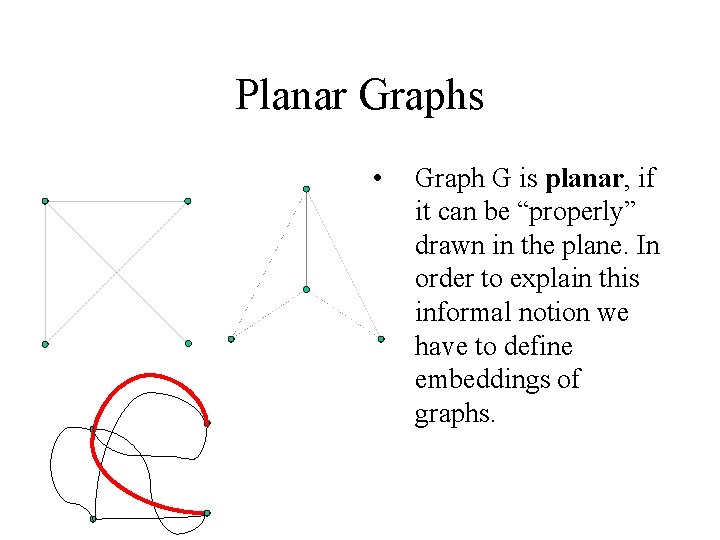
Planar Graphs • Graph G is planar, if it can be “properly” drawn in the plane. In order to explain this informal notion we have to define embeddings of graphs.

Embeddings • • • Let S be a “nice” topological space such as metric space. An embedding of a general graph : G S is defined as follows: 1. Injective mapping : V(G) S 2. Family of continuous mappings e: [0, 1] S, for each edge e = uv so that e( 0) = (u) and e(1) = (v). 3. In the interior of the interval e is injective and 4. its image contains no point that is an image of some other vertex or edge. Connected component of S – (G) is called a face of the embedding. Graph G is planar, if it can be embedded in the plane.

Exercises • N 1. Show that K 4 can be embedded in the plane. • N 2. Show that Petersen graph can be embedded in the projective plane. • N 3. Prove: graph is planar if and only if it can be embedded in a sphere. (Hint: use stereographic projection. )

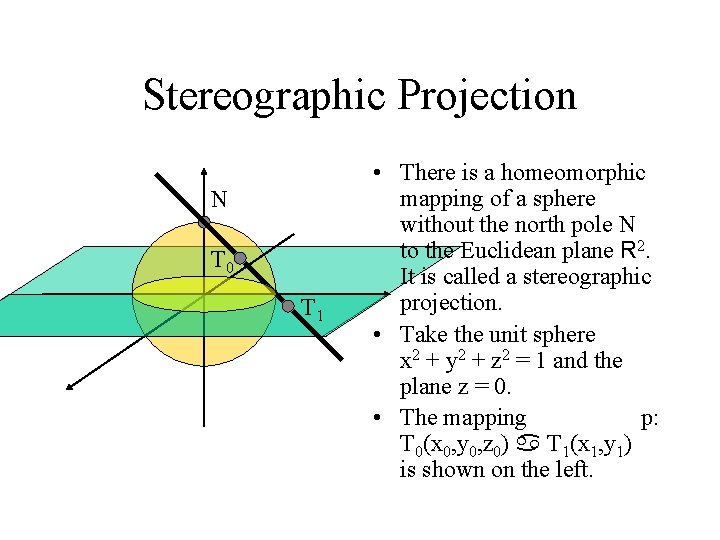
Stereographic Projection N T 0 T 1 • There is a homeomorphic mapping of a sphere without the north pole N to the Euclidean plane R 2. It is called a stereographic projection. • Take the unit sphere x 2 + y 2 + z 2 = 1 and the plane z = 0. • The mapping p: T 0(x 0, y 0, z 0) a T 1(x 1, y 1) is shown on the left.

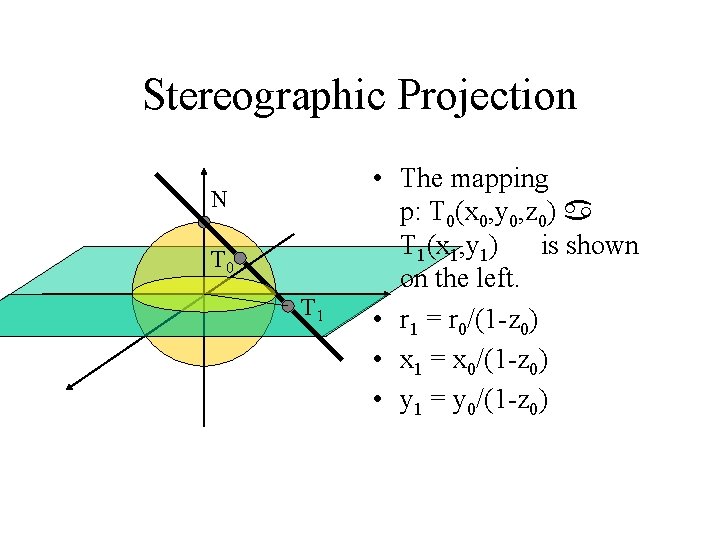
Stereographic Projection N T 0 T 1 • The mapping p: T 0(x 0, y 0, z 0) a T 1(x 1, y 1) is shown on the left. • r 1 = r 0/(1 -z 0) • x 1 = x 0/(1 -z 0) • y 1 = y 0/(1 -z 0)

Example • Take the Dodecahedron and a random point N on a sphere. • Stereographic projection is depicted below.

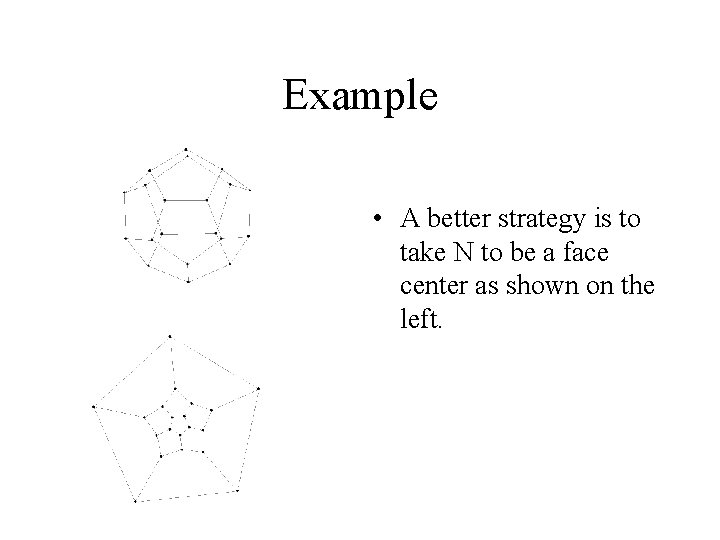
Example • A better strategy is to take N to be a face center as shown on the left.

Euler formula for planar graphs • For a connected plane graph G with v vertices, e edges and f faces we have: • v – e + f = 2. • Warning: the outer face is counted!

Fary’s Theorem • Each simple planar graph admits a specially nice embedding. • Theorem (Fary): Each simple planar graph can be embedded in the plane in such a way that all edges are represented with straight line segments.

Kuratowski’s Theorem • Theorem (Kuratowski): Graph G is planar if and only if it contains no subdivision of K 5 neither a subdivision of K 3, 3. • Graphs K 5 and K 3, 3 are called the Kuratowski graphs.

Applications of Kuratowski’s Theorem • Any graph can now be either drawn in the plane or one can find a subdivision of a Kuratowski graph in it. • For any graph on n vertices there are efficient algorithms for checking if the graph is planar. The best one runs in linear time ( O(n)).

Wagner Theorem • Similar to Kuratowski: • Theorem (Wagner): Graph G is planar if and only if it contains no subgraph that can be contracted to one of the two Kuratowski subgraphs.

Exercises • N 4. By using Kuratowski’s Theorem show that the Petersen graph is non-planar. • N 5. By using Wagner’s Theorem show that the Petersen graph is non-planar. • N 6. Show thst far any planar graph with v vertices, e edges and girth g the following is true: (g-2)e g(v-2) • N 7. By using Euler’s formula show that the Petersen graph is non. -planar.

Skeleta of Geometric Bodies • To each geometric polyhedron T we may associate a graph G(T), by selecting the vertices and edges of the polyhedron. The obtained graph is called the skeleton of T. • Sometimes we use the same name for the polyhedron and for the graph. Later we will see why such a naiming is permitted.

Melancholia I • The renowned graphics “Melancholia I” by Albrecht Dürer contains a misterious body (polyhedron) whose construction is now understood.

Dürer Polyhedron • It is obtained from an elongated cube by truncating the top and bottom vertex. • A polyhedron with 8 faces is obtained: – 6 pentagons – 2 regular triangles

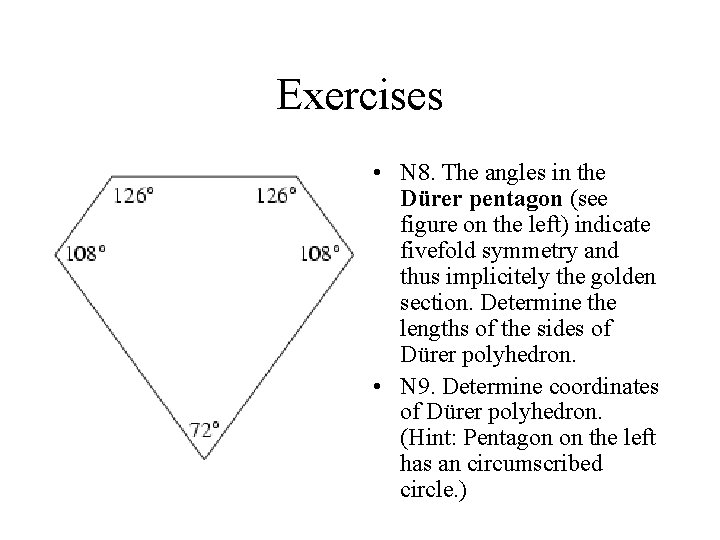
Exercises • N 8. The angles in the Dürer pentagon (see figure on the left) indicate fivefold symmetry and thus implicitely the golden section. Determine the lengths of the sides of Dürer polyhedron. • N 9. Determine coordinates of Dürer polyhedron. (Hint: Pentagon on the left has an circumscribed circle. )

Skeleta of Polyhedra are Modeled by Graphs • On the left we se Dürer graph, with 12 vertices and 18 edges, the skeleton of Dürer polyhedron. Graph is isomorphic to the generalized Petersen graph G(6, 2).
![Steinitz Theorem Theorem Steinitz A simple graph G is planar and 3 connected Steinitz Theorem • Theorem [Steinitz]. A simple graph G is planar and 3 -connected](https://slidetodoc.com/presentation_image_h/1c33ea620643220e54fda3e94500e542/image-19.jpg)
Steinitz Theorem • Theorem [Steinitz]. A simple graph G is planar and 3 -connected if and only if it is the skeleton of a convex three-dimensional polyhedron.

Fullerene • Fullerene is a convex trivalent polyhedron, whose faces are only pentagons and hexagons.

Dodecahedron • Dodecahedron is the smallest fullerene.

Buckminster Fullerene • The most well-known fullerene is Buckminster fullerene on 60 vertices. It is a truncated icosahedron. • Buckminster fullerene is a model of a carbon molecule.

Exercises • N 10. Each fullerne has exactly 12 pentagonal faces. • N 11. Each fullerene has an even number of vertices. • N 12. A Fullerene has at least 20 vertices. • N 13. For each even n, n ¸ 20, n ¹ 22 there exists a fullerne on n vertices.

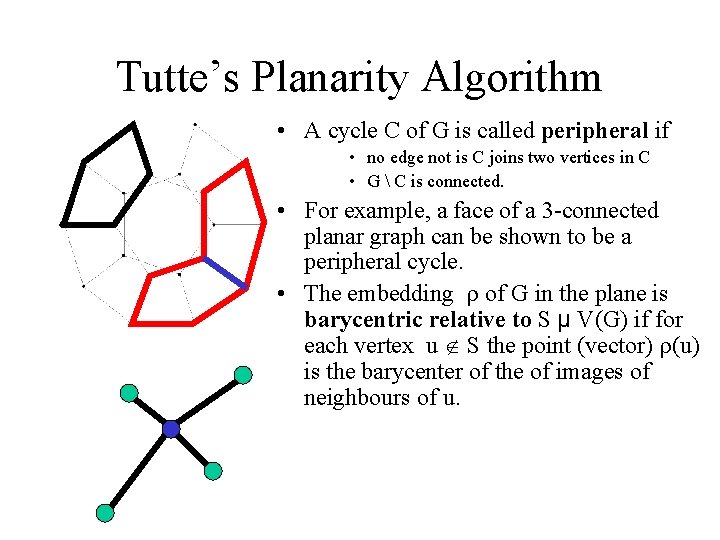
Tutte’s Planarity Algorithm • A cycle C of G is called peripheral if • no edge not is C joins two vertices in C • G C is connected. • For example, a face of a 3 -connected planar graph can be shown to be a peripheral cycle. • The embedding r of G in the plane is barycentric relative to S µ V(G) if for each vertex u Ï S the point (vector) r(u) is the barycenter of the of images of neighbours of u.
![Tuttes Embedding Theorem Tutte Let C be a peripheral cycle of length d Tutte’s Embedding • Theorem [Tutte]. Let C be a peripheral cycle of length d](https://slidetodoc.com/presentation_image_h/1c33ea620643220e54fda3e94500e542/image-25.jpg)
Tutte’s Embedding • Theorem [Tutte]. Let C be a peripheral cycle of length d in a connected simple graph G. Let s be a mapping from V(C) to the vertices of a convex d-gon in R 2 such that adjacent vertices in C are adjacent in the polygon. The unique barycentric representation determines a drawing of G in R 2. This drawing has no crossings if and only if the graph is planar. • [The vertex coordinates in R 2 can be obtained by solving a linear system. This gives an O(n 3) planarity test algorithm].

Prisms • Skeleton of an n-sided prism is denoted by Pn. Graph is planar, trivalent and has 2 n vertices.

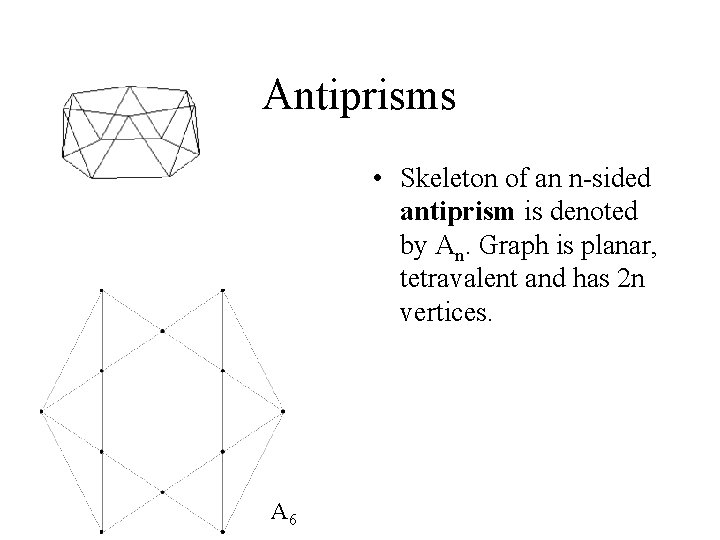
Antiprisms • Skeleton of an n-sided antiprism is denoted by An. Graph is planar, tetravalent and has 2 n vertices. A 6

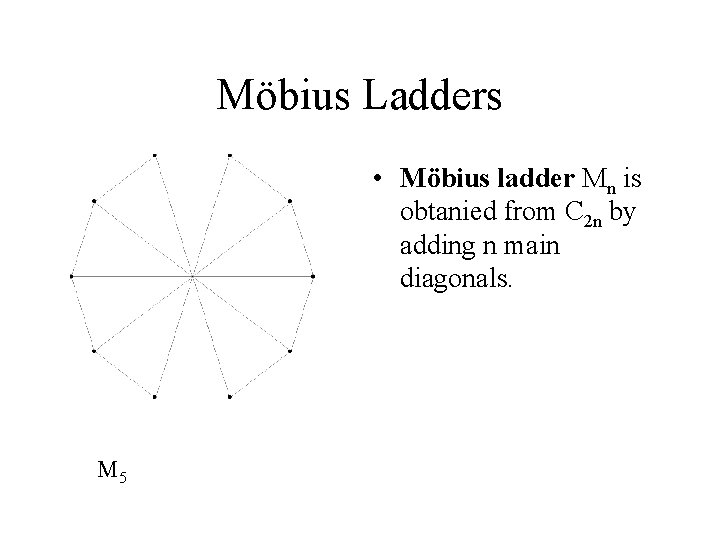
Möbius Ladders • Möbius ladder Mn is obtanied from C 2 n by adding n main diagonals. M 5

Exercises • N 14. Show that Pn can be obtianed from Mn by deleting and reataching two edges. • N 15. Use Tutte’s algorithm to draw the Petersen graph and use one of the pentagonal cycles C 5 as the peripheral regular pentagon with unit side length. Verify that the inner cycle is drawn as the pentagram. Determine its side.

Homework • H 1. Show that every graph can be embedded in ℝ 3. (Hint: place vertices on the helix curve (cos t, sin t, t) or even better on the curve (t, t 2, t 3). • H 2. Show that there is only one fullerene on 24 vertices. Draw its skeleton. • H 3. Prove that none of the Möbius ladders Mn is planar. • H 4. Use Tutte’s algorithm to draw the cube Q 3 and use the unit square for the outer face. What is the length of a side in the opposite, inner face?