Planar graphs Algorithms and Networks Planar graphs Can

Planar graphs Algorithms and Networks

Planar graphs • Can be drawn on the plane without crossings • Plane graph: planar graph, given together with an embedding in the plane • Many applications… • Questions: – Testing if a graph is planar – Finding a nice or good drawing of a planar graph • But what does that mean? – Solving problems for planar graphs 2 Planar graphs

Graph drawing / network layout • Applications: – Visually representing a network (e. g. , social network, organization structure, data bases (ERdiagrams), software (e. g. , UML-diagrams), flow charts, phylogenetic trees (biology, evolution), … – Design of “chip” layout (VLSI) –… 3 Planar graphs

Some notions • • 4 Faces Exterior face Interior faces Each edge is incident to 2 faces, except in special cases: Planar graphs

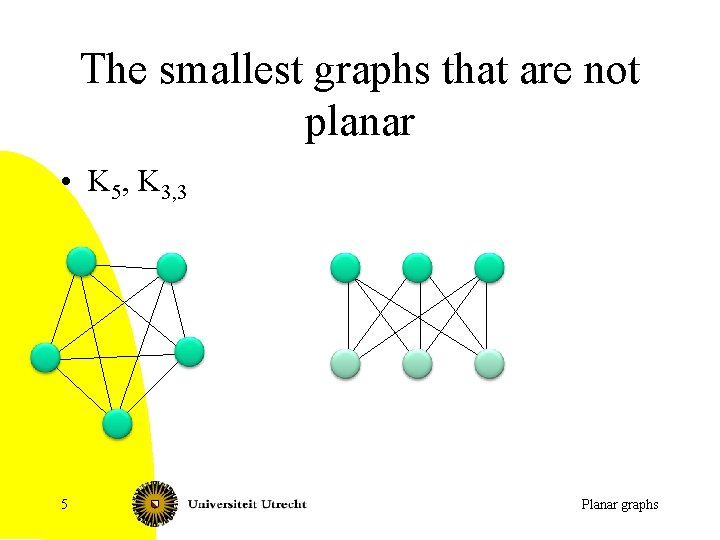
The smallest graphs that are not planar • K 5, K 3, 3 5 Planar graphs

Kuratowski / Wagner • Theorem (Kuratowski, Wagner, 193*) A graph is planar, if and only if it does not contain the K 5 and the K 3, 3 as a homeomorphic subgraph / as a minor. • H is a minor of G, if H can be obtained from G by a series of 0 or more deletions of vertices, deletions of edges, and contraction of edges. • Does not yield fast recognition algorithm! 6 Planar graphs

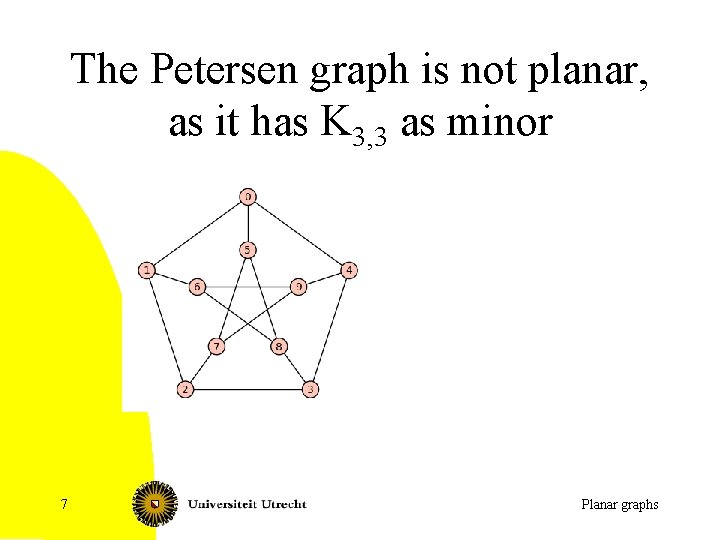
The Petersen graph is not planar, as it has K 3, 3 as minor 7 Planar graphs

Euler’s theorem • Theorem (Euler) Let G be a connected plane graph with n vertices, m edges, and f faces. Then n + f – m = 2. • Proof. By induction. – True if m=0. – If G has a circuit, then delete an edge and … – If G has a vertex v of degree 1, then delete v and … • … 8 Planar graphs

Euler’s theorem Corollaries • If G is a connected plane graph with no parallel edges and no self-loops, with n > 1, then m £ 3 n-6. – Every face `has’ at least three edges; each edge `is on’ two faces, or twice on the same face. • Every plane graph with no parallel edges and no self-loops has a vertex of degree at most 5. • Has algorithmic consequences… 9 Planar graphs

Duality • The dual G* of a plane graph G – A vertex in G* for each face of G – An edge in G* when faces share an edge in G 10 Planar graphs

Drawings of planar graphs • Different types • Vertices are: – Points in 2 -dimensional space – Rectangles, other objects • Edges are – – 11 Usual model Straight lines Curves Lines with bends Adjacencies or intersections of objects Planar graphs

Drawing planar graphs In steps: 1. Test if G is planar, and 2. Find for each vertex, a clockwise ordering of its incident edges, such that these orderings allow a planar embedding, and then 3. Assign coordinates to vertices 12 Planar graphs

Planarity testing: reduction to biconnected graphs • First, suppose G is biconnected. – G is biconnected, if for each vertex v, G-v is connected. – A biconnected component of G is a maximal subgraph that is biconnected. – A graph is planar, if and only if each of its biconnected components is planar. • Each biconnected component can be drawn with any vertex on its exterior face. • Build drawing of G by putting drawings of biconnected components together. • Easier non-constructive argument: G has a K 5 or K 3, 3 minor, iff a biconnected component of G has such a minor. 13 Planar graphs

Cycles with pieces • Take a cycle C in G. • Divide edges not on C of G into classes: – e and e’ in the same class if there is a path starting with e, ending with e’, using no vertices on C as intermediate points – A class forms a piece. • Pieces are – A single edge between two vertices on C – A connected graph with at least one vertex not on C 14 Planar graphs

Separating cycles • A cycle is separating if it has at least two pieces. • Plan: – Find separating cycle C (how? ) – Test for each piece + C if it is planar (recursion) – Determine for each piece if it has to be drawn inside or outside C (matching problem; details follow). 15 Planar graphs

Finding a separating cycle • • • Find a cycle C. If C separating: done. Otherwise, let P be the unique piece. If P is a path: G is planar: done. Otherwise: – Take two consecutive attachments v, w of P in the circular ordering of C, and let Q be the part of C between the attachments without another attachment. – Take a path R between v and w in P avoiding other attachments – C – Q + R is a separating cycle 16 Planar graphs

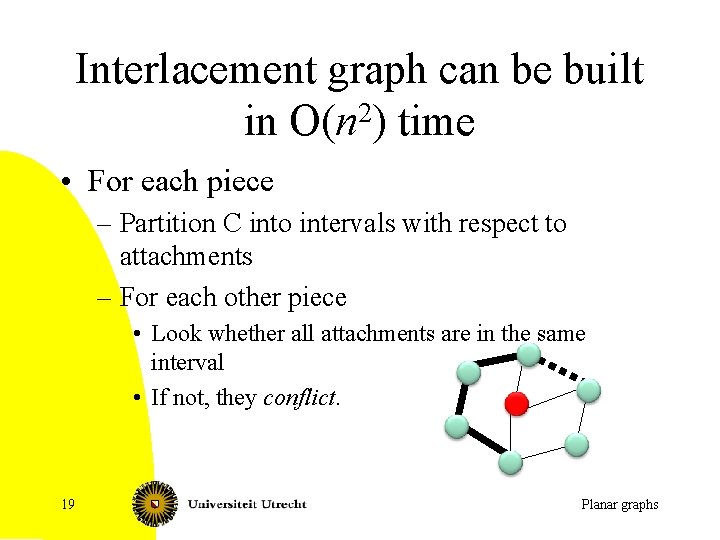
The interlacement graph • Pieces can be `inside’ or `outside’ the cycle • Build interlacement graph – Each piece is a vertex in interlacement graph – Pieces are adjacent, when they cannot be at the same side (look to attachments) 17 Planar graphs

Theorem • Let C be a separating cycle in G. G is a planar graph, if and only if – For each piece P, C+P is planar. – The interlacement graph is bipartite. Gives a polynomial time algorithm! 18 Planar graphs

Interlacement graph can be built in O(n 2) time • For each piece – Partition C into intervals with respect to attachments – For each other piece • Look whether all attachments are in the same interval • If not, they conflict. 19 Planar graphs

Algorithm • • • Find a cycle C Test if C is separating. If not, use method to build separating cycle C’. Find pieces of C’. Build interlacement graph. Test if interlacement graph is bipartite. If not: G is not planar, stop. • Otherwise, test for each piece P, recursively, if P+C’ is planar. 20 Planar graphs

Time • O(n 3). • Can be done faster: O(n) algorithms exist. • Finding clockwise orderings of edges per vertex can also be done: several details… 21 Planar graphs

Force directed methods • Method for arbitrary graphs • Uses physical analogy: – Force system – Method to find equilibrium state • Advantages: – Relatively easy to understand implement – Often reasonably nice results 22 Planar graphs

Springs and electrical forces method • Edges are springs • Vertices repel each other • Force on vertex: – fuv is force on spring – guv is repelling force 23 Planar graphs

Spring force • Assume some `wanted length’ of an edge luv. (E. g. , 1. ) • Spring wants to assume length luv; force is proportional to difference with luv. • Choose some stiffness of the spring kuv. ’ • Force in x-direction is (y-direction similar): 24 Planar graphs

Repelling force • Vertices are repelling particles • Follow inverse square law • k’uv is strength of repulsion (choose some number, e. g. , experimentally) • Repelling force of v in x-direction: Similar in y-direction 25 Planar graphs

Search for equilibrium • Position where all vertices have a force of 0 towards them (sum of spring and repelling forces) • Springs have lengths of edges go to desired length • Repelling has vertices not too close together 26 Planar graphs

Searching for equilibrium • Numerical techniques • Simple algorithm: – Take for each vertex a random position – Repeat: • Compute for each vertex its force • Move all vertices to new position depending on their forces Until in sufficient rest • Faster algorithms exist 27 Planar graphs

Barycenter method • Tutte, 1960 • Differences with force method – No repelling forces – luv = 0 – Stiffness is 1 – Vertices at exterior face get fixed positions 28 Planar graphs

Force on a vertex Where pu is the position of u on the plane If v is a free vertex 29 Planar graphs

Finding equilibrium • System of forces can be written as set of linear equations • Fast converging algorithms • For planar graphs, system can be solved in O(n 1. 5) time 30 Planar graphs

Barycenter draw pseudocode • Place all fixed vertices at corners of polygon around origin, and all free vertices on origin • Repeat – For each free vertex v do • x(v) = 1/degree(v) * S((u, v) in E) x(u) • y(v) = 1/degree(v) * S((u, v) in E) y(u) until sufficient convergence 31 Planar graphs

Theorem of Tutte • If G is a triconnected planar graph, then this method yields a planar drawing of G. – Assuming … – In practice, layers become smaller in the inside • Generalizations with more complicated forces sometimes also have this property • If G is not triconnected, then we can make it triconnected by adding edges 32 Planar graphs

Grid drawings • Many results on planar drawings, e. g. , • Theorem (Schnyder, 1990) Every planar graph G has a plane drawing, such that – Each edge is a straight line – Vertices are mapped to pairs of integers in {0, 1, …, n – 2} * {0, 1, …, n – 2} 33 Planar graphs

Many other results • Embeddings with small areas and few bends per edge • Drawings where vertices are represented by rectangles with an edge if rectangles touch • … 34 Planar graphs