MTRICA EM ESPAOS DE CURVATURA CONSTANTE mtrica de

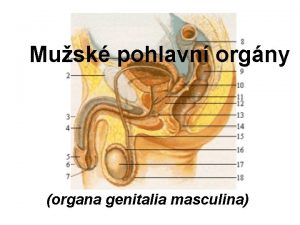
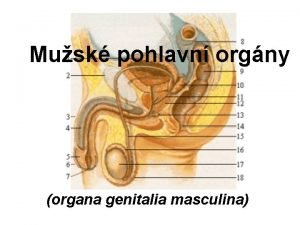
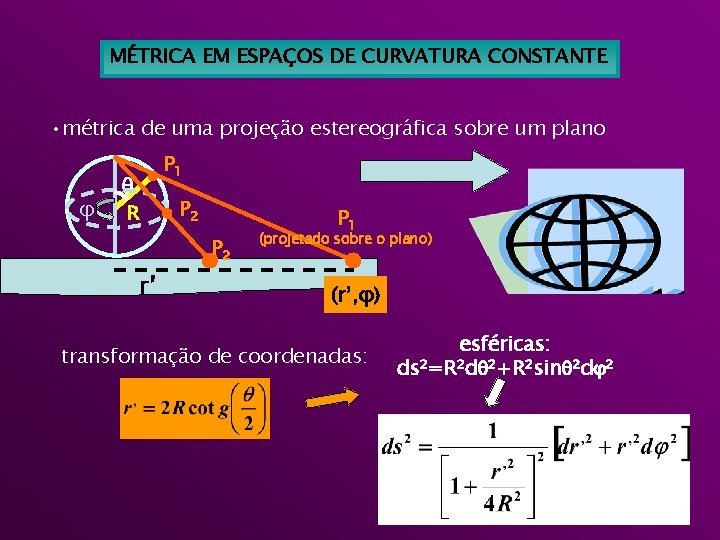
MÉTRICA EM ESPAÇOS DE CURVATURA CONSTANTE • métrica de uma projeção estereográfica sobre um plano P 1 R P 2 r’ P 1 (projetado sobre o plano) (r’, ) transformação de coordenadas: esféricas: ds 2=R 2 d 2+R 2 sin 2 d 2

1. perímetro de um círculo geodésico r’ é fixo dr’→ 0 2. área de um círculo geodésico

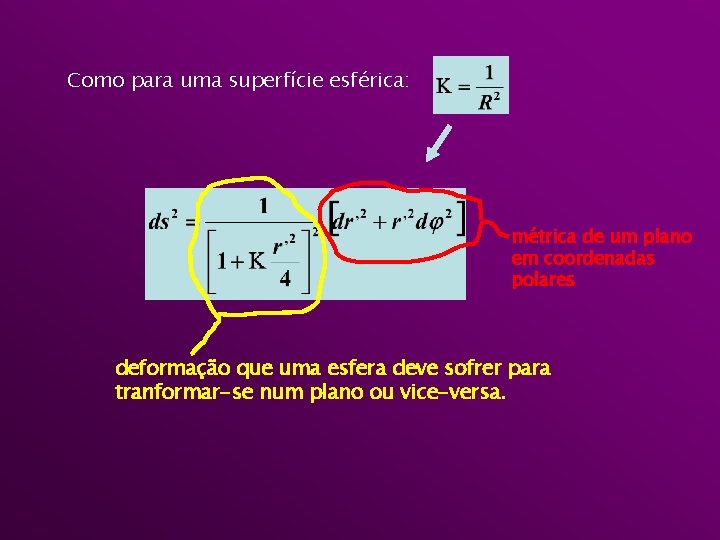
Como para uma superfície esférica: métrica de um plano em coordenadas polares deformação que uma esfera deve sofrer para tranformar-se num plano ou vice-versa.

reescrevendo x 1=r’cos x 2=r’sin Métrica válida para superfície de curvatura constante de qualquer sinal Forma generalizada a um no de dimensões n

Métricas 3 D para espaço de Ҝ constante Em coordenadas esféricas : x 1=r sin cos x 2=r sin x 3=r cos x 1 Forma + comum da métrica na cosmologia : Nota: a não é o raio próprio. x 3 r x 2

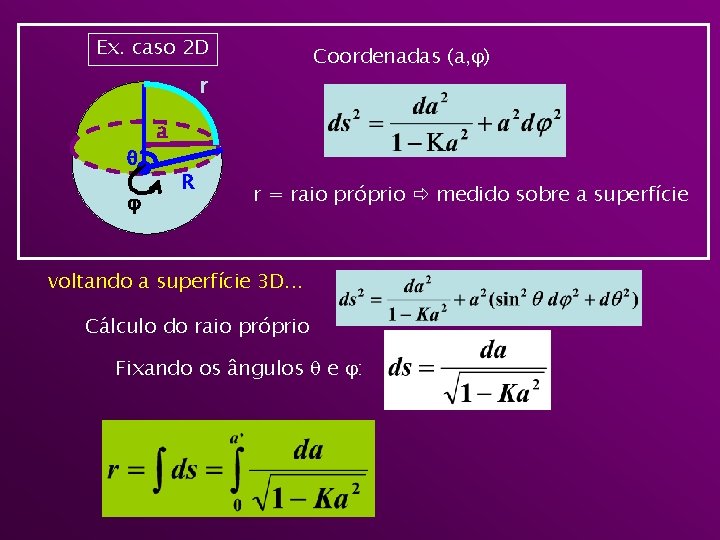
Ex. caso 2 D Coordenadas (a, ) r a R r = raio próprio medido sobre a superfície voltando a superfície 3 D. . . Cálculo do raio próprio Fixando os ângulos e :

APLICAÇÃO : HIPER-ESFERA Definição: espaços de curvatura positiva e constante com K > 0 e constante • raio próprio de uma esfera geodésica • área (de uma esfera de raio a dentro deste espaço)

A área de uma esfera de raio próprio espaço de Ҝ > 0 e constante: • r cresce: • quando área máxima quando r imersa em um

O volume de uma esfera de raio a dentro de um espaço Ҝ > 0 e constante para uma métrica ortogonal : Vmáx volume engloba todo o espaço de Ҝ > 0 e constante: volume finito ! espaço de Ҝ > 0 e constante é finito mas sem bordas. . .

Entretanto. . . Espaço de Ҝ 0 e constante são infinitos Ex. : uma esfera de volume V(a) dentro de um espaço de curvatura negativa Quando a→∞ V(a) →∞ Espaços deste tipo são ditos espaços infinitos Se Ҝ=0 , o volume de uma esfera em um espaço euclidiano é: V(a)=(4 /3)a 3 Tb quando a→∞ V(a) →∞

Espaços Riemannianos Definição: sempre que ds 2 for representado por uma forma diferencial qualdrática MÉTRICA RIEMANNIANA Ex. para uma superfície Característica importante: métrica riemanniana é localmente euclidiana !!

Demonstração: nas viz. De um ponto P 0, A 0, B 0 e C 0 são números: Fazendo: ds 2=dx’ 1+dx’ 2 Nas viz. De ponto sobre uma superfície Riemanniana a métrica pode ser aproximada como uma métrica euclidiana

Através de medidas de ângulos, perímetros ou áreas sobre uma dada superfície podemos medir a Ҝ Ir até as galáxias mais distantes e fazer medidas por triangulação (!!!!? ? )

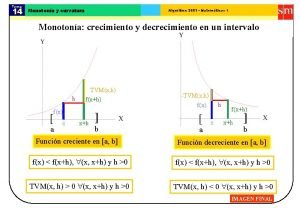
Número de galáxias num dado volume Galáxias uniformemente distribuídas: aumentando o raio aumenta o no de galáxias Se raio → 2 raio: K=0: N → 8 N k=+1: N < 8 N k=-1: N > 8 N

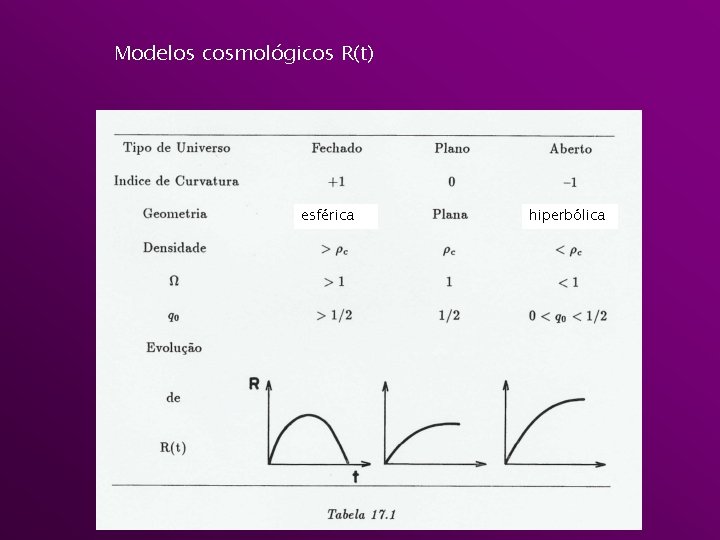
Modelos cosmológicos R(t) esférica hiperbólica