MonteCarlo meetodid 2 loeng Pseudojuhuslike arvude generaatorid Lineaarne

Monte-Carlo meetodid 2. loeng Pseudojuhuslike arvude generaatorid

Lineaarne kongruentne generaator Pseudojuhuslikud arvud vahemikus 0. . 1 saadakse valemiga: Lineaarse kongruentse generaatori abil on võimalik saada maksimaalselt m erinevat pseudojuhuslikku arvu: Kui xi = xj (j>i), siis paratamatult xi+1=xj+1 ja järelikult järgnevad pseudojuhuslikud arvud korduvad. Aga xi võimalikud väärtused on 0, 1, . . . , m-1. Kokku m erinevat väärtust. Peale m erineva pseudojuhusliku suuruse genereerimist pole teist võimalust – generaator hakkab samu arve uuesti otsast peale genereerima, sattub tsüklisse. Halb generaator võib aga samu arve kordama asuda ka märksa varem kui m arvu möödudes. . .

Näide halvast generaatorist

Teoreem Lineaarse kongruentse meetodi korral saavutatakse tsükli maksimaalne pikkus m parajasti siis, kui on täidetud järgmised tingimused: 1. suurim ühistegur SÜT(b, m)=1 2. (a-1) on iga algarvu kordne, millega jagub m (kui m jagub p-ga siis ka a-1 jagub p-ga) 3. Kui m jagub 4 -ga, siis peab ka a-1 jaguma 4 -ga.

Näide Generaator A a=5, b=1, m=8 1 6 7 4 5 2 3 0 1 6. . . . Lineaarse kongruentse meetodi korral saavutatakse tsükli maksimaalne pikkus m parajasti siis, kui on täidetud järgmised tingimused: 1. suurim ühistegur SÜT(b, m)=1 2. (a-1) on iga algarvu kordne, millega jagub m (kui m jagub p-ga siis ka a-1 jagub p-ga) 3. Kui m jagub 4 -ga, siis peab ka a-1 jaguma 4 -ga. B a=5, b=1, m=9 1 6 4 0 1 6. . . . C a=1, b=1, m=10 1 2 3 4 5 6 7 8 9 0. . . .

Märkus: multiplikatiivne generaator Multiplikatiivse generaatori korral on maksimaalne tsüklipikkus m-1. See saavutatakse ainult juhul, kui m on algarv ja a≠ 0 on nn lihtne juur: mistahes arvu m-1 algteguri p korral a(m-1)/p ei jagu arvuga m.

Soovitused (Handbook of Monte-Carlo Methods, D. P. Kroese; T. Taimre; Z. I. Botev): Näiteid m>261 ≈2*1018 Ei tohiks kasutada generaatoreid, mille m on esitatav kujul 2 p Min. STD a=75 b=0 SAS (UNIFORM) a=397204094 m=231 -1 b=0 m=231 -1 Visual Basic (ver 6 ja varasem): a=1140671485 b=12820163 m=224 MMIX (Knuth) a=6364136223846793005 b=1442695040888963407 m=264 Maple: a=427419669081, b=0, m=1012 -11 Pierre L'Ecuyer: a=243267374564284687042667403923350539132 b=0, m=2128 -159. . Vaata: http: //random. mat. sbg. ac. at/results/karl/server/node 5. html

Pikk periood ei taga veel head generaatorit a=1, b=1, m=mustmiljon Xi = 1, 2, 3, 4, 5, 6, 7, 8, 9, . . . Tuleks jälgida korrelatsiooni järjestikuste LKGgeneraatori poolt genereeritud arvude vahel. Sageli saab mõistliku generaatori valikuga a ≈ sqrt(m)

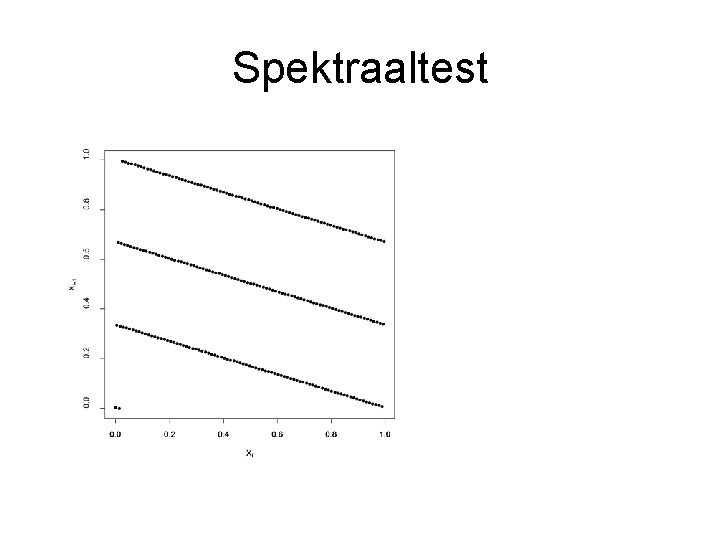
Spektraaltest

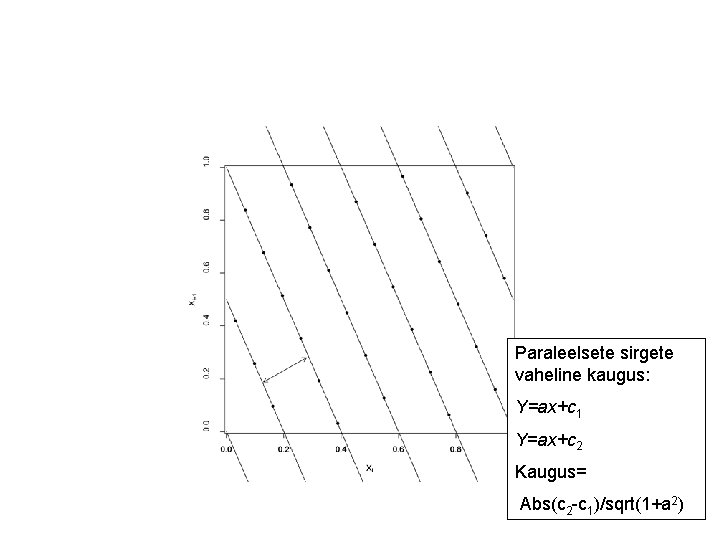
Paraleelsete sirgete vaheline kaugus: Y=ax+c 1 Y=ax+c 2 Kaugus= Abs(c 2 -c 1)/sqrt(1+a 2)

Sirged ise: Variant 1 y=ax+b-m*2 y=ax+b-m*3. . Variant 2. . .

d=0. 3162, 0. 1162, 0. 0790, 0. 0632 S=0. 1839, 0. 5003, 0. 7357, 0. 9196

Alternatiive I • Multiplikatiivsed-rekursiivsed generaatorid: Xi = (a 1 Xi-1 + a 2 Xi-2+. . . +ak Xi-k) mod m i=k, k+1, . . • LFSR (Linear feedback Shift Register Generator)

Alternatiive II • Kombineeritud generaatorid Periood ligikaudu 3*1057 Nimi: MRG 32 k 3 a

Alternatiive III • Blum-Shub generaator kus m=p*q, kus p ja q on suured algarvud, mille jääk jagamisel 4 -ga on 3 (Blum’i algarvud), näiteks: p = 1267650600228229401496703981519 q = 1267650600228229401496704318359 Igal iteratsioonil kasutatakse kõige väiksema biti väärtust – millistest pannakse kokku kasutatav pseudojuhuslik arv.