Regressioonanals Lineaarne regressioon Kui tunnuste X ja Y

Regressioonanalüüs

Lineaarne regressioon Kui tunnuste X ja Y vahel on tugev lineaarne korrelatsioon, siis on võimalik koostada lineaarne mudel, mis väljendab ühe tunnuse keskväärtuse sõltuvust teisest tunnusest. Ühe tunnuse (juhusliku suuruse) modelleerimisega teise tunnuse abil tegeleb regressioonanalüüs. Lineaarse regressiooni korral uuritakse sõltuvust kujul (1) kus a ja b on vähimruutude meetodi abil määratavad parameeetrid e. regressioonikordajad. Tegelikult vaadeldud Yi on valemiga (1) arvutatud väärtusest mõnevõrra (ei võrra) erinev:

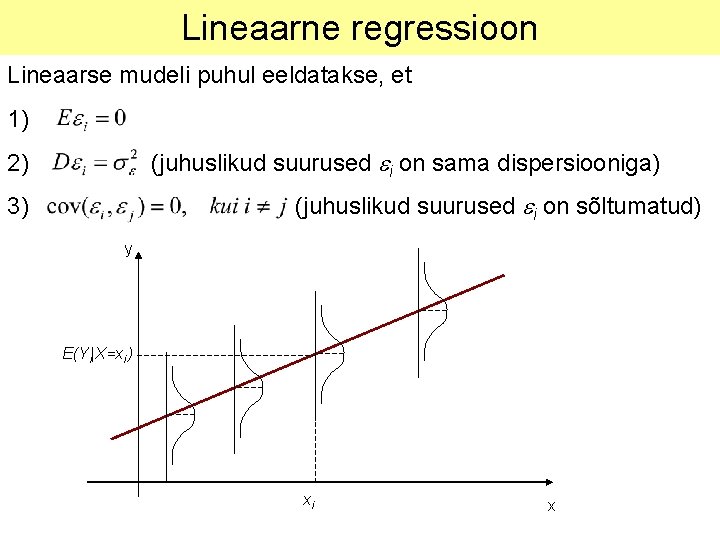
Lineaarne regressioon Lineaarse mudeli puhul eeldatakse, et 1) (juhuslikud suurused ei on sama dispersiooniga) 2) (juhuslikud suurused ei on sõltumatud) 3) y E(Yi|X=xi ) xi x

Vähimruutude meetod (I) y ^ y = a + bx yi ei ^ yi xi Hälbed: x ei = (a + bxi) - yi Hälvete ruutude summa: Vähimruutude meetodi idee kohaselt leitakse kahe muutuja funktsiooni G(a, b) miinimum.

Vähimruutude meetod (II) Esmalt leiame kriitilise punktid, võrdsustades osatuletised nulliga: summa diferentseerimise reegel liitfunktsiooni diferentseerimise reegel Lineaarne võrrand a ja b suhtes. Valimi põhjal leitavad konstandid

Vähimruutude meetod (III) Samuti peab kriitilises punktis nulliga võrduma osatuletis b järgi: Lineaarne võrrand a ja b suhtes. Saime kahest tundmatust ja kahest võrrandist koosneva lineaarse võrrandisüsteemi: Sellest süsteemist avaldame a ja b:

Vähimruutude meetod (IV) Kui süsteem on lahenduv, siis, leides teist järku osatuletised kriitilise punkti kohal, saab näidata, et selles punktis on funktsioonil G(a, b) miinimum. Regressioonisirge võrrand on avaldatav ka kujul millest on näha, et regressioonisirge läbib punkti nimetatakse korrelatsiooni keskpunktiks. , mida

Determinatsioonikordaja mõõdab, kui hästi regressioonisirge lähendab vaatlusandmeid. Selleks, et determinatsioonikordajat leida, arvutatakse: 1) mõõdetud väärtuste yi aritmeetiline keskmine ; 2) mõõdetud väärtuste yi koguvariatsioon ; 3) lineaarse regressioonimudeliga selgitatav variatsioon kus on lineaarse regressioonimudeli kohaselt arvutatud väärtus („silutud väärtus“) ; 4) variatsioon, mis ei ole selgitatav lineaarse regressiooniga:

Determinatsioonikordaja (II) Suurused on seotud valemiga 5) Determinatsioonikordaja on lineaarse regressioonimudeliga selgitatava variatsiooni ja koguvariatsiooni suhe Determinatsioonikordaja väärtus rahuldab võrratusi. ning ta väljendab, kui suur osa sõltuva muutuja Y kogumuudust on selgitatav sõltumatu muutuja X muuduga.

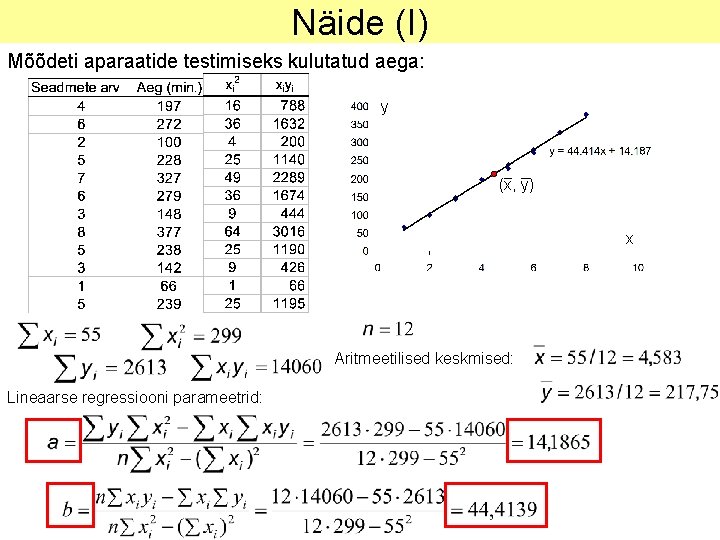
Näide (I) Mõõdeti aparaatide testimiseks kulutatud aega: y (x, y) x Aritmeetilised keskmised: Lineaarse regressiooni parameetrid:

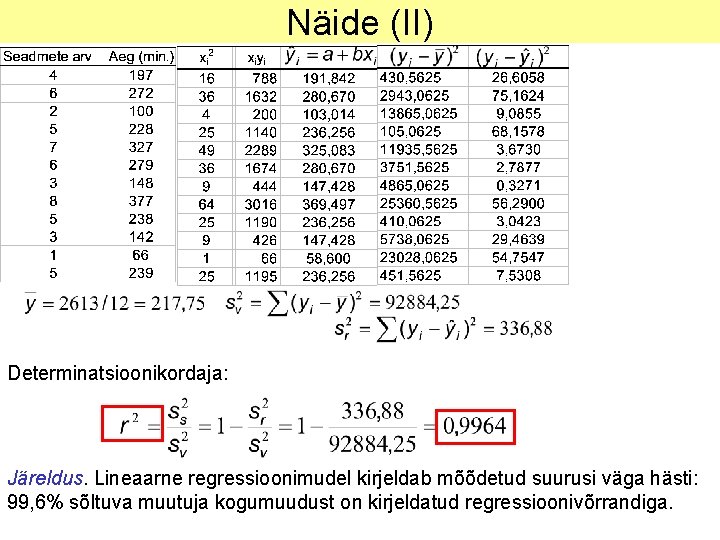
Näide (II) Determinatsioonikordaja: Järeldus. Lineaarne regressioonimudel kirjeldab mõõdetud suurusi väga hästi: 99, 6% sõltuva muutuja kogumuudust on kirjeldatud regressioonivõrrandiga.

Regressioonisirge parameetrite usalduspiirkonnad Regressioonisirge parameetrite a ja b usalduspiirkondade leidmiseks: 1) Leiame prognoosijäägi ei standardhälbe hinnangu: 2) Leiame parameetrite a ja b standardhälvete hinnangud: 3) Etteantud usaldusnivoo b puhul on a ja b usalduspiirkonnad: kus k = n – 2 ja kvantiil. a = (1 + b) / 2 ja t(k; a) on Studenti jaotuse

Näide Viimativaadeldud näites leidsime: n = 12 Leiame parameetrite a ja b 95%-lised usalduspiirid. 1) 2)

Näide (II) 3) 4) vabaliikme a 95%-lised usalduspiirid: 5) lineaarliikme kordaja b 95%-lised usalduspiirid:

Statistilised prognoosid ja nende usaldatavus Prognoosi punkthinnang: Prognoosi punkthinnangu standardhälve: Prognoosi usalduspiirid usaldunivooga b: kus a = (1 + b) / 2 ja k = n – 2 ja kvantiil. on Studenti jaotuse

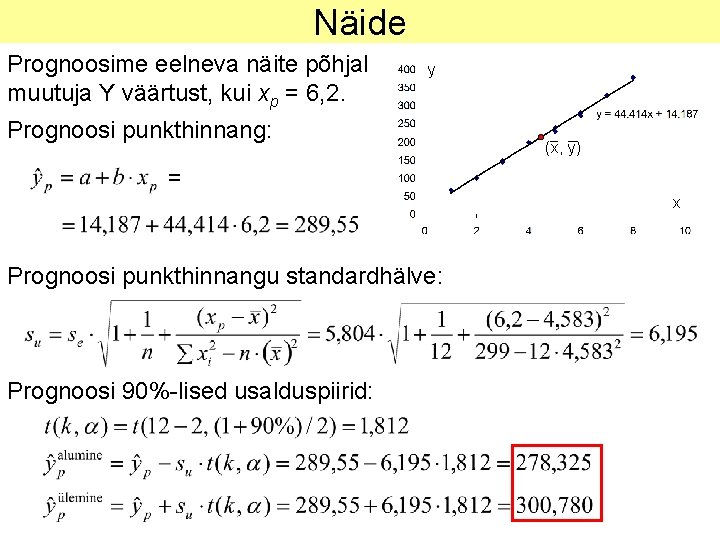
Näide Prognoosime eelneva näite põhjal muutuja Y väärtust, kui xp = 6, 2. y Prognoosi punkthinnang: (x, y) = x Prognoosi punkthinnangu standardhälve: Prognoosi 90%-lised usalduspiirid:

Multiregressioon (I) Kui sõltumatuid muutujaid on rohkem kui üks (näiteks X ja Z) ning nad on lineaarses korrelatiivses seoses sõltuva muutujaga Y, siis võib otsida üldkogumi regressioonimudelit kujul kus e on viga, mille keskväärtus Ee = 0. Üldkogumi regressiooni hindamiseks kasutatakse regressioonitasapinna võrrandit kus kordajad a, b ja c leitakse vähimruutude meetodi abil, minimiseerides hälvete ruutude summa

Multiregressioon (II) Parameetrite a, b ja c määramiseks saame lineaarvõrrandite süsteemi Mitmene determinatsioonikordaja arvutatakse analoogselt lihtregressiooni juhuga ning samad valemid kehtivad ka prognoosi täpsuse ning parameetrite usalduspiiride leidmiseks

Näide Mõõdetud suurused: X – ettevõtte reklaamikulud meedias; Z - ettevõtte reklaamikulud müügipunktis; Y – müügitulud. Koostame lineaarse mudeli S

Näide (II) Võrrandisüsteem a, b ja c määramiseks: Lahend: a = 2, 160; b = 3, 027; Mudel: c = 0, 699 Mitmene determinatsioonikordaja: