matematyk szkocki ur 22 kwietnia 1692 zm 5

- matematyk szkocki ur. 22 kwietnia 1692 - zm. 5 grudnia 1770 Zajmował się teorią szeregów nieskończonych i teorią krzywych algebraicznych trzeciego stopnia oraz opracował wzór Abrahama de Moivre’a na silnię n! Liczby Stirlinga zostały wprowadzone przez Jamesa Stirlinga w dziele „Methodus Differentialis” wydanym w Londynie w roku 1730.

- wzór pozwalający obliczyć w przybliżeniu wartość silni. Wzór ten daje dobre przybliżenie dla dużych liczb n. Formalnie:

dzielimy na:

- opisują ilość sposobów na rozmieszczenie n liczb w k cyklach, oznaczane są symbolem Czytamy: „k cykli n” lub rzadziej używanym symbolem: Na przykład istnieje 11 różnych sposobów na stworzenie 2 cykli z 4 elementów ( s(4, 2)): [1, 2, 3] [4], [1, 2, 4] [3], [1, 3, 4] [2], [2, 3, 4] [1], [1, 3, 2] [4], [1, 4, 2] [3], [1, 4, 3] [2], [2, 4, 3] [1], [1, 2] [3, 4], [1, 3] [2, 4], [1, 4] [2, 3]. Cykl singletowy (tzn. cykl składający się tylko z jednego elementu) zasadniczo odpowiada zbiorowi singletowemu (zbiór tylko z jednym elementem). Podobnie, 2 -cykl odpowiada 2 -zbiorowi, ponieważ [A, B] = [B, A], tak jak {A, B} = {B, A}. Ale istnieją różne 3 -cykle: [A, B, C] i [A, C, B]. Zauważmy, że 11 par cykli można uzyskać z poprzednio podanych (liczby drugiego rodzaju) siedmiu par zbiorów poprzez stworzenie dwóch cykli z każdego 3 -elementowego zbioru.

Przykład 1. Liczba sposobów podziału n obiektów na k niepustych, rozłącznych bloków z cyklicznym uporządkowaniem elementów na każdym bloku. Przykład 2. Liczba sposobów rozsadzenia n osób przy dokładnie k okrągłych stolikach, jeśli przy stolikach może siedzieć nieograniczona liczba osób i liczy się sposób ich usadzenia przy danym stoliku (czyli to, kto obok kogo siedzi) /elementy zbioru-osoby cykle permutacji-stoliki/ Dla lepszego rozróżnienia liczb odpowiednio pierwszego i drugiego rodzaju rozpatrzmy sytuację: Mamy prostokątne stoliki ustawione w rzędzie. Sadzamy przy nich osoby tak, że wszystkie siedzą po tej samej stronie wszystkich stołów (czyli tworzą 'siedzący' szereg). Wtedy: to liczba rozsadzeń n osób przy k stolikach (przy każdym stoliku co najmniej jedna osoba) takich, że przy lewym końcu stolika (z perspektywy siedzących) siedzi najstarsza spośród osób przy tym stoliku, a pozostałe osoby siedzą w dowolnej kolejności po jej prawej stronie. to liczba rozsadzeń n osób przy k stolikach (przy każdym stoliku co najmniej jedna osoba) takich, że osoby przy każdym stoliku siedzą w kolejności od najstarszej (przy lewym końcu stolika) do najmłodszej (przy prawym końcu).

przy założeniach Przyjmuje się, że jeżeli k > n, to Pochodzenie wzoru rekurencyjnego: Przyjmując za znaczenie liczb Stirlinga pierwszego rodzaju ilość rozmieszczeń n–liczb w k–cyklach, łatwo jest pokazać pochodzenie rekurencyjnej zależności między nimi. Wystarczy wybrać dowolną liczbę i rozpatrzyć ilość pozostałych cykli. Jeżeli ta liczba była w cyklu, składającym się z jednego elementu, to pozostałe n-1–liczb jest rozmieszczonych w k-1–cyklach, zaś dodanie jednej cyfry następuje w jeden sposób, poprzez stworzenie nowego cyklu. Jeżeli liczba była w liczniejszym cyklu, to pozostałe n-1–liczb jest rozmieszczonych w k–cyklach, zaś dodatkową liczbę można wstawić do dowolnego cyklu w dowolny sposób, czyli "obok" każdej liczby, a liczb jest n-1, co oznacza n-1–sposobów umieszczenia liczby w tym przypadku. Rekurencyjna zależność jest sumą obu przypadków. Warto przy tym zauważyć, że zbiór n–liczb można ustawić w 0 cykli na 0 sposobów, oraz 1 liczbę w 1 cyklu na 1 sposób.

Liczby Stirlinga pierwszego rodzaju bywają także definiowane jako współczynniki, występujące przy zamianie potęg malejących (silni dolnej) na zwyczajne potęgi: Przy zamianie normalnych potęg na potęgi rosnące (silnię górną) występuje zależność:

s(n, k)=(n-1) s(n-1, k)+s(n-1, k-1) 11=3 * 3 + 2

Po zastosowaniu podstawowych rekurencji oraz (liczby Stirlinga pierwszego rodzaju) (liczby Stirlinga drugiego rodzaju) poza ich kombinatoryczne znaczenie, czyli uznając, że są prawdziwe dla wszystkich n, k całkowitych przy dodatkowym założeniu S(0, k) = s(0, k) = [k=0] i S(n, 0) = s(n, 0) =[n=0] otrzymujemy trójkąt Stirlinga dla cykli, który pojawia się powyżej trójkąta Stirlinga dla podzbiorów (i odwrotnie!) za to oba rodzaje liczb Stirlinga powiązane są wyjątkowo prostą zależnością: s(n, k) = S(-k, -n), dla całkowitych k, n.

- opisują ilość sposobów podziału zbioru n elementowego na k niepustych (parami rozłącznych) podzbiorów, które w sumie dają cały zbiór, zatem opisują ilość k-blokowych partycji zbioru n. (NIEUJEMNE) Czytamy: "k podzbiorów n" Liczby Stirlinga II rodzaju oznaczane są symbolem: lub: S(n, k) Spełniają one związek rekurencyjny postaci: przy założeniach Przyjmuje się, że jeżeli k > n, to :

Ilekroć poniżej będziemy mówiły o przypisywaniu ludzi do stolików lub do pokoi, to przyjmujemy, że: -osoby są rozróżnialne; -pokoje są rozróżnialne, np. ponumerowane; -stoliki są nierozróżnialne, tzn. identyczne Przykład 1. Liczba rozmieszczeń n różnych przedmiotów (np. kulek, każda innego koloru) do m identycznych pudełek, gdy zajętych jest dokładnie k pudełek równa się Podobnie : n osób możemy rozsadzić przy dokładnie k stolikach na sposobów, jeśli przy stoliku może siedzieć nieograniczona liczba osób i sposób ich usadzenia przy danym stoliku nie ma znaczenia. Przykład 2. Liczba będąca iloczynem n różnych liczb pierwszych może być przedstawiona w postaci iloczynu k różnych czynników (niekoniecznie będących liczbami pierwszymi) na sposobów. Przykład 3. Rozważmy permutacje n liczb. Każda permutacja może być przedstawiona w postaci iloczynu rozłącznych cykli. Weźmy tylko te permutacje, których cykle (a konkretnie elementy tych cykli) są uporządkowane w pewien konkretny sposób, np. w porządku rosnącym. Permutacji n liczb spełniających te własność i rozkładających się na k cykli jest

Niekiedy liczby Stirlinga drugiego rodzaju są definiowane jako współczynniki, występujące przy zamianie normalnych potęg na potęgi malejące (silnię dolną). Zachodzi wówczas zależność: " x do m-tej ubywającej " m czynników Dla wykładników mniejszych od 0 silnię dolną definiuje się jako:

Przyjmując za znaczenie liczb Stirlinga drugiego rodzaju ilość sposobów podziału zbioru n–elementowego na k–podzbiorów niepustych, łatwo jest uzasadnić rekurencyjną zależność. Rozpatrzymy zbiór n–liczb, i wybierzmy jedną z nich. Jeżeli ta liczba stanowiła jednoelementowy podzbiór, to pozostałe n-1–liczb będzie podzielone na k-1–podzbiorów, zaś jedną liczbę można dodać na jeden sposób, jako kolejny podzbiór. Jeżeli liczba była elementem liczniejszego podzbioru, to pozostałe n-1–liczb zostało podzielone na k–podzbiorów, zaś dodatkową liczbę można dołączyć do każdego z podzbiorów, których jest k. Można to więc w tym przypadku zrobić na dokładnie k–sposobów. Rekurencyjna zależność jest sumą obu przypadków. Warto przy tym zauważyć, że zbiór n–liczb można podzielić na 1 podzbiór na 1 sposób, a także na n–podzbiorów na 1 sposób. Za pomocą funkcji tworzących udowodnimy teraz jawny wzór na

* Niech - oznacza liczbę k blokowych partycji zbioru n elementowego, czyli ilość możliwości podziału zbioru n elementowego na k niepustych podzbiorów. Mamy zbiór n elementowy, musimy utworzyć k niepustych (parami rozłącznych) podzbiorów, które w sumie dadzą nam nowy n elementowy zbiór. Rozpatrzmy np. pierwszy element: 1. może być on sam w którymś podzbiorze, a wtedy reszta (n-1 elementów) będzie rozłożona w k-1 niepustych (parami rozłącznych) podzbiorów, czyli na sposobów. 2. albo być w którymś z k podzbiorów, które zostały wcześniej podzielone na k niepustych podzbiorów, czyli sposobów jest 3. Sumując te dwa przypadki otrzymujemy: 4. (1) 5. ( Rekurencja obejmuje również ujemne wartości jak i np. przypadki kiedy k>n, ale wtedy naturalnie =0 )

* Funkcje tworzące Mamy możliwość wyboru czy będziemy obliczać funkcję tworzącą po zmiennej k czy n czy k i n jednocześnie (funkcje tworzące wielu zmiennych). My zajmiemy się tylko drugą z nich. Niech: Funkcja Czyli zgodnie z zasadą mnożymy (1) stronami przez i sumujemy po wszystkich n.

dla k>0 (przyjmujemy B 0 (x)=1) Zauważamy iż (2) można zapisać jako : Wyciągnijmy xk rozłóżmy na ułamki proste Szukamy teraz współczynników Ai , jeśli pomnożymy przez 1 -rx i podstawimy za , wszystkie po prawej wyzerują się i znajdziemy Ar i (2)

Wróćmy do funkcji tworzącej Szukamy współczynników przy xn w rozwinięciu funkcji , zauważmy że w liczniku występuje xk czyli właściwie szukamy współczynników przy xn-k funkcji Zapiszmy to formalnie: = = Szukamy współczynnika przy zmiennej x, wszystko co jej nie zawiera to jakby stała czyli można zapisać: A teraz, wiemy że Zatem: czyli No i mamy jawny wzór na liczbę k-blokowych partycji zbioru n-elementowego: =

S(n, k)=S(n-1, k-1)+k S(n-1, k) 7= 1+2*3

Uzasadnienie: Z każdego n-elementowego zbioru można stworzyć n!/n = (n-1)! różnych n-cykli, n>0. (Istnieje n! permutacji, a każdy n-cykl występuje n razy, bo każdy z jego elementów może być wypisany jako pierwszy. ) Zatem otrzymujemy tezę. Jest to znacznie więcej niż którą otrzymaliśmy w przypadku liczb podzbiorowych Stirlinga. Uzasadnienie: Ponieważ każdy podział na niepuste podzbiory prowadzi do co najmniej jednego ustawienia w cykl, liczba cykli musi być co najmniej tak duża jak liczba podzbiorów. Równość zaś zachodzi wyłącznie wtedy, gdy wszystkie cykle są albo singletonami, albo dubletonami (wtedy cykle równoważne podzbiorom) Zatem: s(n, n) = S(n, n) , co daje 1.

Uzasadnienie: Ponieważ każdy podział na niepuste podzbiory prowadzi do co najmniej jednego ustawienia w cykl, liczba cykli musi być co najmniej tak duża jak liczba podzbiorów. Równość zaś zachodzi wyłącznie wtedy, gdy wszystkie cykle są albo singletonami, albo dubletonami (wtedy cykle równoważne podzbiorom). Zatem: s(n, n) = S(n, n) oraz s(n, n-1) = S(n, n-1), co w każdym z przypadków daje 1. (Liczba sposobów ustawienia n obiektów w n-1 cykli lub podzbiorów odpowiada liczbie sposobów wybrania dwóch obiektów, które będą w tym samym cyklu lub podzbiorze. ) Uzasadnienie: Ponieważ każda permutacja definiuje układ cykli (i odwrotnie, każdy układ cykli permutację), jest liczbą permutacji n obiektów, które zawierają dokładnie k cykli. Jeżeli zsumujemy ją po wszystkich k, dla całkowitych i nieujemnych n musimy otrzymać całkowitą liczbę permutacji. Np. : 6+11+6+1=24=4!

Związek liczb Stirlinga i liczb Bella Liczba Bella dla liczby naturalnej n (ozn: Bn) to liczba podziałów zbioru {1, . . . , n}. Bn = 1 1 2 5 15 52 203 877 4140 21147 S(n, k)

Związek pomiędzy liczbami Stirlinga II rodzaju i funkcjami z X na Y

Niech X i Y będą zbiorami skończonymi, |X|= n i |Y| = m. |X| |Y| Ile jest wszystkich funkcji całkowitych ze zbioru X w Y ? m*(m 1)*. . . *3*2*1 Ile jest różnych funkcji całkowitych różnowartościowych ? Ile jest funkcji całkowitych z X na Y ? Zauważmy, że jeśli mamy podział zbioru X na k części, to przypisując tym częściom elementy zbioru Y określamy funkcję z X na Y.

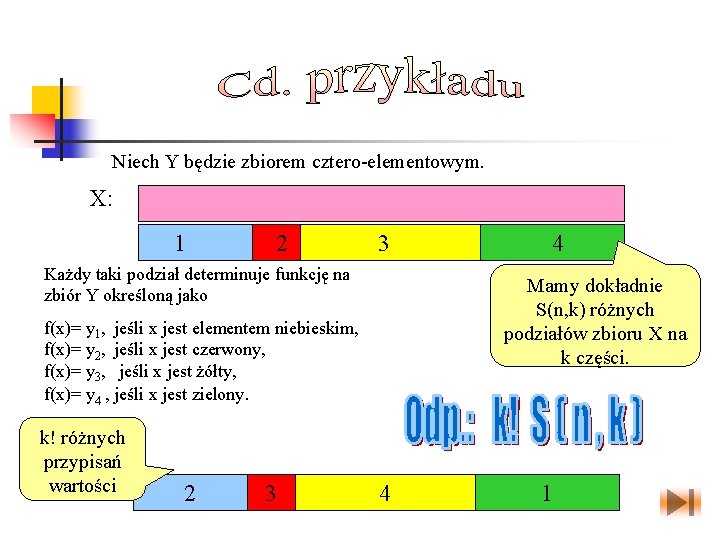
Niech Y będzie zbiorem cztero-elementowym. X: 1 2 3 Każdy taki podział determinuje funkcję na zbiór Y określoną jako Mamy dokładnie S(n, k) różnych podziałów zbioru X na k części. f(x)= y 1, jeśli x jest elementem niebieskim, f(x)= y 2, jeśli x jest czerwony, f(x)= y 3, jeśli x jest żółty, f(x)= y 4 , jeśli x jest zielony. k! różnych przypisań wartości 2 3 4 4 1

PRZYGOTOWAŁY: • Edyta Kordowska • Katarzyna Młodzikowska • Agnieszka Potaś