Lineris programozs Definci Olyan matematikai programozsi feladatot neveznk

Lineáris programozás • Definíció: Olyan matematikai programozási feladatot nevezünk lineáris programozási feladatnak, amelyekben az L halmazt meghatározó feltételek első fokú egyenletek és egyenlőtlenségek, a célfüggvényük lineáris, és a bennük szereplő változók valós számértéket vehetnek fel.

Maximumfeladat • Definíció: Maximumfeladatról akkor beszélünk, ha egyenlőtlenségei értelműek és a célfüggvény maximuma jelenti az optimumot. • Alapforma kanonikus forma • a) x 0, u 0 • b) A ·x b A·x+u=b • c) z = c. T · x max.

Normál maximumfeladat • Definíció: Egy maximumfeladatot normálfeladatnak nevezzük akkor, ha b 0 feltétel is teljesül. • Alapforma kanonikus forma • a) x 0, b 0 x 0, u 0, b 0 • b) A · x b · Ax+u=b • c) c. T · x max.

Módosított normálfeladat • Definíció: Egy modellt módosított normálfeladatnak nevezzük, ha egyenlőtlenségei értelműek, tartalmaz egyenleteket és célfüggvény maximumát keressük, továbbá a b 1 és b 2 vektorok minden koordinátája nemnegatív. • Alapforma kanonikus forma • a) x 0, b 1 0, b 2 0 x 0, u 0, b 1 0, b 2 0 • b) A 1 · x b 1 A 1 · x + u = b 1 • A 2 · x = b 2 • c) z = c. T · x max.

Általános feladat • Definíció: Egy lineáris modellt általános feladatnak nevezünk, ha feltételei között a kapacitások (b) nemnegativitása mellett relációk is szerepelnek és maximum a cél • alapforma kanonikus forma • a) x 0, u 0, v 0, • b) A 1 · x b 1, b 1 0 A 1 · x + u = b 1 0 • A 2 · x = b 2 0 • A 3 · x b 3 0 A 3 · x v = b 3 0 • c) z = c. T · x max.

Példa általános feladatra • a) x 1, x 2, x 3 ≥ 0 • b) 5 x 2 + 5 x 3 ≤ 80 • x 1 + x 2 x 3 = 10 • x 1 + x 2 + x 3 ≥ 18 • c) z =10 x 1 +30 x 2 +10 x 3 max • Minden lineáris modell felírható normál, módosított normál, vagy általános feladatként.

LP feladatok grafikus megoldása • Egy optimális megoldás esete • Nézzük a következő feladatot: a) x 1, x 2 0 • b) x 1 + x 2 70 • x 1 50 • x 2 40 • x 2 10 • c) z = 2 x 1 + x 2 maximum

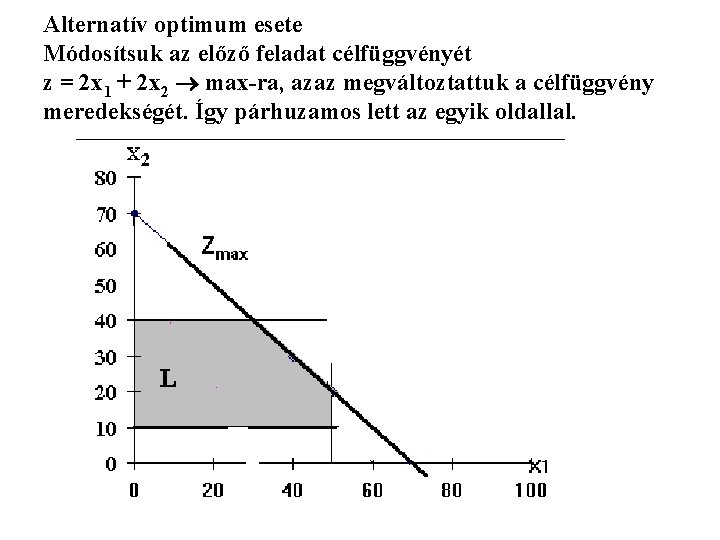
Alternatív optimum esete Módosítsuk az előző feladat célfüggvényét z = 2 x 1 + 2 x 2 max-ra, azaz megváltoztattuk a célfüggvény meredekségét. Így párhuzamos lett az egyik oldallal.

Célfüggvény nem korlátos • • A feltételeink legyenek a következők: a) x 1, x 2 0 b) 2 x 1 + x 2 60 x 2 20 x 1 − x 2 20 c) z = 3 x 1 + 4 x 2 max. Az L halmaz felülről nem korlátos. Ezért a célfüggvénynek nincs maximuma, hiszen a célfüggvény bármilyen értéket is felvehet az L halmazon, azaz a célfüggvény nem korlátos.

Ellentmondó feltételek esete • • • Adottak a következő feltételek: a) x 1, x 2 0 b) 2 x 1 + 4 x 2 200 2 x 1 + 2 x 2 80 c) z = 3 x 1 + x 2 max. Az egyenlőtlenségek által meghatározott félsikoknak nincs közös részük. Nincs egyetlen olyan pont sem, amely minden feltételnek eleget tenne. Ilyenkor azt mondjuk, hogy az L halmaz üres, így a feladatnak nincs megoldása.