Matematikai algoritmusok Sir Isaac Newton 1642 1727 Eratoszthensz

Matematikai algoritmusok Sir Isaac Newton 1642 - 1727 Eratoszthenész k. e. 276 – k. e. 194 etett, Alexandriai Euklidész k. e. 300 körül „A ge omet riáho leh z nem t r é z a vezet ) m (Euk on tta t a király w h l t e i á d l N ( é b s ”. b i út. ” z e ) m z llta ess á m n s á i l l alaha óriások vá „Aki azt mondja, nem szereti a matematikát, „Ha v mert az tulajdonképpen azt mondja, nem szeret gondolkozni. ” „A sem (Rényi Alfréd) miből e gy új, m ás v Kocsis Imre (Bolyai ilágot terem tettem János). ” Illyés Gyula Gimnázium Dombóvár

Válaszd ki valamelyik algoritmust! Az eratoszthenészi szita Az euklideszi algoritmus Newton gyökvonó algoritmusa A vetítés vége

Az eratoszthenészi szita A prímszámok előállításának ma is használt módszere Eratoszthenész görög matematikustól származik. Az elnevezés utal az eljárás lényegére, mivel az 1 -től n-ig felírt egész számok közül „kiszitáljuk” az összetett számokat. Amely számok fennmaradnak a „szitán” (az 1 kivételével) azok a prímek. Az eljárás: 1. Írjuk fel a számokat 1 -től n-ig, (itt például 100 -ig) egyesével. 2. Keressük meg az első olyan 1 -nél nagyobb számot, amelyik még nincs sem kihúzva, sem bekarikázva. Elsőként ez a 2. 3. Ezután húzzuk ki ennek többszöröseit, őt pedig karikázzuk be. 4. Ismételjük meg a második lépéstől újra az eljárást. Természetesen egy összetett szám többször is kihúzásra kerülhet. 5. Az algoritmus akkor álljon le, ha a második lépésnél talált szám négyzete már nagyobb, mint n. 6. Nyilván elegendő csupán az 1 és közötti p prímekkel elvégezni a szitálást, mivel ha valamely a szám n-nél kisebb és összetett, akkor van -nél kisebb prím osztója. A 6. pont bizonyítása: Tehát beláttuk, hogy egy szám osztópárjai közül a nem nagyobb, legfeljebb akkora, mint a szám négyzetgyöke!

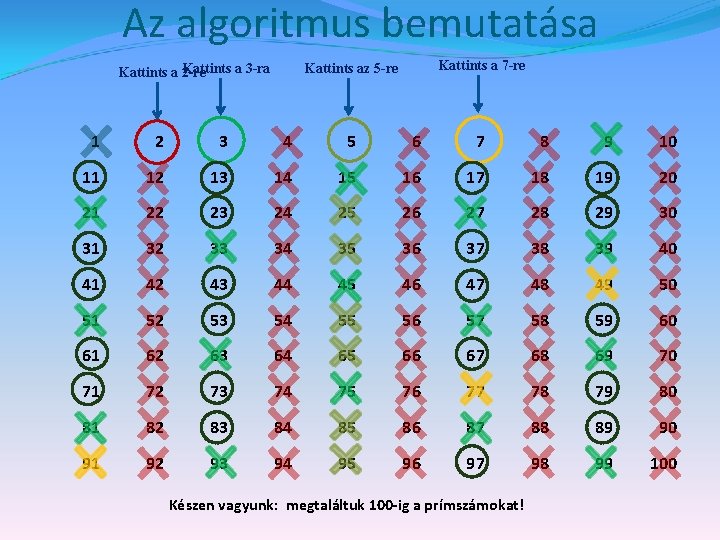
Az algoritmus bemutatása Kattints a 3 -ra Kattints a 2 -re Kattints a 7 -re Kattints az 5 -re 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 Készen vagyunk: megtaláltuk 100 -ig a prímszámokat!

Az algoritmus gyakorlása Gyakorlás módban a „szitálásra” alkalmas szám kiválasztása után a többszörösein kattints! (n és k maximuma 10)

Az algoritmus kódolása C++ nyelvű program Pszeudokód ciklus i=0 -tól n-ig termszamok[i]=i termszamok[1]=0, mert az 1 nem prím ciklus i=2 -től az n szám gyökéig) { j=i; Ha j<n ÉS termszamok[i] nem 0 { ciklus amíg j+i<n { j=i+i termszamok[j]=0 } } } void prim(int n) { int* termszamok; termszamok=new int[n]; for (int i=0; i!=n; i++) //az n elemű tömb feltöltése a természetes számokkal { termszamok[i]=i; } termszamok[1]=0; // Az 1 nem prím float r=n; //elegendő az n gyökéig vizsgálni float gyok=sqrt(r); for (int i=2; i<gyok; i++) { j=i; if (j<n && termszamok[j]!=0) { while (j+i<n) // i többszöröseit sorban kinullázzuk { j=j+i; termszamok[j]=0; // A tömb nem 0 elemei éppen a prímek } } delete[] termszamok; } Feladatok: Vissza a menühöz! 1. Mutassuk meg, hogy n szám prímtényezős felbontásában legfeljebb log 2 n tényező szerepel! 2. Bizonyítsuk be, hogy tetszőleges pozitív egész k szám esetén létezik k darab egymás után következő összetett szám!

Euklideszi algoritmus Az egyik legismertebb ókori algoritmus. Euklidész írta le a módszert két természetes szám legnagyobb közös osztójának meghatározására. Ezt a módszert nevezzük Euklideszi algoritmusnak. A maradékok szigorúan monoton csökkenő sorozata A maradék véges sok lépés után nulla lesz, hiszen amíg nem nulla, addig minden lépésben legalább eggyel csökkenni fog, tehát az utolsó lépésnél: A keresett legnagyobb közös osztó rn azaz az utolsó nem 0 maradék.

Az algoritmus helyességének bizonyítása Az a és b bármely közös osztója osztja az r 1 -et is hiszen és két szám közös osztója a különbségüket is osztja Hasonlóan b és r 1 bármely közös osztója osztja a-t is és két szám közös osztója az összegüket is osztja hiszen Ezekből következik, hogy a és b közös osztói megegyeznek b és r 1 közös osztóival, és így a legnagyobb közös osztójuk is azonos: (a, b) = (b, r 1) Ez a gondolatmenet minden lépésre ugyanígy megismételhető, azaz mivel: Az előzőek alapján tehát:

Az Euklideszi algoritmus működése 1. lépés: a nagyobbat osztjuk a kisebbel maradékosan További lépések: az osztót osztjuk tovább a maradékkal a = 174 osztandó b = 96 174: 96 hányados maradék 96 1 78 96: 78 78 1 18 78: 18 18 4 6 3 0 18: 6 174 osztó A végét jelzi A két szám legnagyobb közös osztója az utolsó nem 0 maradék: 6

Az algoritmus gyakorlása Gyakorold, és ellenőrizd a munkádat!

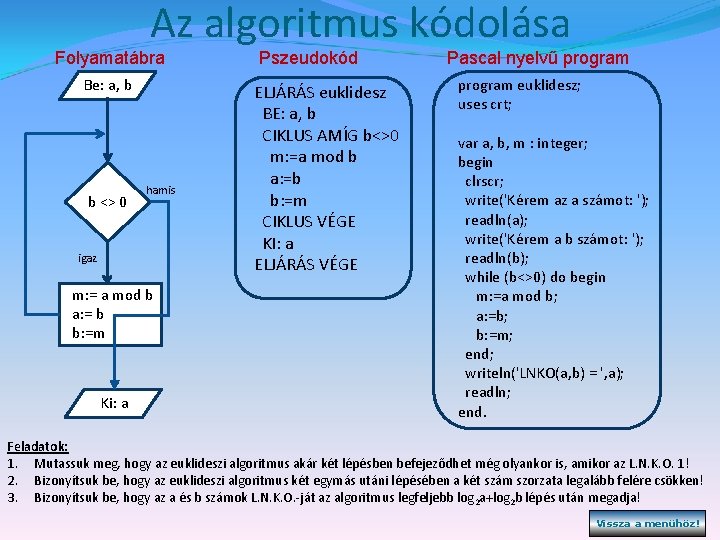
Az algoritmus kódolása Folyamatábra Be: a, b b <> 0 hamis igaz m: = a mod b a: = b b: =m Ki: a Pszeudokód ELJÁRÁS euklidesz BE: a, b CIKLUS AMÍG b<>0 m: =a mod b a: =b b: =m CIKLUS VÉGE KI: a ELJÁRÁS VÉGE Pascal nyelvű program euklidesz; uses crt; var a, b, m : integer; begin clrscr; write('Kérem az a számot: '); readln(a); write('Kérem a b számot: '); readln(b); while (b<>0) do begin m: =a mod b; a: =b; b: =m; end; writeln('LNKO(a, b) = ', a); readln; end. Feladatok: 1. Mutassuk meg, hogy az euklideszi algoritmus akár két lépésben befejeződhet még olyankor is, amikor az L. N. K. O. 1! 2. Bizonyítsuk be, hogy az euklideszi algoritmus két egymás utáni lépésében a két szám szorzata legalább felére csökken! 3. Bizonyítsuk be, hogy az a és b számok L. N. K. O. -ját az algoritmus legfeljebb log 2 a+log 2 b lépés után megadja! Vissza a menühöz!

Newton-féle gyökvonó algoritmus A Newton módszer egy approximációs (közelítés; ismeretlen mennyiségnek közelítő pontossággal történő meghatározására szolgáló eljárás) eljárás, amelynek alapvető ötlete, hogy a függvény egyik x*gyökéhez „közeli” x 0 pontot ismerve próbálja meghatározni az f(x) függvény egy x* gyökét. A kezdő becslésünk legyen x 0, majd a P 0(x 0; f(x 0)) pontban húzzunk érintőt a görbéhez. Ez az x tengelyt az x 1 pontban metszi. Ez az x 1 már jobb közelítésnek látszik, mint az x 0 volt. Ezután húzzunk újabb érintőt a P 1(x 1; f(x 1)) pontban. Ez az x tengelyt az x 2 pontban metszi. És így tovább. A kapott x 0, x 1, x 2, … pontok egyre jobb közelítései lesznek az x* gyöknek. Hogyan közelítsük meg az x* gyököt egyre jobban?

Newton nevezetes képlete Az x 1 x 0 P 0 háromszögben: Ez a görbe P 0 ponthoz tartozó érintőjének az iránytangense. Ez pedig az f függvény differenciálhányadosának az értéke az x 0 helyen: A két egyenletből: Átrendezve: Ezt a további lépésekre is alkalmazva: A végén Newton nevezetes formulája általánosan:

A négyzetgyök „a” meghatározása Az előző eredményünket alkalmazzuk a meghatározására Tehát az alkalmazandó Newton-képletben a jobboldal: A szükséges indexeket is kitéve a teljes egyenlet: Átalakítva: Legyen a=2, ekkor x 0=2, és: Négyzetük sorban: Egyre közelebb van a 2 -höz!

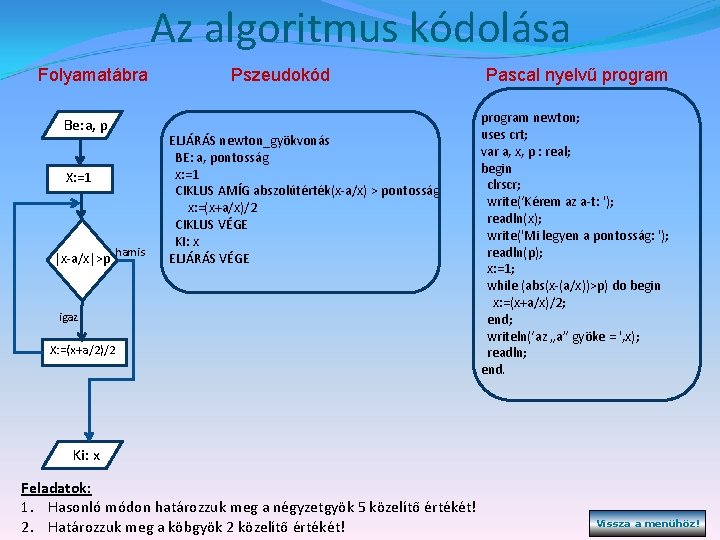
Az algoritmus kódolása Folyamatábra Be: a, p X: =1 |x-a/x|>p hamis Pszeudokód ELJÁRÁS newton_gyökvonás BE: a, pontosság x: =1 CIKLUS AMÍG abszolútérték(x-a/x) > pontosság x: =(x+a/x)/2 CIKLUS VÉGE KI: x ELJÁRÁS VÉGE igaz X: =(x+a/2)/2 Pascal nyelvű program newton; uses crt; var a, x, p : real; begin clrscr; write(‘Kérem az a-t: '); readln(x); write('Mi legyen a pontosság: '); readln(p); x: =1; while (abs(x-(a/x))>p) do begin x: =(x+a/x)/2; end; writeln(‘az „a” gyöke = ', x); readln; end. Ki: x Feladatok: 1. Hasonló módon határozzuk meg a négyzetgyök 5 közelítő értékét! 2. Határozzuk meg a köbgyök 2 közelítő értékét! Vissza a menühöz!