lenn klasick mechaniky 1 Klasick newtonovsk mechanika neuvauje

Členění klasické mechaniky 1 Klasická (newtonovská) mechanika – neuvažuje kvantové či relativistické efekty, platí ve standardních rozměrech (ne atomy, ne galaxie!) Členění podle zvoleného fyzikálního modelu: Ø Mechanika hmotného bodu (HB) – ignorujeme rozměry, všechna hmota je soustředěna v jednom bodě (fyzikální abstrakce - nic takového reálně neexistuje, ale někdy to tak můžeme brát…) Ø Mechanika tuhého tělesa – uvažujeme rozměry, ale síly mají jen pohybový, nikoliv deformační účinek (opět abstrakce – síla má deformační účinek, ale lze jej zanedbat) Ø Mechanika spojitých prostředí (kontinua) – zahrnuje v sobě mechaniku deformovatelných těles (uvažujeme i deformační účinky síly, zásadní význam např. ve stavitelství či strojírenství) a mechaniku tekutin (tj. kapalin a plynů)

Členění klasické mechaniky 2 Členění podle toho, čím konkrétně se zabývá: Ø Kinematika – zkoumá pohyb bez ohledu na jeho příčiny, bere „jen“ jeho časové a prostorové souvislosti (základní veličiny: dráha, rychlost, zrychlení, čas…) Ø Dynamika – zkoumá příčiny vzniku a změny pohybu (základní veličiny nad rámec kinematiky: hmotnost, síla, hybnost, moment síly či moment hybnosti) Ø Statika (ne statistika ) – zkoumá tělesa nacházející se v klidu (v určité soustavě), působící síly a rovnováhu systému

Pohyb a klid těles 1 Diskutováno již v antice Herakleitos – vše je v neustálém pohybu, „Pantha rei“ – v překladu „vše plyne“ Naopak eleaté (např. Zenon z Eleje): pohyb je jenom zdání, ve skutečnosti neexistuje Důkazy neexistence pohybu – tzv. Zenonovy pohybové aporie (Achilles a želva, Letící šíp apod. ) Později hledání absolutního pohybu či absolutního klidu (nezávislého na vztažné soustavě) – souvislost s uvažovanou existencí tzv. éteru, existovala by absolutní vztažná soustava spojená s éterem Einstein - 1905: Absolutní vztažná soustava neexistuje, pohyb a klid jsou vždy relativní pojmy!

Pohyb a klid těles 2 Vždy tedy záleží na tom, vůči čemu pohyb či klid uvažujeme (na vztažné soustavě) Každý hmotný bod či těleso je v určité soustavě v klidu (klidová soustava tělesa), v jiných se však pohybuje Příklad: Vůči soustavě spojené s učebnou jsme v klidu, vůči soustavě spojené s auty na Klatovské jsme však v pohybu, stejně tak vůči soustavě spojené se Sluncem (tam dokonce velikou rychlostí)… U většiny případů pohyb a klid vztahujeme k soustavě spojené se Zemí (např. měření rychlosti na silnici apod. je vždy vůči této soustavě!)

Základní pojmy kinematiky HB Trajektorie – křivka, kterou hmotný bod při pohybu opisuje (může to být přímka, ale i kružnice, elipsa, šroubovice, spirála či mnohé další, může být i jeden bod) Dráha – délka oblouku měřená na trajektorii, kterou hmotný bod urazí za sledovaný časový interval), skalární veličina Podle tvaru trajektorie dělíme pohyby na: Ø Přímočaré – trajektorií je část přímky Ø Křivočaré – trajektorií je jiná křivka (zvláště významný je případ kružnice)

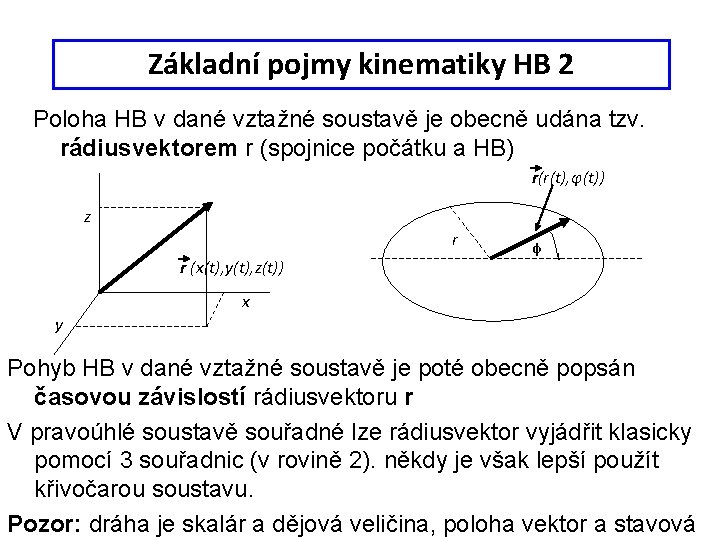
Základní pojmy kinematiky HB 2 Poloha HB v dané vztažné soustavě je obecně udána tzv. rádiusvektorem r (spojnice počátku a HB) r(r(t), φ(t)) z r r (x(t), y(t), z(t)) φ x y Pohyb HB v dané vztažné soustavě je poté obecně popsán časovou závislostí rádiusvektoru r V pravoúhlé soustavě souřadné lze rádiusvektor vyjádřit klasicky pomocí 3 souřadnic (v rovině 2). někdy je však lepší použít křivočarou soustavu. Pozor: dráha je skalár a dějová veličina, poloha vektor a stavová

Základní pojmy kinematiky HB 2 Rychlost (jednotka m*s-1), udává dráhu uraženou za čas. Nutno důsledně rozlišovat průměrnou rychlost v = s/t (skalár, podíl celkové dráhy a celkového času) a rychlost okamžitou v = ∆r/∆t, kde ∆t → 0 (vektor, uvažovaný časový interval je nekonečně malý). Matematicky je okamžitá rychlost derivací rádiusvektoru podle času, píšeme v = dr/dt !! Zrychlení (jednotka m*s-2), udává změnu rychlosti za změnu času. Opět rozlišení průměrného zrychlení a = v/t (skalár, podíl celkové změny rychlosti a celkového času) a okamžitého zrychlení a = ∆v/∆t, kde ∆t → 0 (vektor, uvažovaný časový interval je nekonečně malý). Matematicky je okamžité zrychlení derivací rychlosti podle času, píšeme a = dv/dt a zároveň 2. derivací rádiusvektoru podle času, píšeme a = d 2 r/dt 2

Kinematika HB – speciální případy Protože neumíme vyšší matematiku, musíme se pro případ pohybu po přímce omezit na dva typy pohybu: - pohyb rovnoměrný přímočarý (nulové zrychlení, stálá rychlost, s = v*t, viz ZŠ) - pohyb rovnoměrně zrychlený (či zpomalený) přímočarý - novinka, zrychlení (tj. časová změna rychlosti) je konstantní Vyšší matematika by nám umožnila pracovat s zcela obecnými pohyby hmotného bodu, dovoluje nám počítat časové závislosti dráhy, rychlosti, zrychlení, ale i určovat trajektorie různých pohybů!

Pohyb rovnoměrný přímočarý Platí pro něj, že a = 0, v = v 0 = konst. a s = v 0*t. Závislosti jednotlivých veličin na čase můžeme znázornit graficky: v (m*s-1) v 0 a (m*s-2) s (m) s =v 0*t tgφ = s/t = v 0 φ t(s) Z obrázků je vidět, že dráhu lze určit v grafu v(t) jako obsah plochy pod křivkou, rychlost v grafu s(t) poté jako směrnici tečny. To platí obecně pro jakýkoliv přímočarý pohyb!

Základní ZŠ (SŠ) úlohy 1. První auto jede z místa A rychlostí v 1. Druhé auto vyrazí za ním se zpožděním ∆t větší rychlostí v 2. Kdy a kde se potkají? Možno řešit různě, klasický postup: s 1 = s 2 v 1*t 1 = v 2*t 2 v 1*t 1 = v 2*(t 1 - ∆t) v 2*∆t = t 1* (v 2 -v 1) t 1 = v 2*∆t /(v 2 -v 1). s = v 1*t 1. 2. První auto jede z místa A rychlostí v 1. Druhé auto vyrazí z místa B vzdáleného s se zpožděním ∆t rychlostí v 2. Kdy a kde se potkají? Klasický postup: s = s 1 + s 2 s = v 1*t 1 + v 2*t 2 s = v 1*t 1 + v 2*(t 1 - ∆t) s + v 2*∆t = t 1* (v 2 + v 1) t 1 = (s + v 2*∆t) /(v 2 + v 1). s 1 = v 1*t 1.

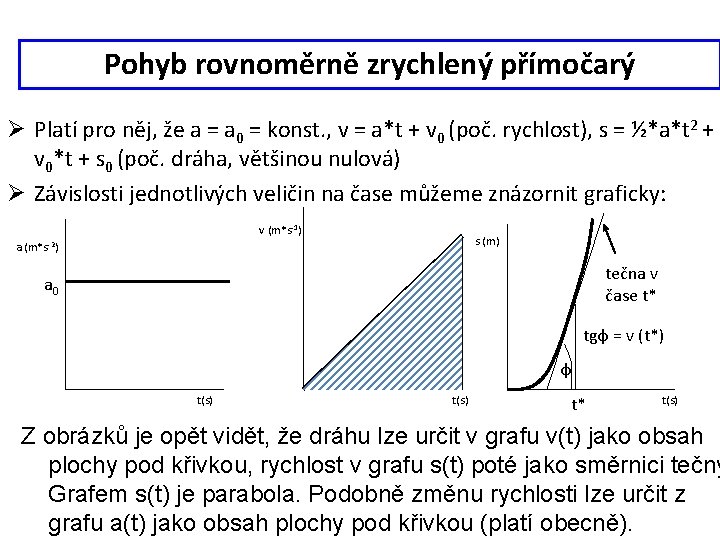
Pohyb rovnoměrně zrychlený přímočarý Ø Platí pro něj, že a = a 0 = konst. , v = a*t + v 0 (poč. rychlost), s = ½*a*t 2 + v 0*t + s 0 (poč. dráha, většinou nulová) Ø Závislosti jednotlivých veličin na čase můžeme znázornit graficky: v (m*s-1) s (m) a (m*s-2) tečna v čase t* a 0 tgφ = v (t*) s =1/2*a*t 2 t(s) φ t(s) t* t(s) Z obrázků je opět vidět, že dráhu lze určit v grafu v(t) jako obsah plochy pod křivkou, rychlost v grafu s(t) poté jako směrnici tečny Grafem s(t) je parabola. Podobně změnu rychlosti lze určit z grafu a(t) jako obsah plochy pod křivkou (platí obecně).

Pohyb rovnoměrně zrychlený Díky uvedené závislosti dráhy na čase můžeme při pohybu rov. zrychleném (či zpomaleném, což je totéž se záporným zrychlením) použít tzv. metodu průměrování. Pro uraženou dráhu pak platí jednoduchý vzoreček s = vp*t, kde vp je průměrná rychlost v době pohybu, pro kterou platí vp = (v 0 + vk)/2, kde v 0 je počáteční a vk koncová rychlost. Pro rozjezd z klidu rovnou platí vp = vk/2. Příklad 1: Letadlo se zvedlo po 675 m z rozjezdové plochy. Jaké bylo jeho konstantní zrychlení, jestliže opustilo zemi za 15 s po startu? Jakou mělo rychlost v okamžiku, kdy se vzneslo? Řešení: Rovnoměrně zr. pohyb s nulovou poč. rychlostí s = vp*t vp = s/t = 675/15 = 45 m/s. vp = vk/2 vk = 2* vp = 2*45 = 90 m/s. Pro zrychlení: a = ∆v/∆t = 90/15 = 6 m/s 2. Příklad 2: Auto snížilo během 5 s rovnoměrně svoji rychlost z 25 m/s na 15 m/s. Jakou dráhu přitom urazilo? Řešení: Rovnoměrně zpom. pohyb s nenulovou poč. rychlostí vp = (v 0 + vk)/2 = (15 + 25) / 2 = 20 m/s. s = vp*t = 20*5 = 100 m.

Pohyb nerovnoměrný přímočarý Platí pro něj, že a není konstantní, v i s se poté musí určit pomocí integrálů Závislosti jednotlivých veličin na čase mohou vypadat třeba takto: v (m*s-1) v 0 a (m*s-2) s (m) tečna v čase t* a 0 tgφ = v (t*) φ t(s) t* t(s) Grafy jsou složité, opět však lze dráhu lze určit v grafu v(t) jako obsah plochy pod křivkou, rychlost v grafu s(t) poté jako směrnici tečny. Změnu rychlosti lze z grafu a(t) určit jako obsah plochy pod křivkou.

Příklad – rovnoměrně zrychlený pohyb Zadání: Těleso se pohybuje rovnoměrně zrychleně s počáteční rychlostí v 0 = 3 m*s-1 a zrychlením a = 2 m*s-2. Určete dráhu uraženou během prvních deseti sekund pohybu a konečnou rychlost. Řešení: Dosazením t = 10 s do vztahů pro rovnoměrně zrychlený pohyb okamžitě dostáváme: vk = v 0+a*t = 3 + 2*10 = 23 m*s-1 s(10) = ½*a*t 2+v 0*t+s 0 = ½*2*102+3*10+0 = 130 m (případně vp = (v 0 + vk)/2 = (3 + 23)/2 = 13 m/s; s (10) = vp*t = 13*10 = 130 m).