Lecture 6 RSA Use in Encryption to encrypt

Lecture 6

RSA Use in Encryption • to encrypt a message M the sender: – obtains public key of recipient PU={e, n} – computes: C = Me mod n, where 0≤M<n • to decrypt the ciphertext C the owner: – uses their private key PR={d, n} – computes: M = Cd mod n • note that the message M must be smaller than the modulus n (block if needed)

RSA Example - En/Decryption • sample RSA encryption/decryption is: • given message M = 88 1. Publish public key PU={7, 187} 2. Keep secret private key PR={23, 187} • encryption: C = 887 mod 187 = 11 • decryption: M = 1123 mod 187 = 88

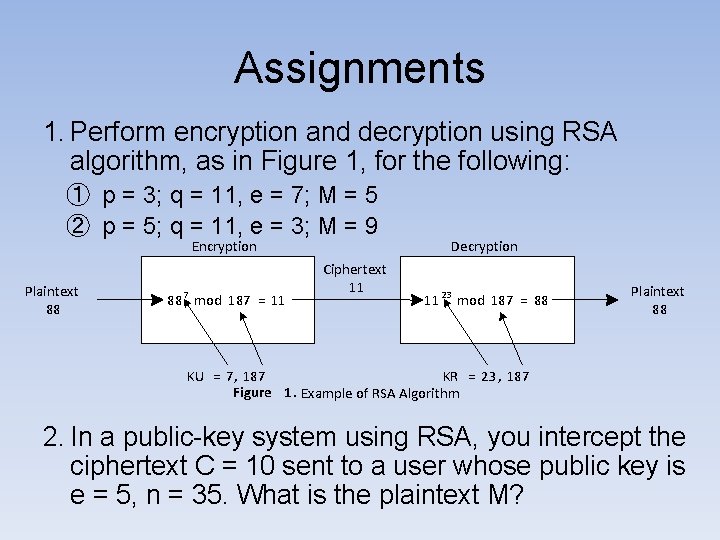
Assignments 1. Perform encryption and decryption using RSA algorithm, as in Figure 1, for the following: ① p = 3; q = 11, e = 7; M = 5 ② p = 5; q = 11, e = 3; M = 9 Encryption Plaintext 88 88 7 mod 187 = 11 Ciphertext 11 Decryption 11 23 mod 187 = 88 Plaintext 88 KU = 7, 187 KR = 23 , 187 Figure 1. Example of RSA Algorithm 2. In a public-key system using RSA, you intercept the ciphertext C = 10 sent to a user whose public key is e = 5, n = 35. What is the plaintext M?

Why RSA Works • because of Euler's Theorem: – aø(n)mod n = 1 where gcd(a, n)=1 • in RSA have: – – n=p. q ø(n)=(p-1)(q-1) carefully chose e & d to be inverses mod ø(n) hence e. d=1+k. ø(n) for some k • hence : Cd = Me. d = M 1+k. ø(n) = M 1. (Mø(n))k = M 1. (1)k = M 1 = M mod n

Efficient Encryption • Encryption uses exponentiation to power e • Hence if e small, this will be faster – often choose e=65537 (216 -1) – also see choices of e=3 or e=17 • But if e too small (eg e=3) can attack – using Chinese remainder theorem & 3 messages with different moduli

Efficient Decryption • Decryption uses exponentiation to power d – this is likely large, insecure if not • can use the Chinese Remainder Theorem (CRT) to compute mod p & q separately. then combine to get desired answer

Exponentiation • • can use the Square and Multiply Algorithm a fast, efficient algorithm for exponentiation concept is based on repeatedly squaring base and multiplying in the ones that are needed to compute the result • look at binary representation of exponent • only takes O(log 2 n) multiples for number n – eg. 75 = 74. 71 = 3. 7 = 10 mod 11 – eg. 3129 = 3128. 31 = 5. 3 = 4 mod 11

Exponentiation • The algorithm for computing ab mod n • The b integer is expressed as as binary number : bk , bk-1 , …, b 0

Example • Get 7 5 mod 11= ? ? ab mod n as in th algorithm 1 0 1 b 2 b 1 b 0 • So b= 5 101 k Ask? b(k) • n= 11 a= 7 • The final result is = 10 c 0 2 0 Yes b 2 = 1 1 1 d 1 1 7 2 5 No 0 4 3 5 10

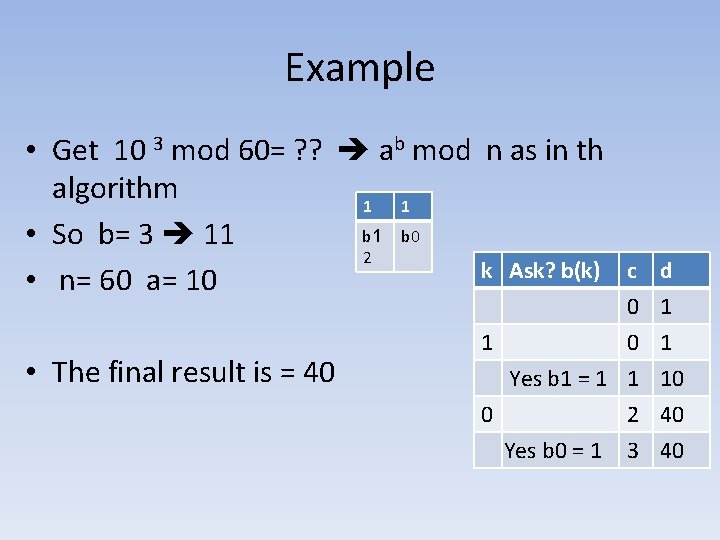
Example • Get 10 3 mod 60= ? ? ab mod n as in th algorithm 1 1 b 0 • So b= 3 11 2 k Ask? b(k) • n= 60 a= 10 • The final result is = 40 c 0 1 0 Yes b 1 = 1 1 0 Yes b 0 = 1 d 1 1 10 2 40 3 40

RSA Security • three approaches to attacking RSA: – brute force key search (infeasible given size of numbers) – mathematical attacks (based on difficulty of computing ø(N), by factoring modulus N) – timing attacks (on running of decryption)

Factoring Problem • mathematical approach takes 3 forms: – factor N=p. q, hence find ø(N) and then d – determine ø(N) directly and find d – find d directly • currently believe all equivalent to factoring – have seen slow improvements over the years • as of Aug-99 best is 130 decimal digits (512) bit with GNFS – biggest improvement comes from improved algorithm • cf “Quadratic Sieve” to “Generalized Number Field Sieve” – barring dramatic breakthrough 1024+ bit RSA secure • ensure p, q of similar size and matching other constraints

Summary • have considered: – prime numbers – Fermat’s and Euler’s Theorems – Primality Testing – Chinese Remainder Theorem – Discrete Logarithms – principles of public-key cryptography – RSA algorithm, implementation, security