Lecture 5 Measurement and Scaling Fundamentals and Comparative

Lecture 5 Measurement and Scaling: Fundamentals and Comparative Scaling

8 -2 Measurement and Scaling Measurement means assigning numbers or other symbols to characteristics of objects according to certain prespecified rules. n One-to-one correspondence between the numbers and the characteristics being measured. n The rules for assigning numbers should be standardized and applied uniformly. n Rules must not change over objects or time.

8 -3 Measurement and Scaling involves creating a continuum upon which measured objects are located. Example: Consider a scale measuring attitude of customers toward department stores. Each respondent is assigned a number from 1 to 100, with 1 = Extremely Unfavorable, and 100 = Extremely Favorable. Measurement is the actual assignment of a number from 1 to 100 to each respondent. Scaling is the process of placing the respondents on a continuum with respect to their attitude toward department stores.

8 -4 Primary Scales of Measurement Scale Nominal Ordinal Symbols Assigned to Runners Finish B Ratio G Finish Rank Order of Winners 3 rd place Interval S Performance Rating on a 8. 2 0 to 10 Scale Time to 15. 2 Finish, in Seconds 2 nd place 1 st place 9. 1 9. 6 14. 1 13. 4

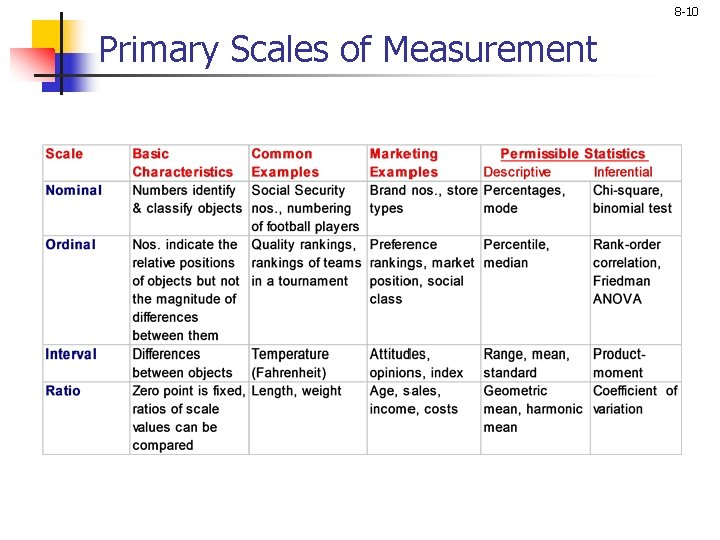
Primary Scales of Measurement 8 -5 Nominal Scale n n n The numbers serve only as labels or tags for identifying and classifying objects. When used for identification, there is a strict one-toone correspondence between the numbers and the objects. The numbers do not reflect the amount of the characteristic possessed by the objects. The only permissible operation on the numbers in a nominal scale is counting. Only a limited number of statistics, all of which are based on frequency counts, are permissible, e. g. , percentages, and mode.

Primary Scales of Measurement 8 -6 Ordinal Scale n n A ranking scale in which numbers are assigned to objects to indicate the relative extent to which the objects possess some characteristic. Can determine whether an object has more or less of a characteristic than some other object, but not how much more or less. Any series of numbers can be assigned that preserves the ordered relationships between the objects. In addition to the counting operation allowable for nominal scale data, ordinal scales permit the use of statistics based on centiles, e. g. , percentile, quartile, median.

Primary Scales of Measurement 8 -7 Interval Scale n n n Numerically equal distances on the scale represent equal values in the characteristic being measured. It permits comparison of the differences between objects. For example, the difference between 1 and 2 is the same as between 3 and 4. The difference between 1 and 9 (i. e. , 8) is twice as large as the difference between 2 and 4 (i. e. , 2) or 6 and 8 (2). The location of the zero point is not fixed. Both the zero point and the units of measurem. are arbitrary. It is NOT meaningful to take ratios of scale values It IS meaningful to take ratios of their differences. Statistical techniques that may be used include all of those that can be applied to nominal and ordinal data, and in addition the arithmetic mean, standard deviation, correlation, and other common statistics.

Primary Scales of Measurement 8 -8 Ratio Scale n n n Possesses all the properties of the nominal, ordinal, and interval scales. It has an absolute zero point. Examples: height, weight, age, money, sales, costs, market share, number of customers, the rate of return. It is meaningful to compute ratios of scale values. For example, not only is the difference between 2 and 5 the same as the difference between 14 and 17, but also 14 is seven times as large as 2 in an absolute sense. All statistical techniques can be applied to ratio data.

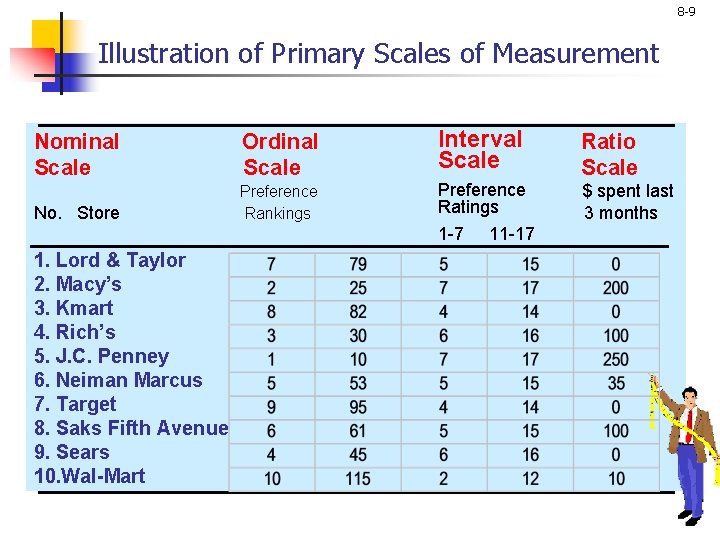
8 -9 Illustration of Primary Scales of Measurement Nominal Scale Ordinal Scale Interval Scale Ratio Scale No. Store Preference Rankings Preference Ratings 1 -7 11 -17 $ spent last 3 months 1. Lord & Taylor 2. Macy’s 3. Kmart 4. Rich’s 5. J. C. Penney 6. Neiman Marcus 7. Target 8. Saks Fifth Avenue 9. Sears 10. Wal-Mart

8 -10 Primary Scales of Measurement

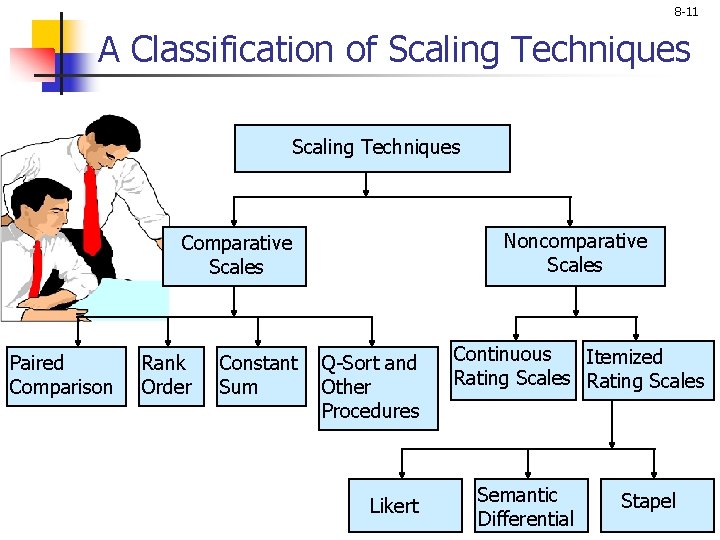
8 -11 A Classification of Scaling Techniques Noncomparative Scales Comparative Scales Paired Comparison Rank Order Constant Q-Sort and Sum Other Procedures Likert Continuous Itemized Rating Scales Semantic Differential Stapel

8 -12 A Comparison of Scaling Techniques n Comparative scales involve the direct comparison of stimulus objects. Comparative scale data must be interpreted in relative terms and have only ordinal or rank order properties. n In noncomparative scales, each object is scaled independently of the others in the stimulus set. The resulting data are generally assumed to be interval or ratio scaled.

8 -13 Relative Advantages of Comparative Scales n n n Small differences between stimulus objects can be detected (respondents are forced to choose between two objects). Same known reference points for all respondents. Easily understood and can be applied easily. Involve fewer theoretical assumptions. Tend to reduce halo or carryover effects from one judgment to another (e. g. , comparing Pepsi vs. Coke will not influence comparing Sprite vs. 7 -up).

8 -14 Relative Disadvantages of Comparative Scales n n Ordinal nature of the data: only limited number of statistical techniques can be used Inability to generalize beyond the objects scaled (i. e. , if Coke and Pepsi are compared, we do not know how Sprite would be evaluated by the respondent. Another study is needed: Coke vs. Sprite, and Pepsi vs. Sprite)

Comparative Scaling Techniques 8 -15 Paired Comparison Scaling n n n A respondent is presented with two objects and asked to select one according to some criterion. The data obtained are ordinal in nature. Paired comparison scaling is the most widely used comparative scaling technique. With n brands, [n(n - 1) /2] paired comparisons are required (no good when n is large) Under the assumption of transitivity (if A is better than B, and B is better than C, then A is better than C), it is possible to convert paired comparison data to a rank order. Does not match real life well: consumers face multiple choices rather than two at a time.

Obtaining Shampoo Preferences Using Paired Comparisons 8 -16 Instructions: We are going to present you with ten pairs of shampoo brands. For each pair, please indicate which one of the two brands of shampoo you would prefer for personal use. Recording Form: a. A 1 in a particular box means that the brand in that column was preferred over the brand in the corresponding row. A 0 means that the row brand was preferred over the column brand. b. The number of times a brand was preferred is obtained by summing the 1 s in each column.

8 -17 Paired Comparison Selling The most common method of taste testing is paired comparison. The consumer is asked to sample two different products and select the one with the most appealing taste. The test is done in private and a minimum of 1, 000 responses is considered an adequate sample. Coca. Cola is reported to have conducted more than 190, 000 paired comparisons before introducing New Coke. A paired comparison (blind) taste test

Comparative Scaling Techniques 8 -18 Rank Order Scaling n n n Respondents are presented with several objects simultaneously and asked to order or rank them according to some criterion. It is possible that the respondent may dislike the brand ranked 1 in an absolute sense. Furthermore, rank order scaling also results in ordinal data. Only (n - 1) scaling decisions need be made in rank order scaling. Better resembles real life shopping (multiple choices)

Preference for Toothpaste Brands Using Rank Order Scaling Instructions: Rank the various brands of toothpaste in order of preference. Begin by picking out the one brand that you like most and assign it a number 1. Then find the second most preferred brand assign it a number 2. Continue this procedure until you have ranked all the brands of toothpaste in order of preference. The least preferred brand should be assigned a rank of 10. No two brands should receive the same rank number. The criterion of preference is entirely up to you. There is no right or wrong answer. Just try to be consistent. 8 -19

Preference for Toothpaste Brands Using Rank Order Scaling Form Brand Rank Order 1. Crest _____ 2. Colgate _____ 3. Aim _____ 4. Gleem _____ 5. Macleans _____ 6. Ultra Brite _____ 7. Close Up _____ 8. Pepsodent _____ 9. Plus White _____ 10. Stripe _____ 8 -20

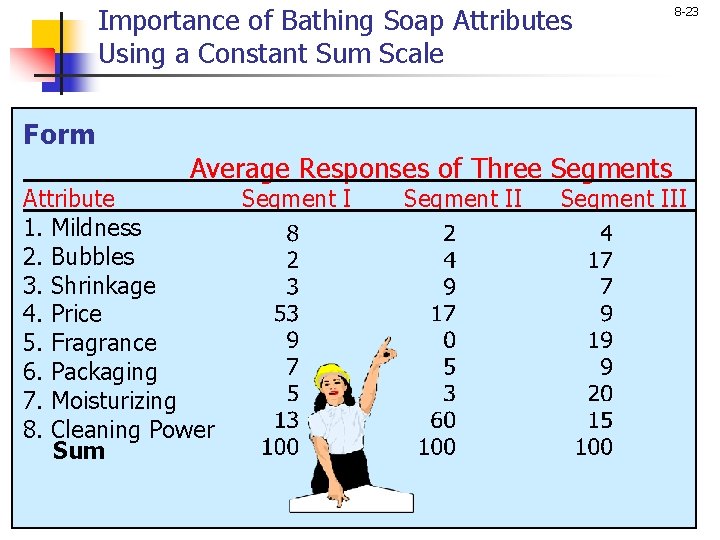
Comparative Scaling Techniques 8 -21 Constant Sum Scaling n n Respondents allocate a constant sum of units, such as 100 points to attributes of a product to reflect their importance. If an attribute is unimportant, the respondent assigns it zero points. If an attribute is twice as important as some other attribute, it receives twice as many points. The sum of all the points is 100. Hence, the name of the scale.

Importance of Bathing Soap Attributes Using a Constant Sum Scale Instructions On the next slide, there are eight attributes of bathing soaps. Please allocate 100 points among the attributes so that your allocation reflects the relative importance you attach to each attribute. The more points an attribute receives, the more important the attribute is. If an attribute is not at all important, assign it zero points. If an attribute is twice as important as some other attribute, it should receive twice as many points. 8 -22

Importance of Bathing Soap Attributes Using a Constant Sum Scale 8 -23 Form Average Responses of Three Segments Attribute Segment III 1. Mildness 2. Bubbles 3. Shrinkage 4. Price 5. Fragrance 6. Packaging 7. Moisturizing 8. Cleaning Power Sum