L ELLISSE 1 ARGOMENTI TRATTATI 1 Lequazione canonica
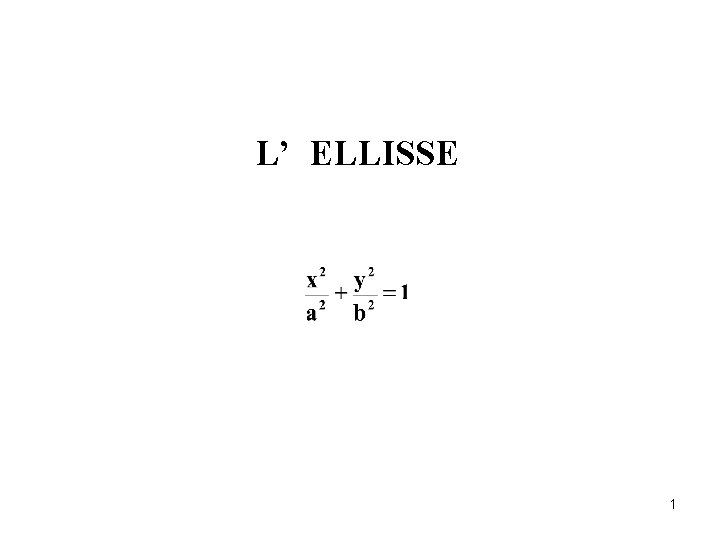
















- Slides: 22
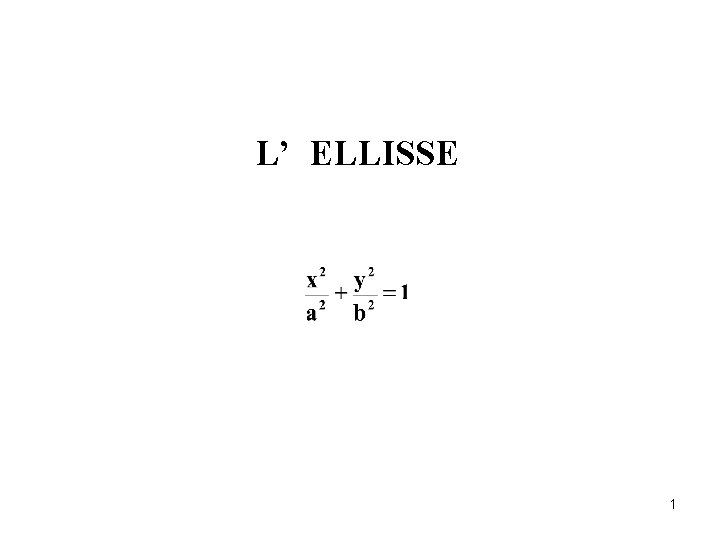
L’ ELLISSE 1

ARGOMENTI TRATTATI 1. L’equazione canonica dell’ellisse 2. Questioni basilari 3. Questioni relative alle rette tangenti 4. Curve deducibili dall’ellisse 5. Discussione di sistemi di 2° grado con parametro 6. Proprietà ottica dell’ellisse 2

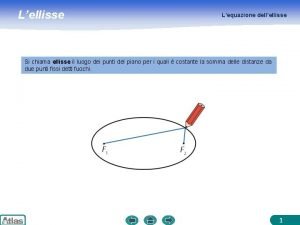
L’EQUAZIONE CANONICA DELL’ELLISSE Definizione Si dice elisse E il luogo geometrico dei punti P del piano tali che sia costante la somma delle distanze di P da due punti distinti F 1 ed F 2, detti fuochi. Da questa definizione, ponendoci in un opportuno riferimento cartesiano, possiamo ricavare l’equazione canonica dell’ellisse. Siano F 1(- c ; 0 ) e F 2(c ; 0 ), con c reale positivo, i fuochi e P(x; y) un generico punto P della E. Tali punti devono soddisfare la condizione dettata dalla definizione, cioè: 3

4

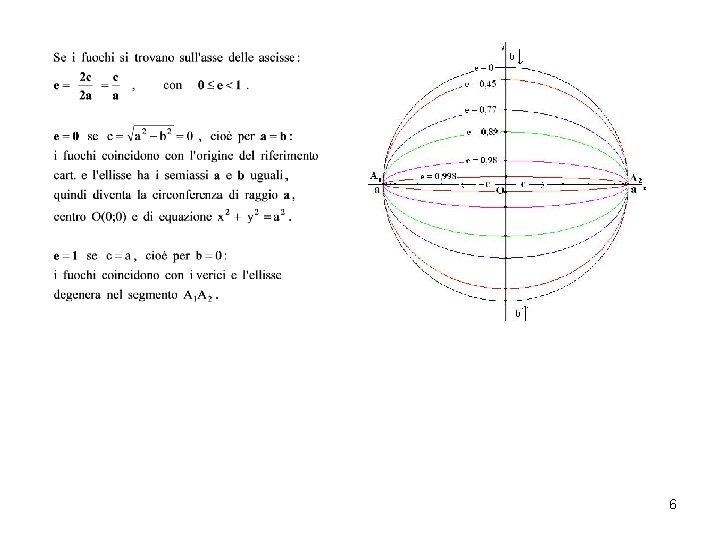
Osservazioni e altre definizioni (fuochi sull’asse x) a. Gli insiemi d’appartenenza di x e y e le coordinate dei vertici suggeriscono che l’ellisse è inscritta nel rettangolo di figura, avente i lati lunghi 2 a e 2 b e i vertici di coordinate (-a; -b); (a; b); (-a; b). b. I segmenti A 1 A 2 e B 1 B 2 si chiamano rispettivamente asse maggiore, di misura 2 a, e asse minore, di misura 2 b ( ricordiamo che b < a ); il segmento F 1 F 2 si chiama distanza focale e misura 2 c. Simmetrie nell’ellisse con equazione canonica: F(-x; -y) = F(x; y), quindi l’ellisse è una curva a simmetria centrale, con centro O(0; 0); F(-x; y) = F(x; y), quindi l’ellisse è una curva a simmetria assiale, con asse di simm. l’asse delle y ; F(x; -y) = F(x; y), quindi l’ellisse è una curva a simmetria assiale, con asse di simm. l’asse delle x. d. Considerazione sul grafico per ricordare la relazione a 2 – c 2 = b 2 oppure c 2 = a 2 – b 2 : se consideriamo il punto P, che descrive la curva, nel vertice B 2, si forma il triangolo rettangolo OF 2 B 2 di ipotenusa a e cateti b e c, quindi … e. Coordinate dei fuochi di un’ellisse di equazione nota: se sono noti a e b, allora e i fuochi hanno coordinate F 1(-c ; 0), F 2(c ; 0). f. Eccentricità ‘e’. Il rapporto fra la distanza focale e la lunghezza dell’asse maggiore di un’ellisse è detto eccentricità: 5

6

L’ellisse con i fuochi appartenenti all’asse y Dalla definizione di ellisse come luogo geometrico (pag. 3), procedendo come nel caso dell’ellisse con i fuochi sull’asse delle x, si ottiene la stessa equazione canonica. Siano F 1(0 ; - c) e F 2(0 ; c), con c reale positivo, i fuochi e P(x; y) un generico punto P della E. Tali punti devono soddisfare la condizione dettata dalla definizione, cioè: 7

Osservazioni e altre definizioni (fuochi sull’ asse y) a. Gli insiemi d’appartenenza di x e y … invariati b. I segmenti A 1 A 2 e B 1 B 2 si chiamano rispettivamente asse minore, di misura 2 a, e asse maggiore, di misura 2 b ( ricordiamo che b > a ); il segmento F 1 F 2 si chiama distanza focale e misura 2 c. Simmetrie … invariate d. Considerazione sul grafico per ricordare la relazione b 2 – c 2 = a 2 oppure c 2 = b 2 – a 2 : se consideriamo il punto P, che descrive la curva, nel vertice A 2, si forma il triangolo rettangolo OF 2 A 2 di ipotenusa b e cateti a e c, quindi … e. Coordinate dei fuochi di un’ellisse di equazione nota: se sono noti a e b, allora e i fuochi hanno coordinate F 1(0 ; -c), F 2(0 ; c). f. Eccentricità ‘e’. Il rapporto fra la distanza focale e la lunghezza dell’asse maggiore di un’ellisse è detto eccentricità: 8

QUESTIONI BASILARI 1. Date le seguenti equazioni canoniche di ellissi, traccia i grafici corrispondenti, dopo aver determinato le coordinate dei vertici e dei fuochi, la misura degli assi maggiore e minore, l’eccentricità. 9

2. Determina per quali valori del parametro reale k l’equazione rappresenta un’ellisse. kx 2 + (k + 3)y 2 = k + 15 3. Determina per quali valori del parametro reale k l’equazione rappresenta un’ellisse con i fuochi sull’asse delle ascisse. (3 - k)x 2 + (k + 2)y 2 = - k 2 + k + 6 10

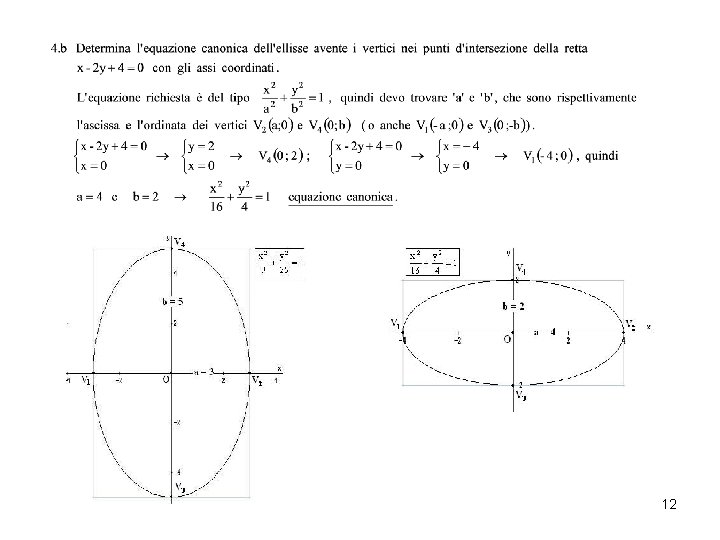
4. PROBLEMA RICORRENTE: determinare l’equazione di un’ellisse. Facendo riferimento all’equazione canonica, determinare l’equazione di un’ellisse significa determinare i due coefficienti a, b. Pertanto il problema deve fornire due condizioni tra loro indipendenti, da cui ricavare due equazioni indipendenti. Alcune di tali condizioni sono, per esempio: • • • conosco a e/o b (coordinate dei vertici o lunghezze dei semiassi) conosco c (coordinate di un fuoco) passaggio per un dato punto P(xp ; yp) (xp)2 /a 2 + (yp)2 / b 2 = 1 conosco l’eccentricità e = c/a o e = c/b tangenza ad una retta di nota equazione y = mx +q vedi Ellisse tangente ad una retta. 11

12

QUESTIONI RELATIVE ALLE RETTE TANGENTI Analizziamo questi due problemi: 1. 2. determinare le equazioni delle rette tangenti all’ellisse, condotte da un punto di note coordinate; determinare l’equazione dell’ellisse tangente ad una retta di nota equazione. 1. Rette tangenti all’ellisse, condotte da un punto P Questi problemi si possono trattare, come indicato nel capitolo 9 delle coniche, con il metodo del discriminante nullo, o con il metodo delle formule di sdoppiamento. Di solito conviene applicare il metodo delle formule di sdoppiamento se il punto P appartiene all’ellisse. 2. Esempi a. Determina le equazioni delle rette tangenti all’ellisse di equaz. x 2 + 4 y 2 = 4 , condotte dal punto P(3 ; 0). Verifico se P appartiene all’ellisse: 9 4 P non appartiene all’ellisse, quindi posso avere due soluzioni, se P è esterno, nessuna soluzione, se P è interno all’ellisse. Metodo del “discriminante nullo” 13

b. Determina le equazioni delle rette tangenti all’ellisse 16 x 2 + 25 y 2 = 4 , condotte dal punto P(1/4 ; 31/2/5). Verifico se P appartiene all’ellisse: 1+ 3 = 4 P appartiene all’ellisse, quindi ho una soluzione. 14

2. Ellisse tangente ad una retta di nota equazione Esempio 15

CURVE DEDUCIBILI DALL’ ELLISSE Esplicitando l’equazione di secondo grado x 2/a 2 + y 2/b 2 = 1 rispetto alla variabile y e rispetto alla variabile x , si ottengono quattro equazioni, due del tipo (1) e due del tipo (2), scritte sotto. Tali equazioni sono rappresentate graficamente da semiellissi. 16

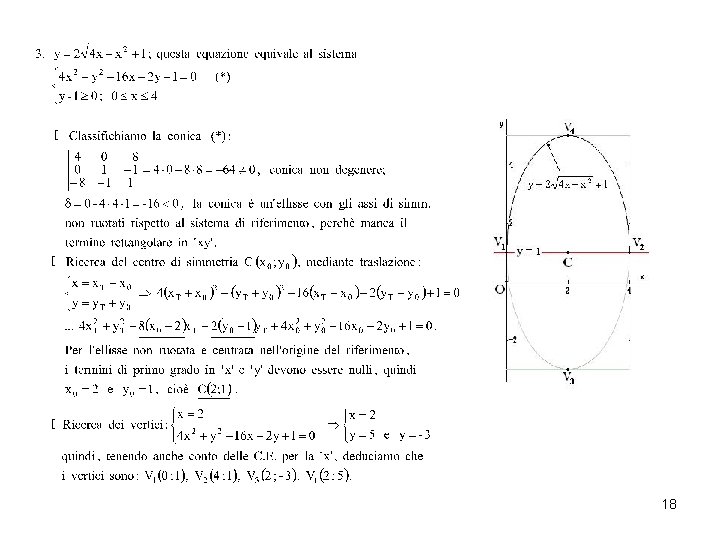
Esempi. Rappresenta graficamente le curve descritte dalle equazioni indicate. 17

18

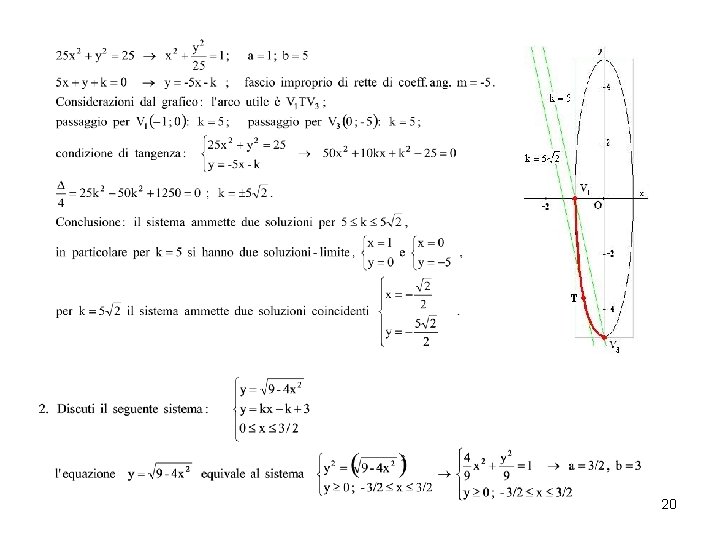
DISCUSSIONE DI SISTEMI DI 2° GRADO CON PARAMETRO CASO ELLISSE – RETTA Il parametro del sistema è il parametro che caratterizza il fascio di rette o di circonferenze. Discutere un sistema del tipo (1) o (2), significa determinare, compatibilmente alle eventuali limitazioni, per quali valori del parametro le rette intersecano l’ellisse nel caso (1), o la retta interseca le ellissi nel caso (2). In questo contesto ci occuperemo solo del caso (1). Esempi 19

20

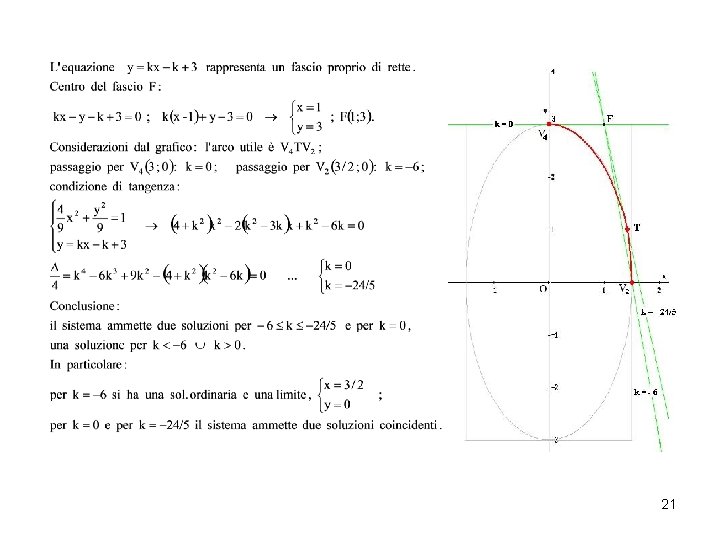
21

PROPRIETA’ OTTICA DELL’ELLISSE Un raggio di luce proveniente da uno dei due fuochi viene riflesso dall’ellisse verso l’altro fuoco. Questa proprietà, che si può facilmente dimostrare per via analitica, vale per tutti i tipi di onde, anche per quelle acustiche. Si può ricordare un fenomeno acustico, che è possibile sperimentare in antiche sale con il soffitto a sezione ellittica, dove due interlocutori, posti nei due fuochi, possono discorrere chiaramente, sebbene a voce bassa, mentre negli altri punti della sala non si sentono le loro parole. Questa proprietà è stata sfruttata nella costruzione di alcuni teatri rinascimentali. 22
 Trattati localizzabili
Trattati localizzabili Coordinate polari ellisse
Coordinate polari ellisse Stefano lagomarsino
Stefano lagomarsino Considera l'ellisse rappresentata in figura
Considera l'ellisse rappresentata in figura Equazione ellisse
Equazione ellisse Ecuación canónica ejercicios resueltos
Ecuación canónica ejercicios resueltos Base canonica polinomio grado 2
Base canonica polinomio grado 2 Ecuacion canonica de la circunferencia con centro h k
Ecuacion canonica de la circunferencia con centro h k Posicion canonica
Posicion canonica Informazione booleana
Informazione booleana Prima forma canonica
Prima forma canonica La frase minima
La frase minima Indice argomenti
Indice argomenti Indice argomenti
Indice argomenti