Introduction to The Lifting Scheme Wavelet Transforms Two

Introduction to The Lifting Scheme

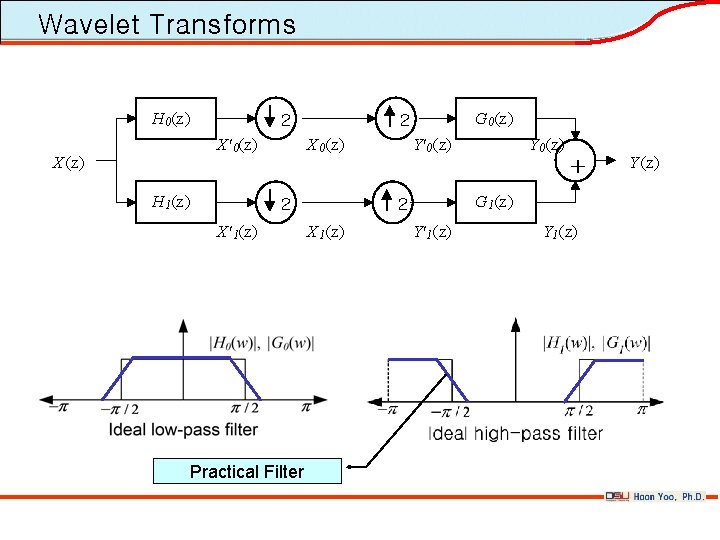
Wavelet Transforms • Two approaches to make a wavelet transform: – Scaling function and wavelets (dilation equation and wavelet equation) – Filter banks (low-pass filter and high-pass filter) • The two approaches produce same results, proved by Doubeches. • Filter bank approach is preferable in signal processing literatures

Wavelet Transforms H 0(z) 2 X' 0(z) X(z) H 1(z) X 0(z) 2 X' 1(z) Practical Filter G 0(z) 2 Y'0(z) + G 1(z) 2 X 1(z) Y 0(z) Y'1(z) Y(z)

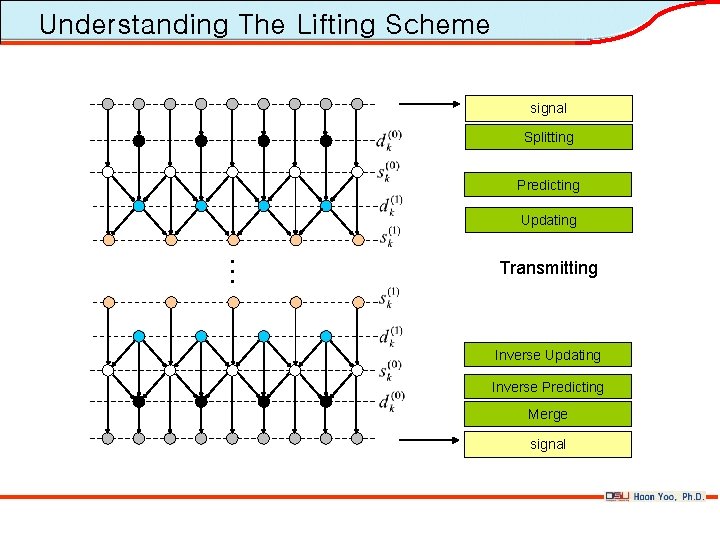
Understanding The Lifting Scheme signal Splitting Predicting Updating … Transmitting Inverse Updating Inverse Predicting Merge signal

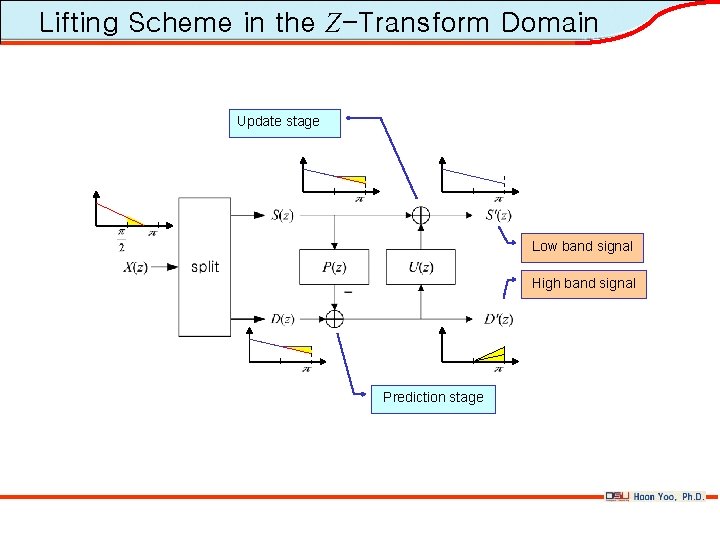
Lifting Scheme in the Z-Transform Domain Update stage Low band signal High band signal Prediction stage

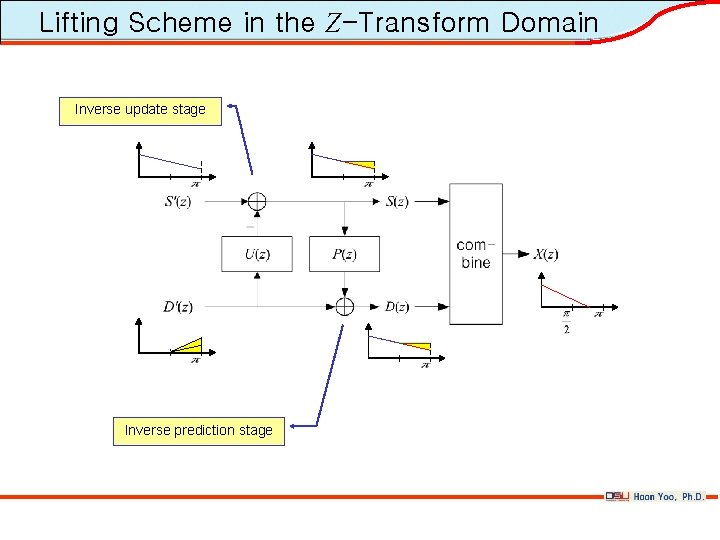
Lifting Scheme in the Z-Transform Domain Inverse update stage Inverse prediction stage

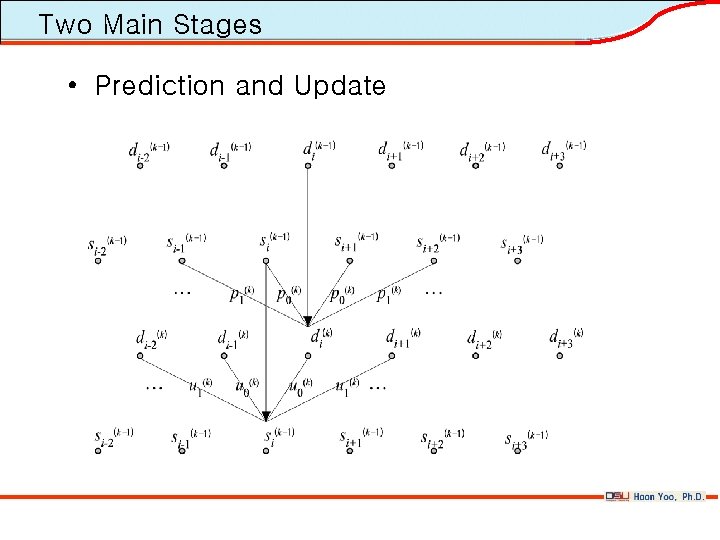
Four Basic Stages • A spatial domain construction of biorthogonal wavelets, consists of the following four basic operations: • Split : sk(0)=x 2 i(0), dk(0)=x 2 i+1(0) • Predict : dk(r)= dk(r-1) – pj(r) sk+j(r-1) • Update : sk(r)= sk(r-1) + uj(r) dk+j(r) • Normalize : sk(R)=K 0 sk(R), dk(R)=K 1 dk(R)

Two Main Stages • Prediction and Update

Prediction Stage • A prediction rule : interpolation – Linear interpolation coefficients: [1, 1]/2 • used in the 5/3 filter – Cubic interpolation coefficients: [-1, 9, 9, -1]/16 • used in the 13/7 CRF and the 13/7 SWE

Update Stage • An update rule : preservation of average (moments) of the signal – The update coefficients in the 5/3 are [1, 1]/4 – The update coefficients in the 13/7 SWE are [-1, 9, 9, -1]/32 – The update coefficients in the 13/7 CRF are [-1, 5, 5, -1]/16

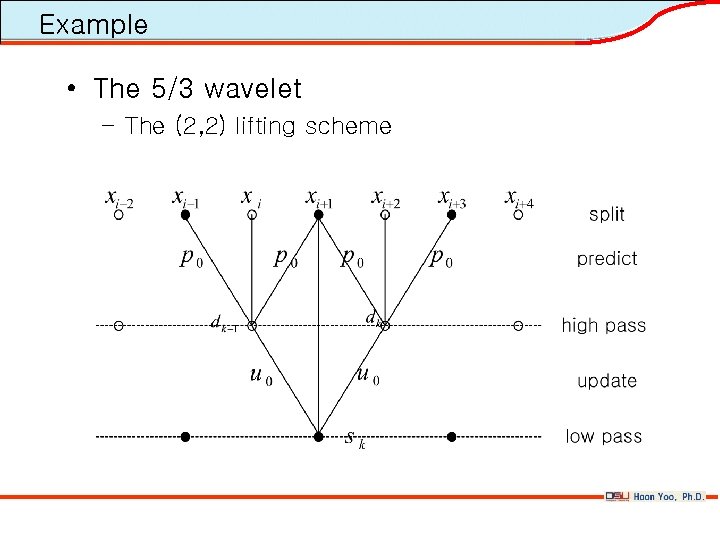
Example • The 5/3 wavelet – The (2, 2) lifting scheme

Example • We have p 0 = 1/2 by linear interpolation and the detailed coefficient are given by • In the update stage, we first assure that the average of the signal be preserved • From an update of the form, we have • From this, we get A=1/4 as the correct choice to maintain the average.

Example • The coefficients of the corresponding high pass filter are {h 1} = ½{-1, 2, -1} • The coefficients of the corresponding low pass filter are {h 0} = ⅛{-1, 2, 6, 2, -1} • So, the (2, 2) lifting scheme is equal to the 5/3 wavelet.

Example • Complexity of the lifting version and the conventional version – The conventional 5/3 filter • X_low = ( 4*x[0]+2*(x[-1]+x[1])-(x[2]+x[-2]) )/8 • X_high = x[0]-(x[1]+x[-1])/2 • Number of operations per pixel = 9+3 = 12 – The (2, 2) lifting • D[0] = x[0]- (x[1]+x[-1])/2 • S[0] = x[0] + (D[0]+D[1])/4 • Number of operations per pixel = 6

Conclusions • The lifting scheme is an alternative method of computing the wavelet coefficients • Advantages of the lifting scheme: – Requires less computation and less memory. – Easily produces integer-to-integer wavelet transforms for lossless compression. – Linear, nonlinear, and adaptive wavelet transform is feasible, and the resulting transform is invertible and reversible.