Dr Scheme Dr Scheme PLT Scheme Dr Scheme

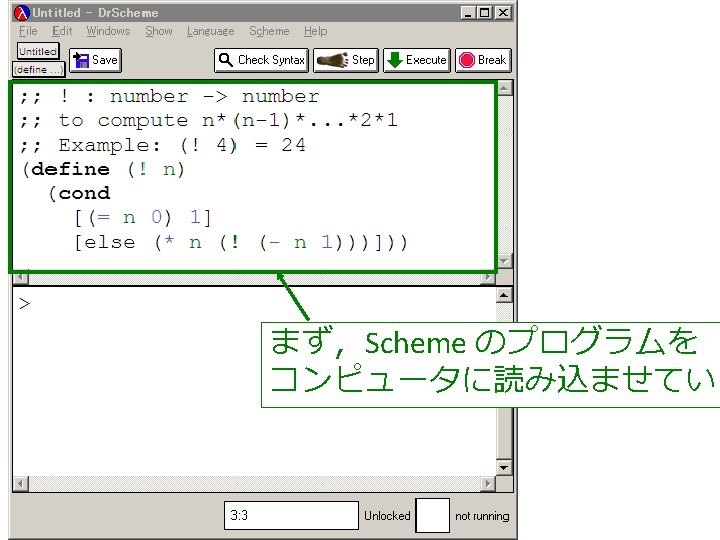
Dr. Scheme の使用 • Dr. Scheme の起動 プログラム　→ PLT Scheme → Dr. Scheme • 今日の演習では「Intermediate Student 」 に設定 Language → Choose Language → Intermediate Student

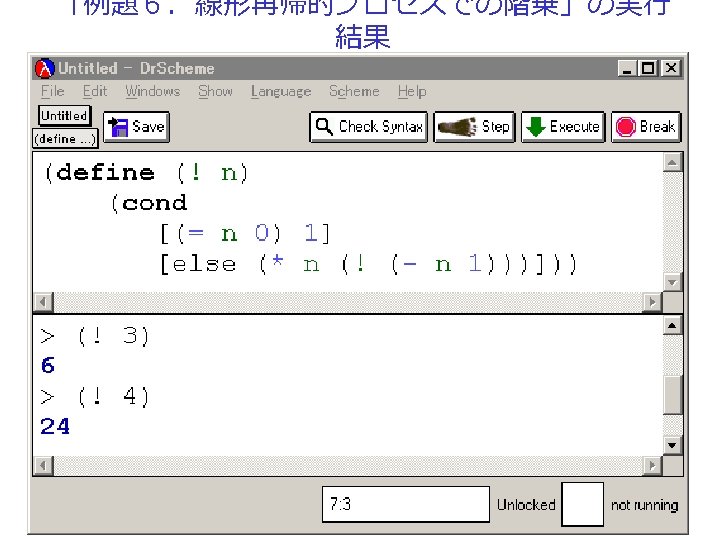
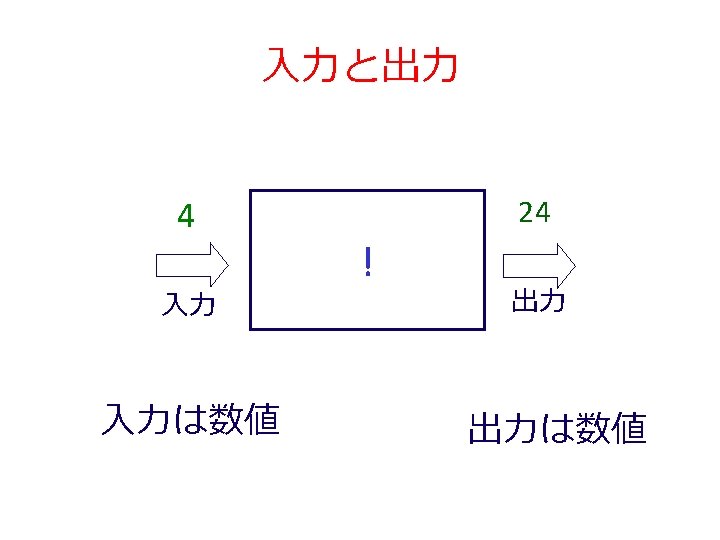
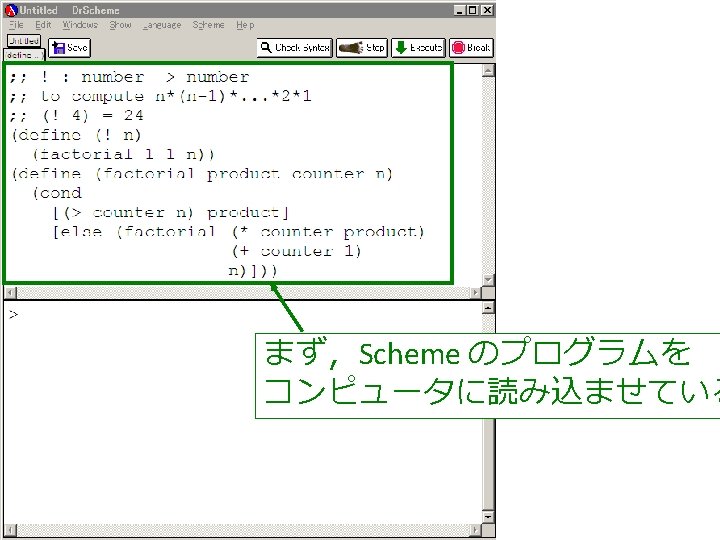
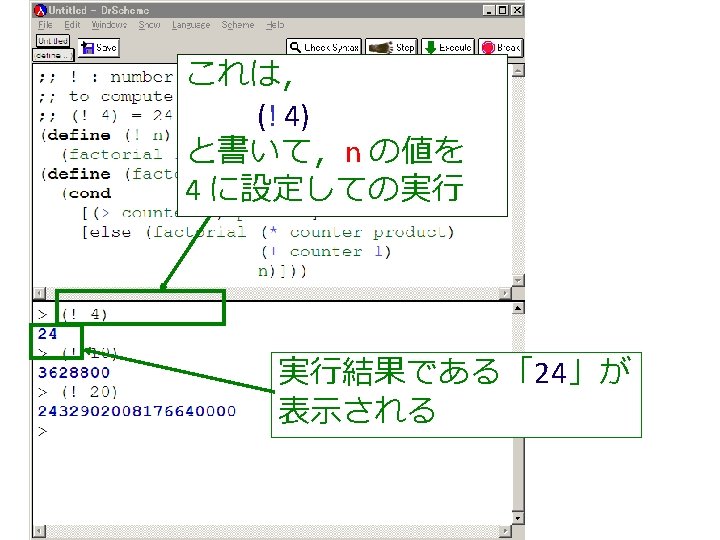
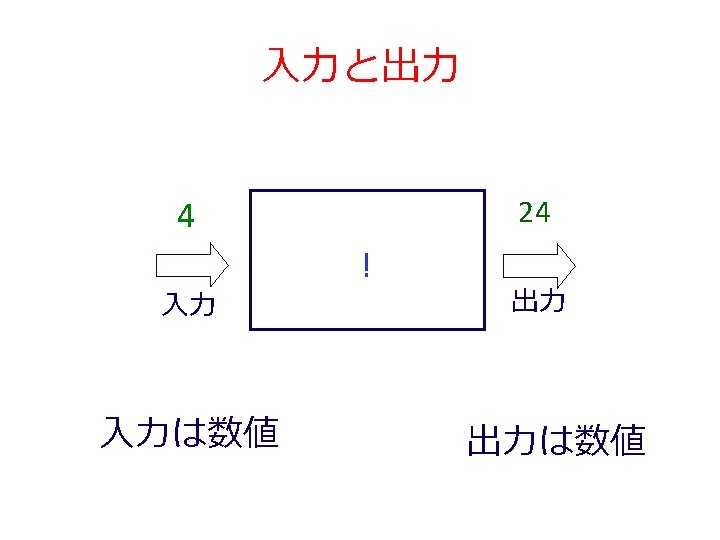
! 関数 ; ; ! : number -> number ; ; to compute n*(n-1)*. . . *2*1 ; ; (! 4) = 24 (define (! n) (factorial 1 1 n)) (define (factorial product counter n) product ← counter・produc (cond [(> counter n) product] [else (factorial (* counter product) (+ counter 1) n)])) counter ← counter + 1

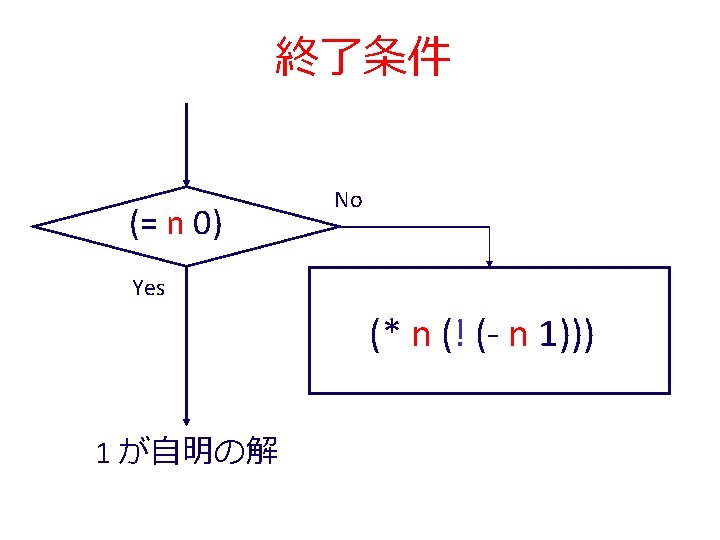
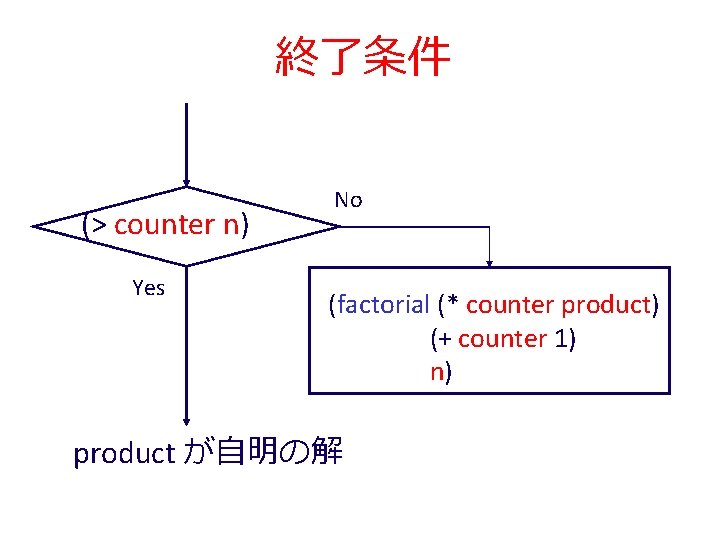
反復的プロセスでの階乗 ; ; ! : number -> number ; ; to compute n*(n-1)*. . . *2*1 ; ; (! 4) = 24 終了条件 (define (! n) (factorial 1 1 n)) (define (factorial product counter n) (cond 自明な解 [(> counter n) product] [else (factorial (* counter product) (+ counter 1) n)]))

終了条件 (> counter n) Yes No (factorial (* counter product) (+ counter 1) n) product が自明の解

反復的プロセスでの再帰 • factorial の内部に factorial が登場 (define (factorial product counter n) (cond [(> counter n) product] [else (factorial (* counter product) (+ counter 1) n)])) • factorial の実行が繰り返される 例： (factorial 6 4 10) = (factorial 24 5 10) = (factorial 120 6 10) ⇒　まさに「再帰」である

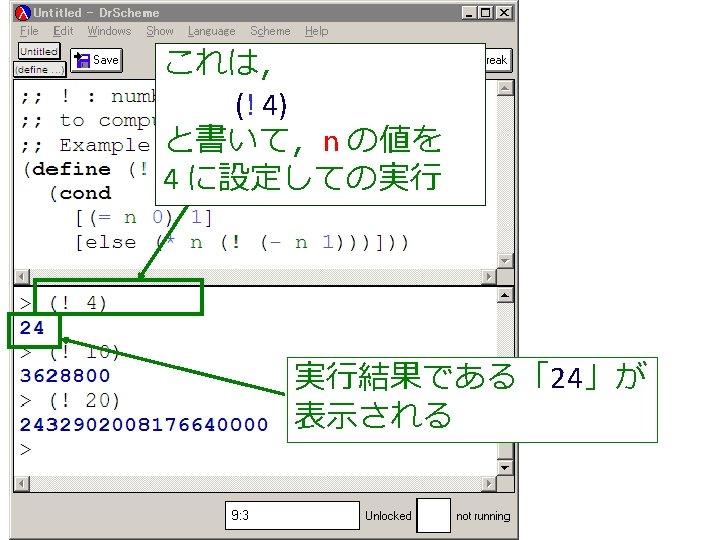
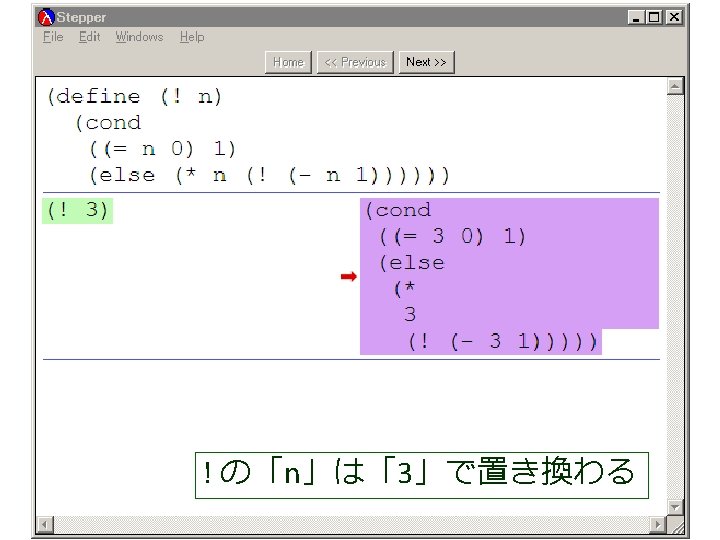
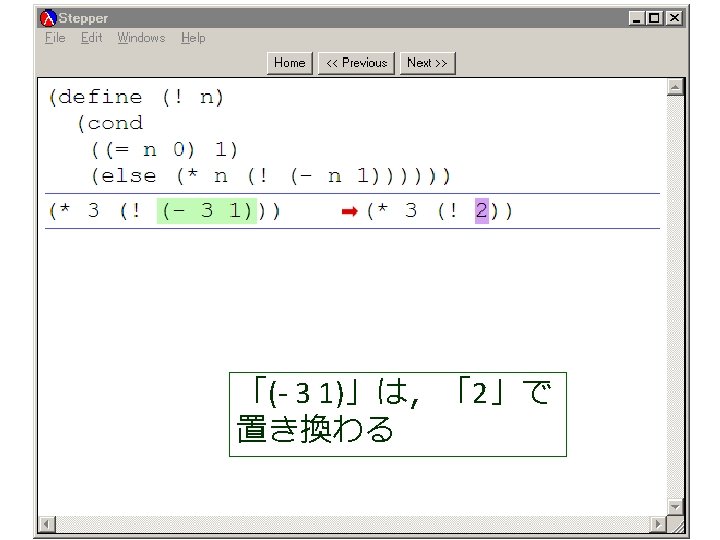
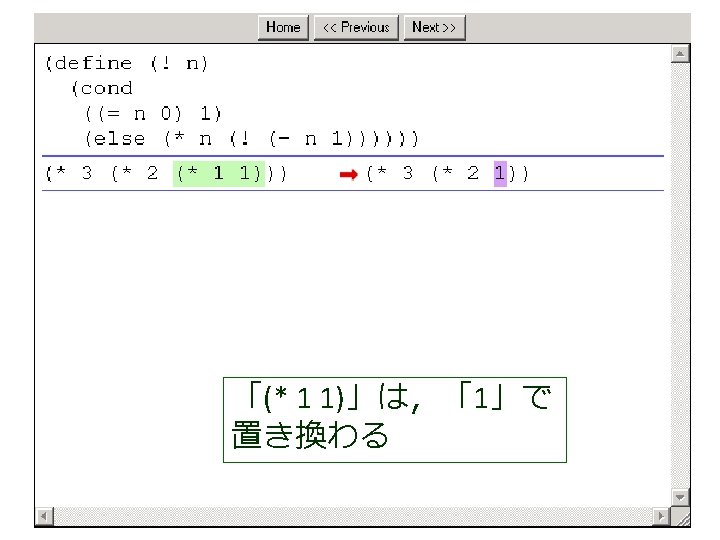
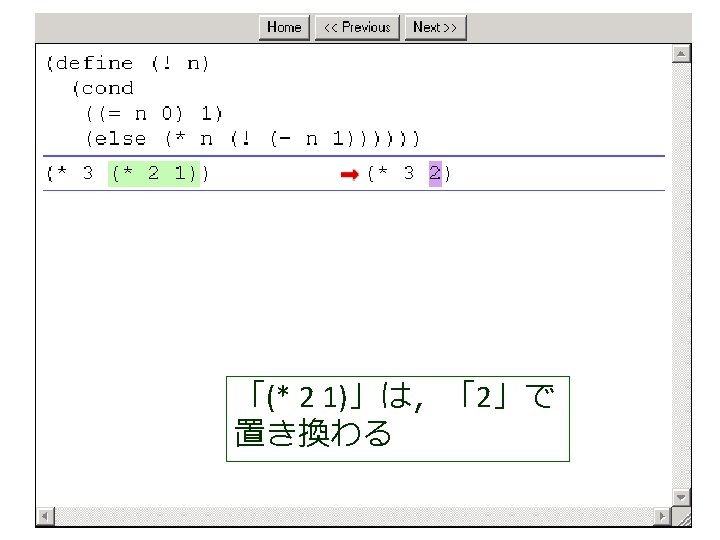
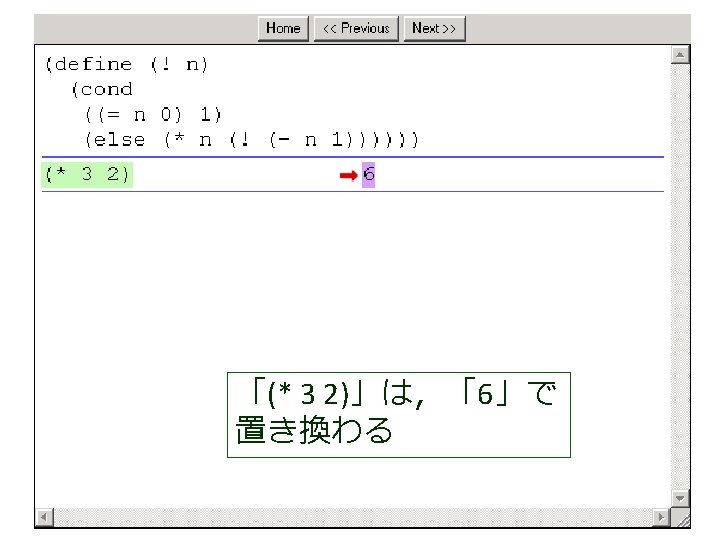
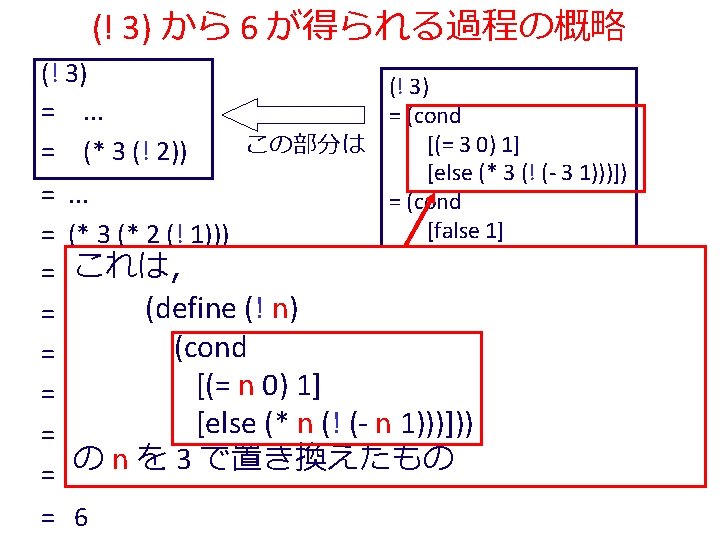
例題４．ステップ実行　 • 関数 ! （例題３）について，実行結果 に至る過程を見る – (! 4) から 24 に至る過程を見る – Dr. Scheme の stepper を使用する (define (factorial product counter n) (cond [(> counter n) product] [else (factorial (* counter product) (+ counter 1) n)])) (! 4) =　(factorial 1 1 4) =　. . . =　(factorial 1 2 4) =　. . . =　(factorial 2 3 4) =　. . . =　(factorial 6 4 4) =　. . . =　(factorial 24 5 4) =　. . . =　24

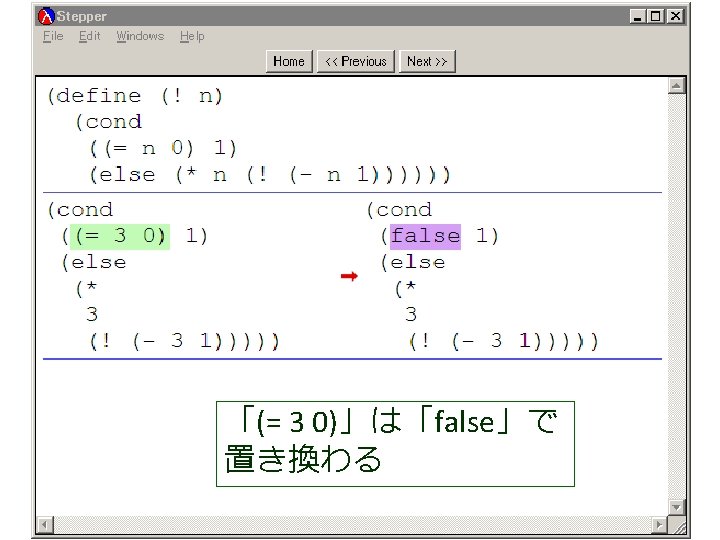
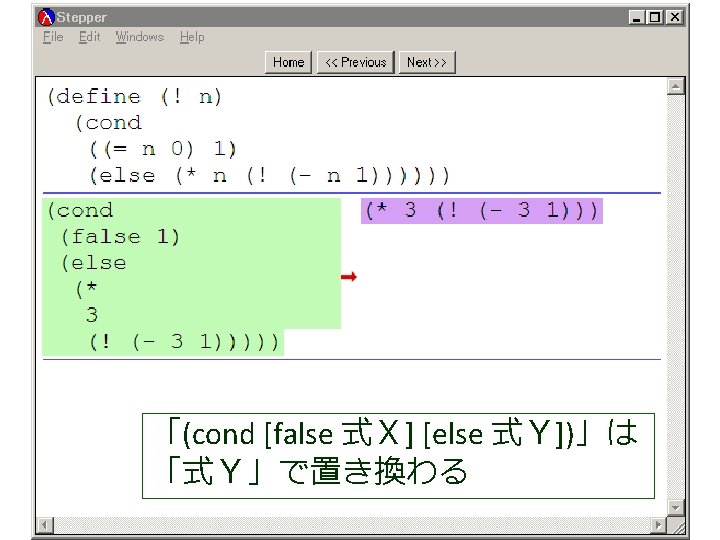
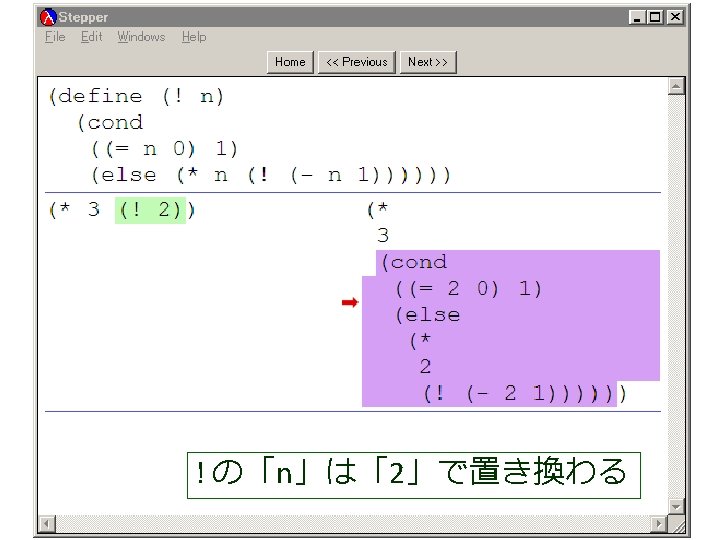
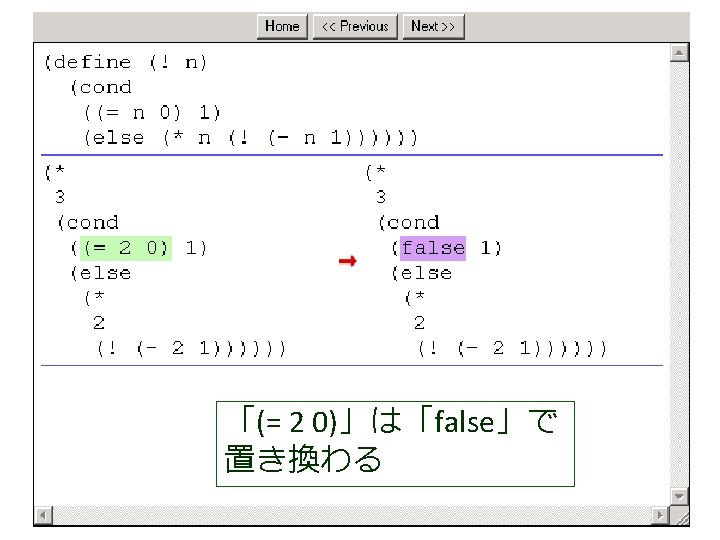
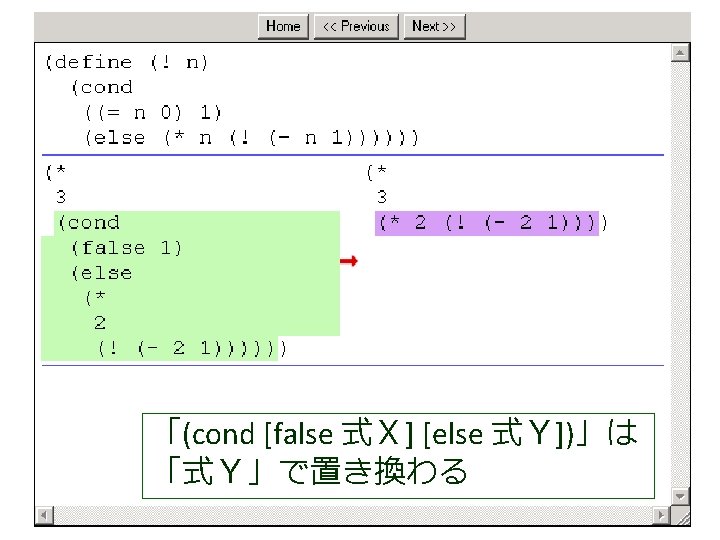
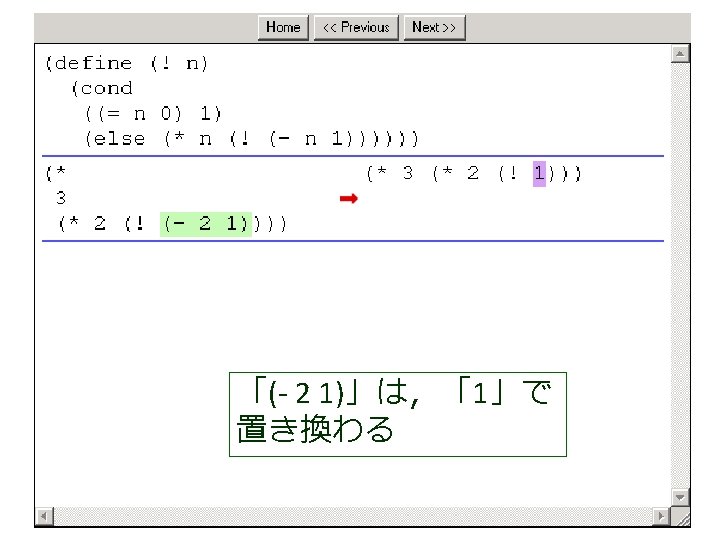
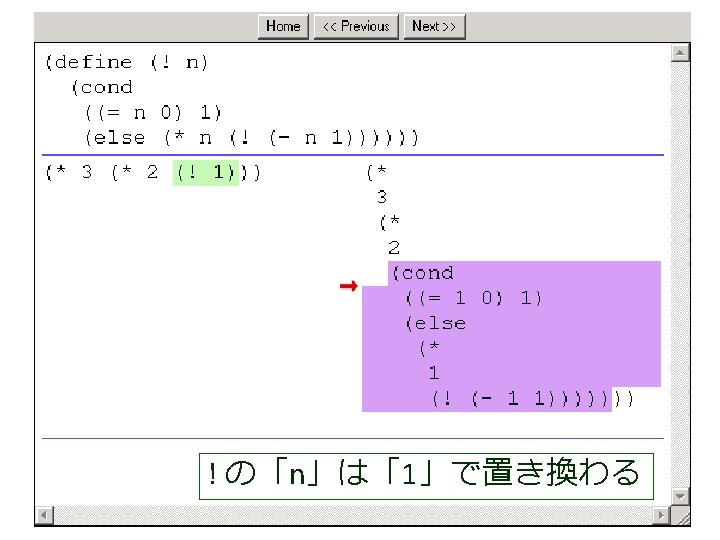
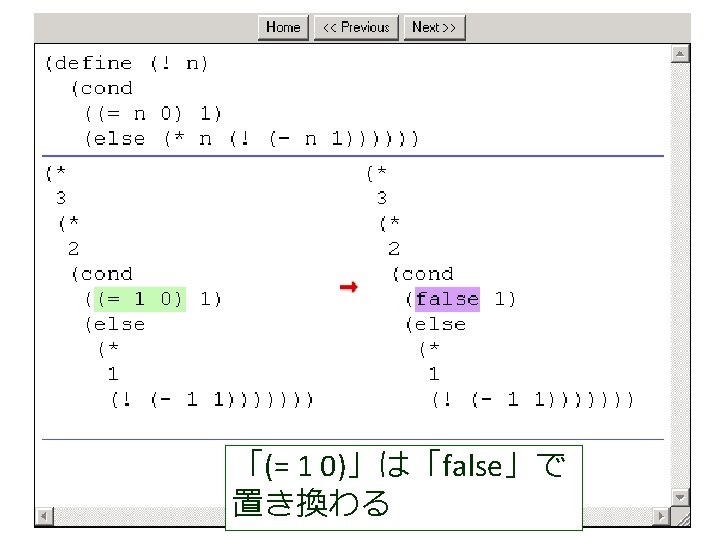
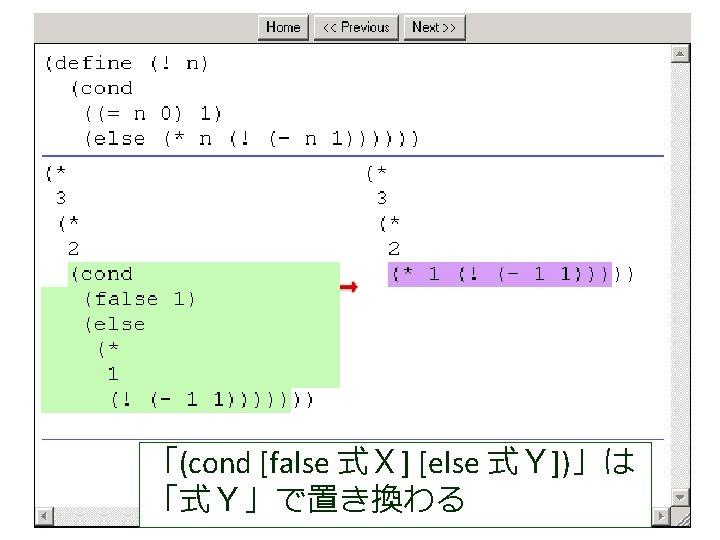
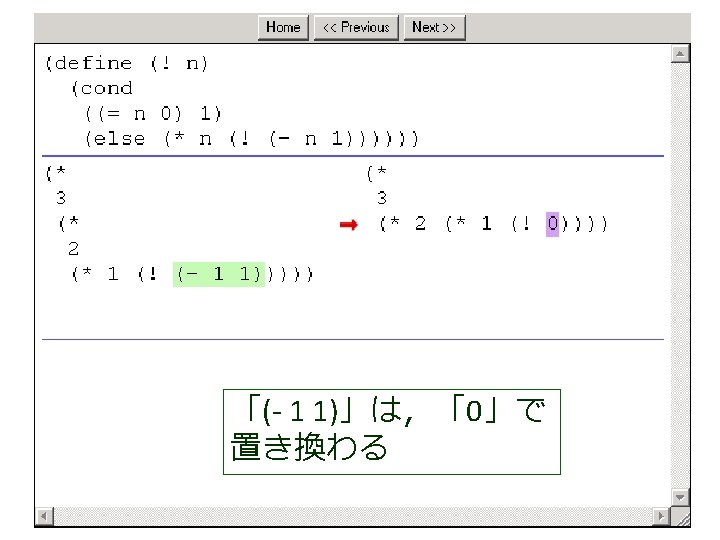
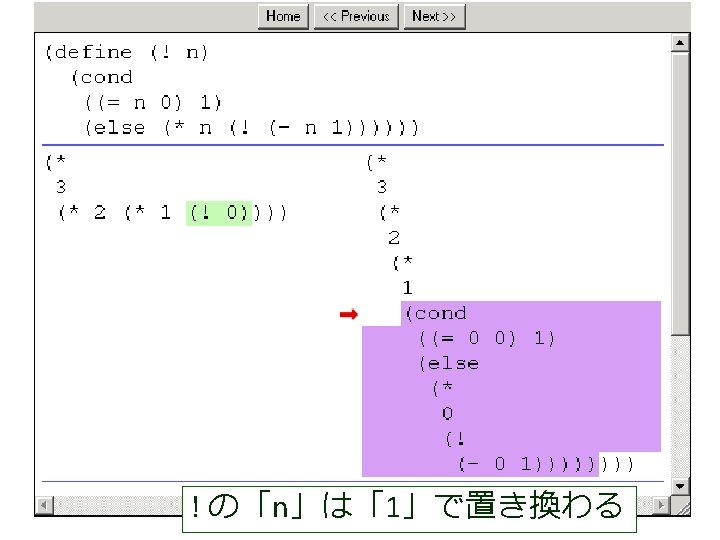
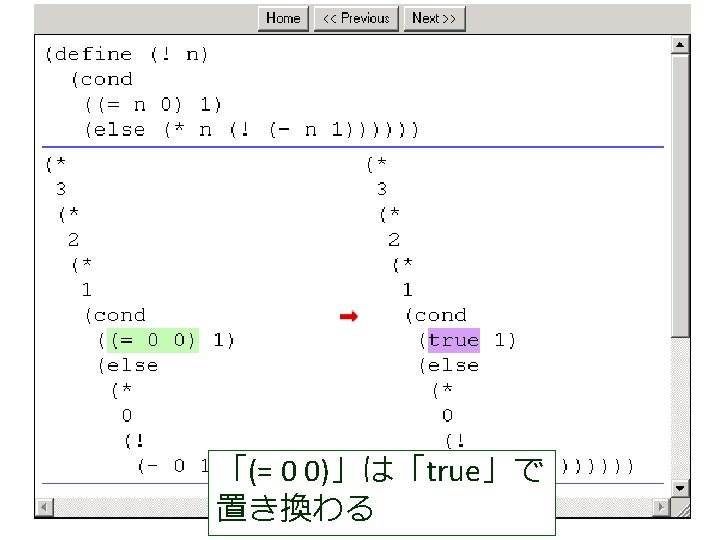
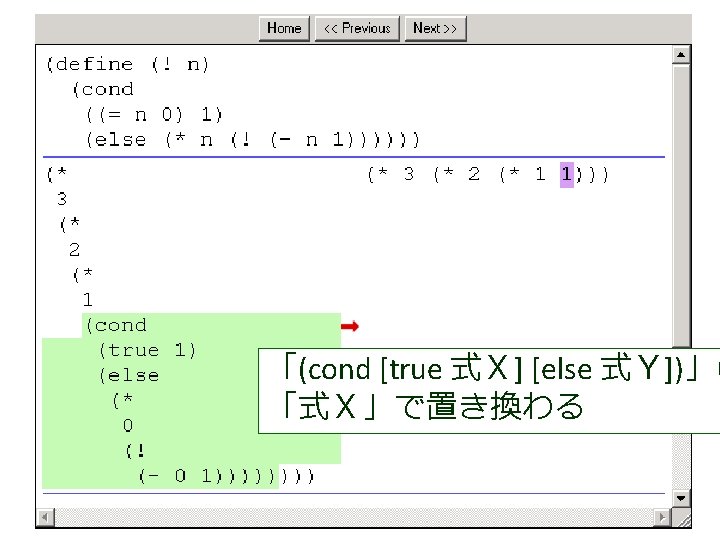
(factorial 1 1 4) から (factorial 1 2 4) が得られる過程 (! 4) (factorial 1 1 4) = (cond =　. . . [(> 1 4) 1] =　(factorial 1 2 4) この部分は [else (factorial (* 1 1) (+ 1 1) =　. . . 4)]) =　(factorial 2 3 4) = (cond [false 1] =　. . . [else (factorial (* 1 1) =　(factorial 6 4 4) (+ 1 1) 4)]) =　. . . = (factorial (* 1 1) (+ 1 1) 4) =　(factorial 24 5 4) = (factorial 1 (+ 1 1) 4) =　. . . = (factorial 1 2 4) =　24

(factorial 1 1 4) から (factorial 1 2 4) が得られる過程 (! 4) (factorial 1 1 4) = (cond =　. . . [(> 1 4) 1] =　(factorial 1 2 4) この部分は [else (factorial (* 1 1) (+ 1 1) =　. . . 4)]) =　(factorial 2 3 4) = (cond これは， [false 1] =　. . . (define (factorial product counter n) (factorial (* 1 1) [else =　(factorial (cond 6 4 4) (+ 1 1) [(> counter n) product] 4)]) =　. . . [else (factorial (* counter product)(* 1 1) (+ 1 1) 4) = (factorial =　(factorial 24 5 4)(+ counter 1) = (factorial 1 (+ 1 1) 4) n)])) =　. . . = (factorial 1 2 4) の counter を 1 で，product を 1 で，n を 4 で置き換えたも =　24 の

例題５．繰り返し回数 • 次のプログラムでは，square は何回実行される か (define (square x) (* x x)) (define (total-square x) (cond [(empty? x) 0] [else (+ (square (first x)) (total-square (rest x)))]))

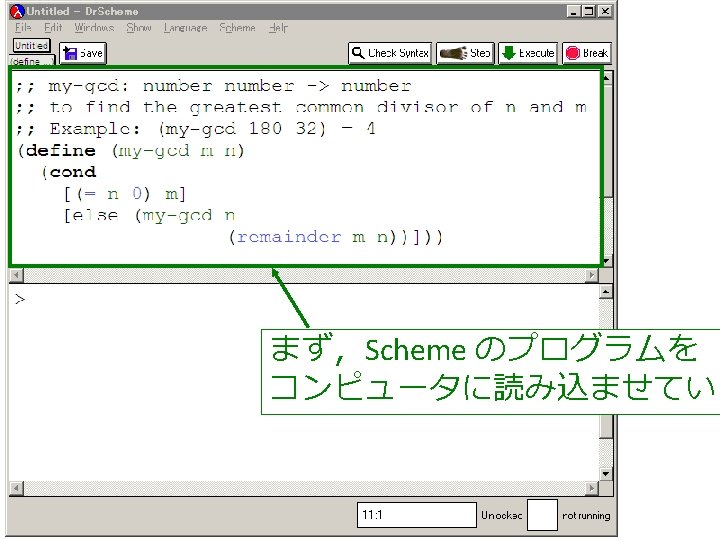
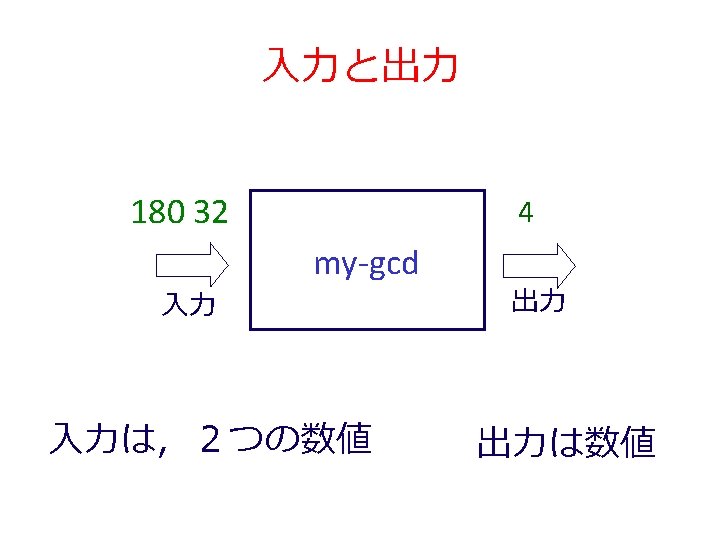
my-gcd 関数 ; ; my-gcd: number -> number ; ; to find the greatest common divisor of n and m ; ; Example: (my-gcd 180 32) = 4 (define (my-gcd m n) (cond [(= n 0) m] [else (my-gcd n (remainder m n))]))

; ; my-gcd: number -> number ; ; to find the greatest common divisor of n and m ; ; Example: (my-gcd 180 32) = 4 (define (my-gcd m n) (cond 終了 自明な解 [(= n 0) m] 条件 [else (my-gcd n (remainder m n))]))

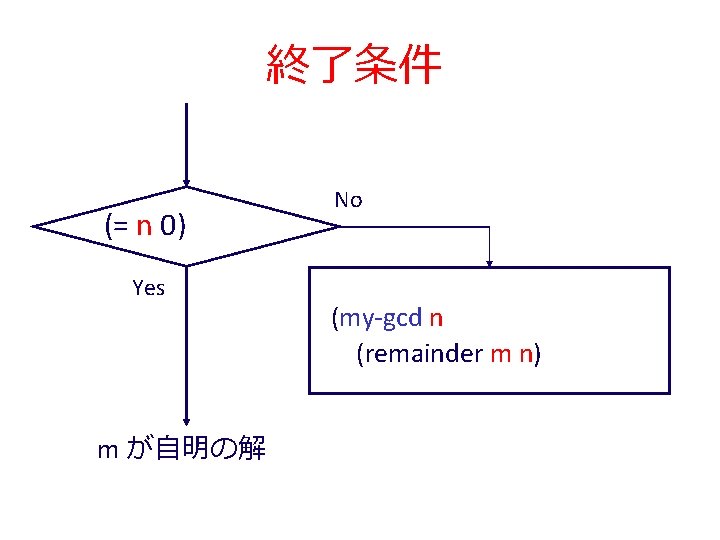
終了条件 (= n 0) Yes m が自明の解 No (my-gcd n (remainder m n)

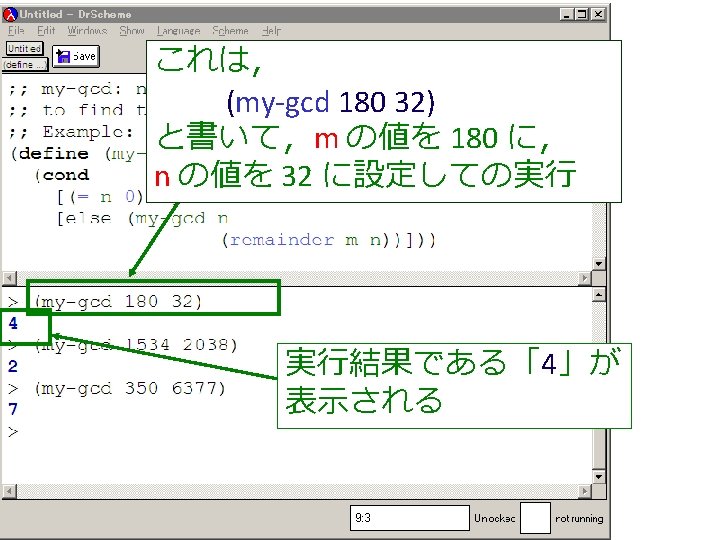
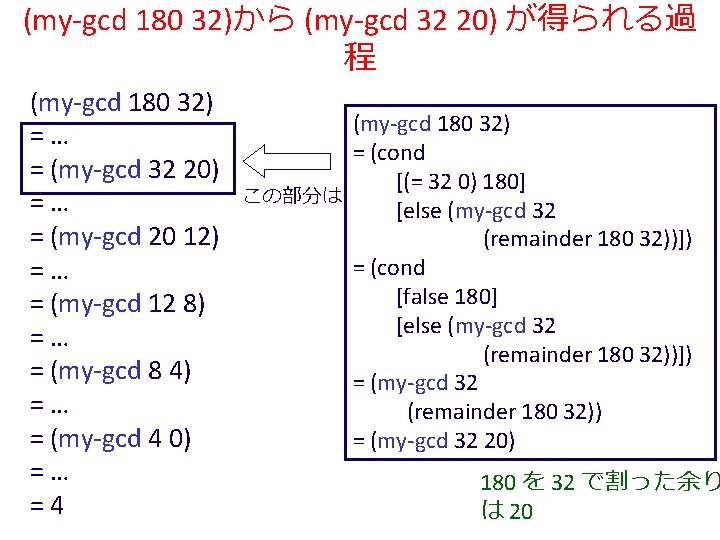
(my-gcd 180 32)から (my-gcd 32 20) が得られる過 程 (my-gcd 180 32) =… = (my-gcd 32 20) =… = (my-gcd 20 12) =… = (my-gcd 12 8) =… = (my-gcd 8 4) =… = (my-gcd 4 0) =… =4 (my-gcd 180 32) = (cond [(= 32 0) 180] この部分は [else (my-gcd 32 (remainder 180 32))]) = (cond [false 180] [else (my-gcd 32 (remainder 180 32))]) = (my-gcd 32 (remainder 180 32)) = (my-gcd 32 20) 180 を 32 で割った余り は 20

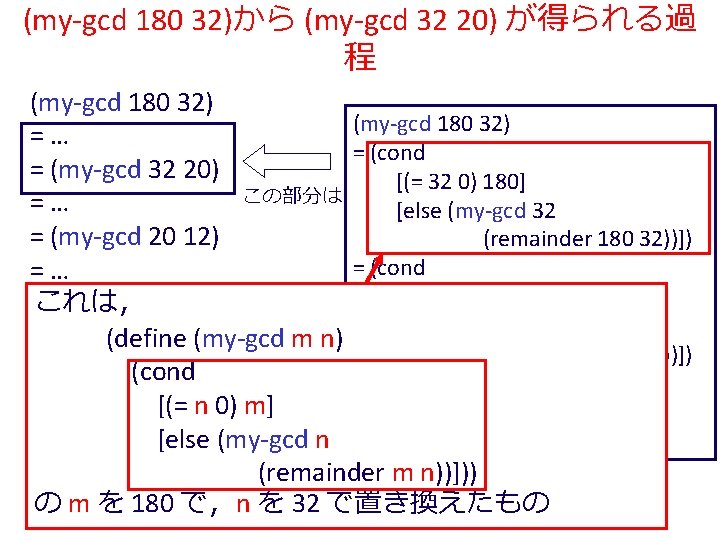
(my-gcd 180 32)から (my-gcd 32 20) が得られる過 程 (my-gcd 180 32) =… = (cond = (my-gcd 32 20) [(= 32 0) 180] この部分は =… [else (my-gcd 32 = (my-gcd 20 12) (remainder 180 32))]) = (cond =… [false 180] =これは， (my-gcd 12 8) [else (my-gcd 32 = … (define (my-gcd m n) (remainder 180 32))]) = (my-gcd(cond 8 4) = (my-gcd 32 =… [(= n 0) m] (remainder 180 32)) = (my-gcd 4[else 0) (my-gcd n = (my-gcd 32 20) =… (remainder m n))])) =の 4 m を 180 で，n を 32 で置き換えたもの