Introduction to Quantum Information Processing QIC 710 CS

Introduction to Quantum Information Processing QIC 710 / CS 768 / PH 767 / CO 681 / AM 871 Lecture 22 -23 (2019) Richard Cleve QNC 3129 cleve@uwaterloo. ca 1 © Richard Cleve 2020

Communication complexity 2 © Richard Cleve 2020

Classical communication complexity [Yao, 1979] x 1 x 2 xn y 1 y 2 yn f (x, y) E. g. equality function: f (x, y) = 1 if x = y, and 0 if x y Question: can the communication be less than n bits? 3 © Richard Cleve 2020

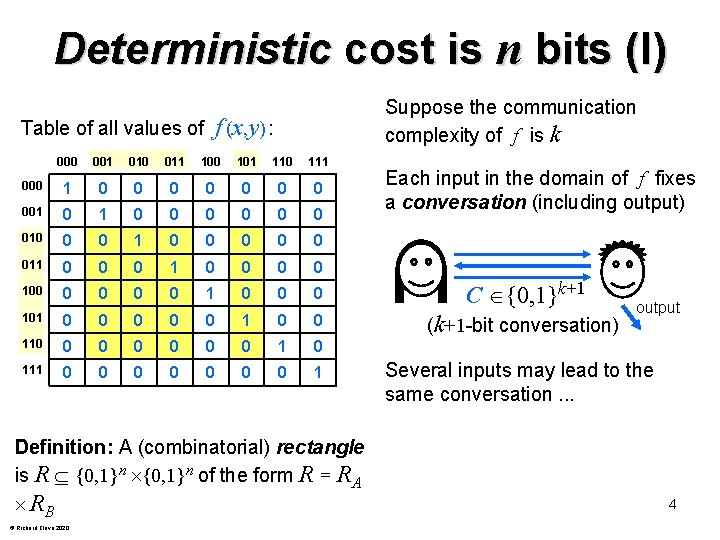
Deterministic cost is n bits (I) Suppose the communication complexity of f is k f (x, y) : Table of all values of 000 001 010 011 100 101 110 111 000 1 0 0 0 001 0 0 0 0 010 0 0 1 0 0 011 0 0 0 0 100 0 0 1 0 0 0 C {0, 1}k+1 101 0 0 0 1 0 0 (k+1 -bit conversation) 110 0 0 0 1 0 111 0 0 0 0 1 Definition: A (combinatorial) rectangle is R {0, 1}n of the form R = RA RB © Richard Cleve 2020 Each input in the domain of f fixes a conversation (including output) output Several inputs may lead to the same conversation. . . 4

Deterministic cost is n bits (II) f (x, y) : Table of all values of 000 001 010 011 100 101 110 111 000 1 0 0 0 001 0 0 0 0 010 0 0 1 0 0 011 0 0 0 0 100 0 0 101 0 0 0 110 0 0 0 1 0 111 0 0 0 0 1 In fact, the inputs leading to C must constitute a rectangle: if (x, y), (x', y') both lead to C then so do (x', y) and (x, y') Since each conversation has a unique output, f is constant on each of these rectangles Need at least 2 n+1 rectangles to {0, 1}-partition this table Since this implies 2 n+1 distinct conversations, k n Therefore, the deterministic communication complexity is n © Richard Cleve 2020 5

Probabilistic cost is O(log n) bits Start with a “good” classical error-correcting code, which is a function {0, 1}n {0, 1}cn such that, for all x ≠ y, Δ(e(x), e( y)) δcn where e: (Δ means Hamming distance), c, δ are constants x 1 x 2 xn randomly choose r {1, 2, . . . , cn} (r, e(x) ) r y 1 y 2 yn output 1 if e( y)r = e(x)r 0 if e( y)r e(x)r e(x) = 1 0 1 1 1 0 0 1 e(y) = 0 1 1 0 0 1 0 Can repeat to reduce error © Richard Cleve 2020 random k 6

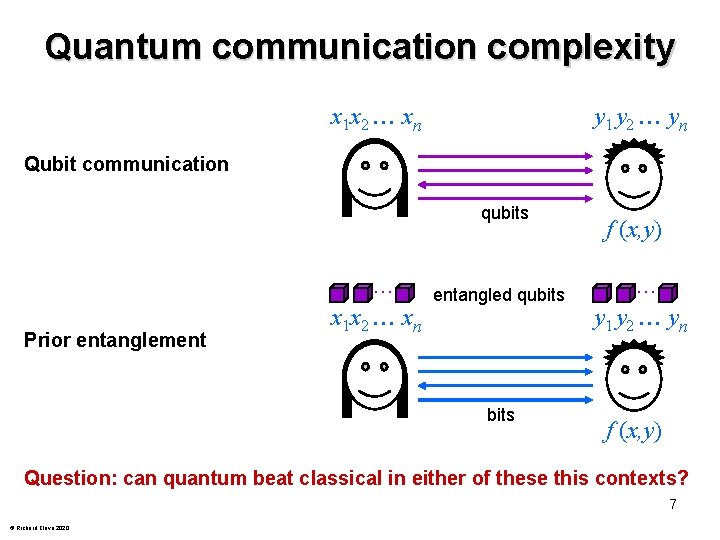
Quantum communication complexity x 1 x 2 xn y 1 y 2 yn Qubit communication qubits Prior entanglement x 1 x 2 xn entangled qubits f (x, y) y 1 y 2 yn f (x, y) Question: can quantum beat classical in either of these this contexts? 7 © Richard Cleve 2020

Appointment scheduling (also known as the Disjointness Problem) 1 2 3 4 5 . . . n x= 01101… 0 1 2 3 4 5 . . . n y= 10011… 1 i (xi = yi = 1) Classically, (n) bits necessary to succeed with prob. 3/4 For all > 0, O(n 1/2 log n) qubits sufficient for error prob. < [KS ‘ 87] [BCW ‘ 98] © Richard Cleve 2020 8

Search problem 1 Given: 2 3 4 5 6 . . . n x= 000010… 1 log n i 1 b x accessible via queries i bb xxii Goal: find i {1, 2, …, n} such that xi = 1 Classically: (n) queries are necessary Quantum mechanically: O(n 1/2) queries are sufficient [Grover, 1996] © Richard Cleve 2020 9

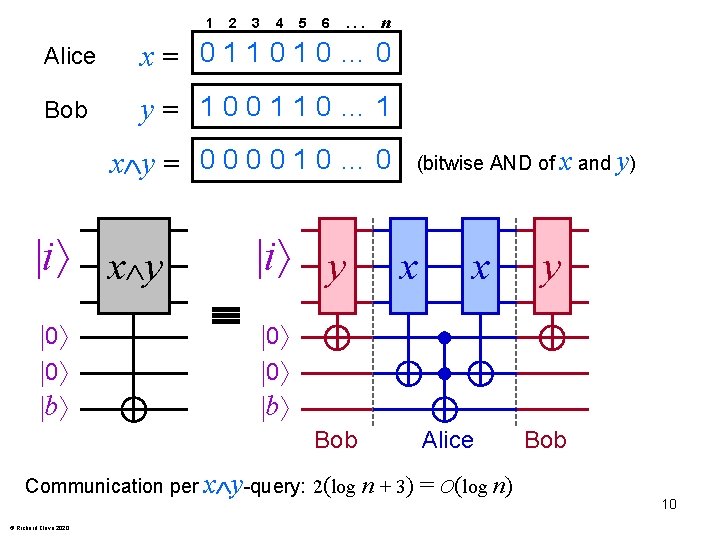
1 2 3 4 5 6 . . . n Alice x= 011010… 0 Bob y= 100110… 1 x y = 0 0 1 0 … 0 i x y 0 0 b i y x x y 0 0 b Bob Communication per x y-query: 2(log © Richard Cleve 2020 (bitwise AND of x and y) Alice n + 3) = O(log n) Bob 10

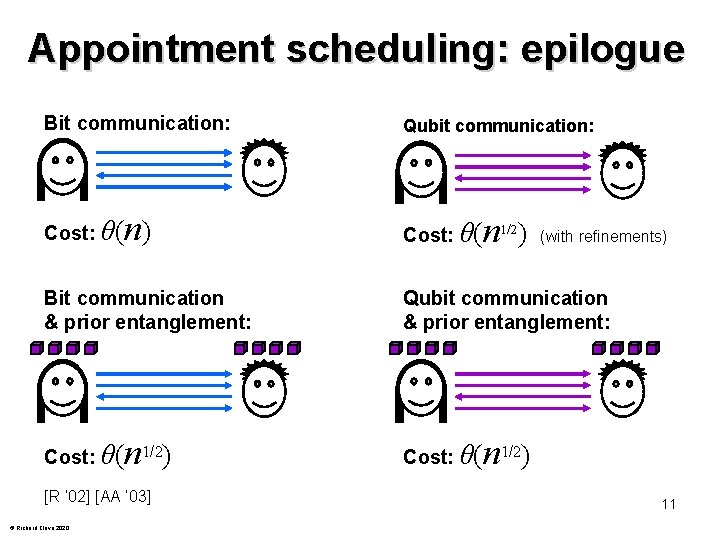
Appointment scheduling: epilogue Bit communication: Cost: θ( n) Bit communication & prior entanglement: Cost: θ( n 1/2) [R ‘ 02] [AA ‘ 03] © Richard Cleve 2020 Qubit communication: Cost: θ( n 1/2 ) (with refinements) Qubit communication & prior entanglement: Cost: θ( n 1/2) 11

Quantum fingerprinting 12 © Richard Cleve 2020

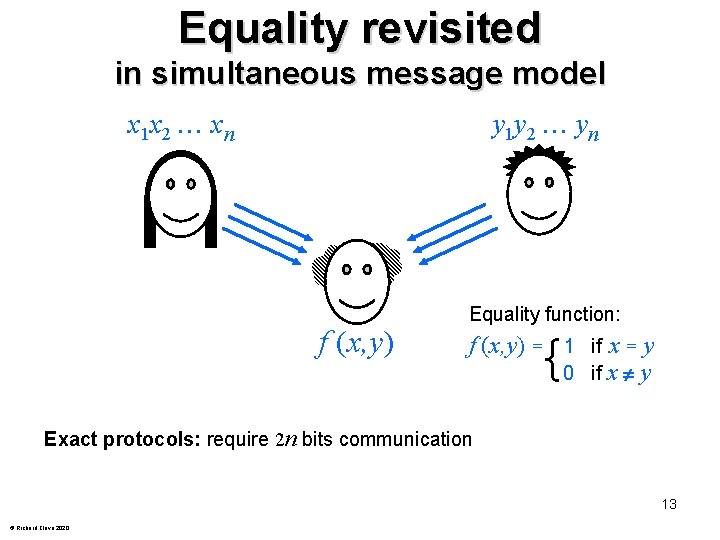
Equality revisited in simultaneous message model x 1 x 2 xn y 1 y 2 yn f (x, y) Equality function: f (x, y) = 1 if x = y 0 if x y Exact protocols: require 2 n bits communication 13 © Richard Cleve 2020

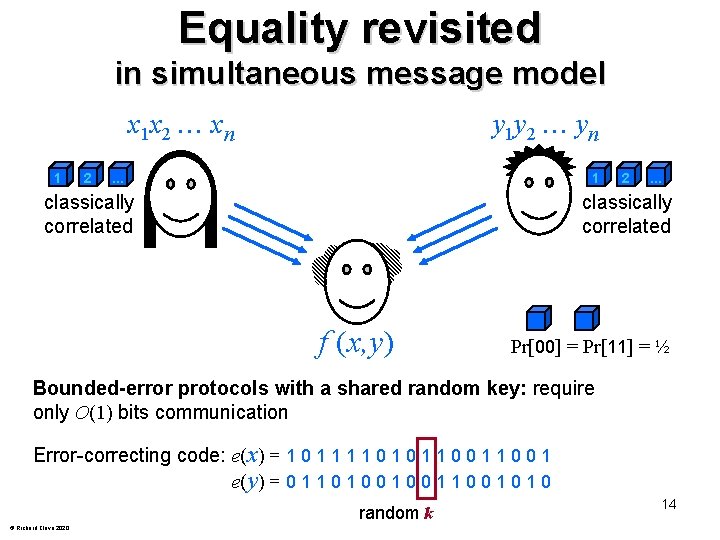
Equality revisited in simultaneous message model x 1 x 2 xn 1 2 y 1 y 2 yn . . . 1 classically correlated 2 . . . classically correlated f (x, y) Pr[00] = Pr[11] = ½ Bounded-error protocols with a shared random key: require only O(1) bits communication Error-correcting code: e(x) = 1 0 1 1 0 0 1 e(y) = 0 1 1 0 0 1 0 1 0 random k © Richard Cleve 2020 14

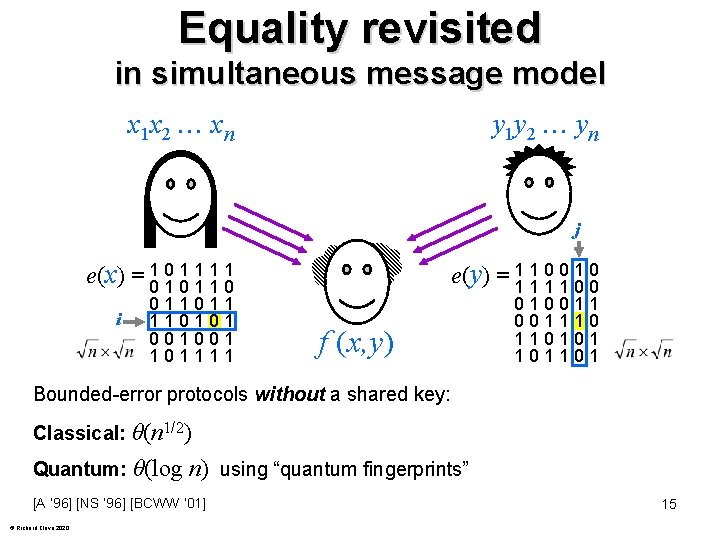
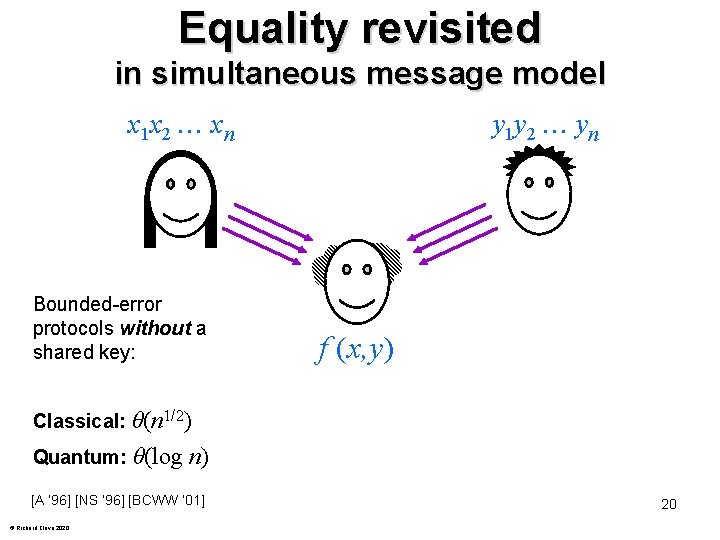
Equality revisited in simultaneous message model x 1 x 2 xn y 1 y 2 yn j e(y) = 11 11 10 10 01 00 e(x) = 01 10 01 11 11 01 i 011011 110101 001001 101111 f (x, y) 01001110 110101 101101 Bounded-error protocols without a shared key: Classical: θ(n 1/2) Quantum: θ(log n) using “quantum fingerprints” [A ‘ 96] [NS ‘ 96] [BCWW ‘ 01] © Richard Cleve 2020 15

Quantum fingerprints Question 1: how many orthogonal states in m qubits? Answer: 2 m Let be an arbitrarily small positive constant Question 2: how many almost orthogonal* states in m qubits? (* where | x y | ≤ ) am Answer: 22 , for some constant 0 a 1 Construction of almost orthogonal states: states start with a special classical error-correcting code, which is a function e : {0, 1}n {0, 1}cn such that, for all x ≠ y, δcn ≤ Δ(e(x), e(y)) ≤ (1− δ )cn (c, δ are constants) 16 © Richard Cleve 2020

Construction of almost orthogonal states for each x {0, 1}n (log(cn) qubits) Set x Then x y Since δcn ≤ Δ(e(x), e(y)) ≤ (1− δ )cn, we have | x y | ≤ 1− 2δ By duplicating each state, x x … x , the pairwise inner products can be made arbitrarily small: (1− 2δ )r ≤ Result: m = r log(cn) qubits storing 2 n = 2(1/c)2 (as opposed to n qubits!) © Richard Cleve 2020 m/r different states 17

What are these almost orthogonal states good for? Question 3: can they be used to somehow store n bits using only O(log n) qubits? Answer: No — recall that Holevo’s theorem forbids this Here’s what we can do: given two states from an almost orthogonal set, we can distinguish between these two cases: • they’re both the same state • they’re almost orthogonal Question 4: How? 18 © Richard Cleve 2020

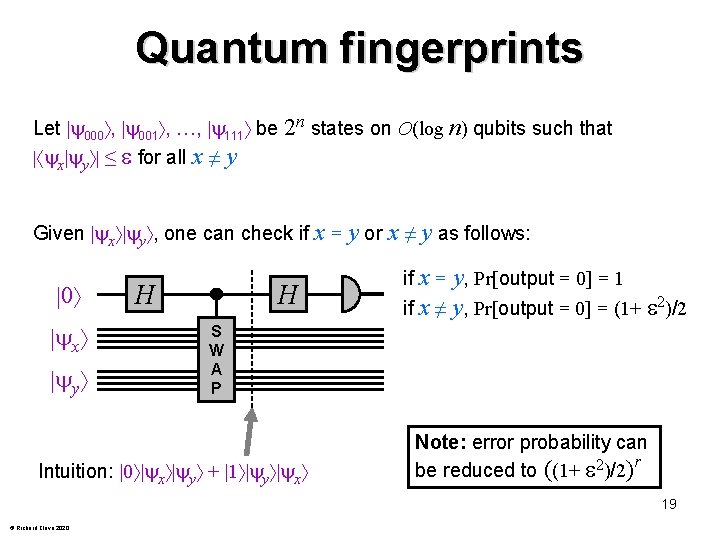
Quantum fingerprints Let 000 , 001 , …, 111 be 2 n states on O(log n) qubits such that | x y | ≤ for all x ≠ y Given x y , one can check if x = 0 x y H H y or x ≠ y as follows: if x = y, Pr[output = 0] = 1 if x ≠ y, Pr[output = 0] = (1+ 2)/2 S W A P Intuition: 0 x y + 1 y x Note: error probability can be reduced to ((1+ 2)/2)r 19 © Richard Cleve 2020

Equality revisited in simultaneous message model x 1 x 2 xn Bounded-error protocols without a shared key: y 1 y 2 yn f (x, y) Classical: θ(n 1/2) Quantum: θ(log n) [A ‘ 96] [NS ‘ 96] [BCWW ‘ 01] © Richard Cleve 2020 20

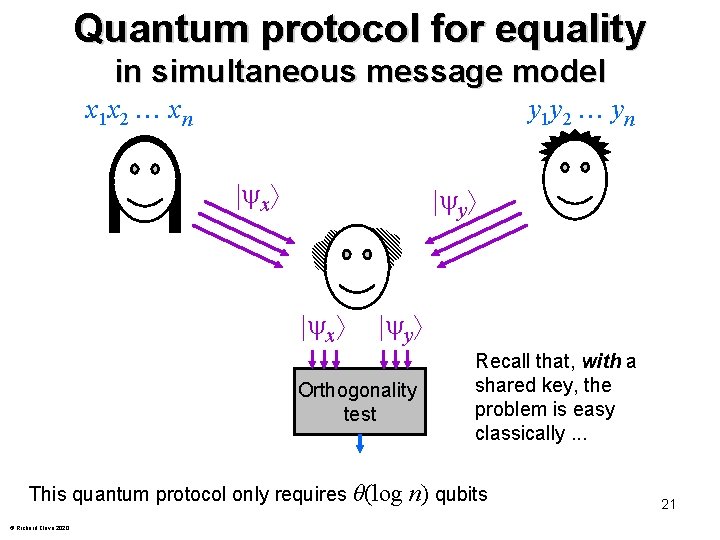
Quantum protocol for equality in simultaneous message model x 1 x 2 xn y 1 y 2 yn x y Orthogonality test Recall that, with a shared key, the problem is easy classically. . . This quantum protocol only requires θ(log n) qubits © Richard Cleve 2020 21

Inner product 22 © Richard Cleve 2020

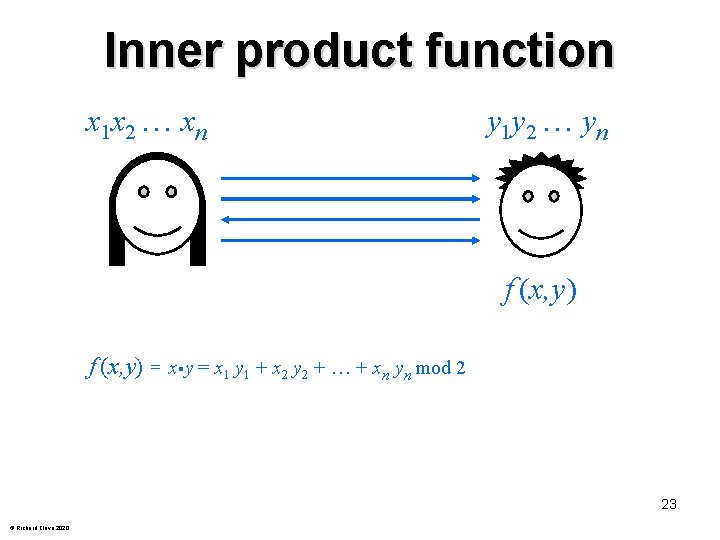
Inner product function x 1 x 2 xn y 1 y 2 yn f (x, y) = x・y = x 1 y 1 + x 2 y 2 + + xn yn mod 2 23 © Richard Cleve 2020

Aside: Bernstein-Vazirani problem I Let f (x 1, x 2, …, xn) = a 1 x 1 + a 2 x 2 + + an xn mod 2 Given: x 1 x 2 xn b Goal: determine a 1, a 2 , f x 1 x 2 with unknown a 1, a 2 , …, an xn b f (x 1, x 2, …, xn) …, an Classically, n queries are necessary 24 © Richard Cleve 2020

Aside: Bernstein-Vazirani problem II Let f (x 1, x 2, …, xn) = a 1 x 1 + a 2 x 2 + + an xn mod 2 Given: 0 0 0 1 H H H Goal: determine a 1, a 2 , f H H H a 1 a 2 an 1 …, an Classically, n queries are necessary Quantum mechanically, 1 query is sufficient 25 © Richard Cleve 2020

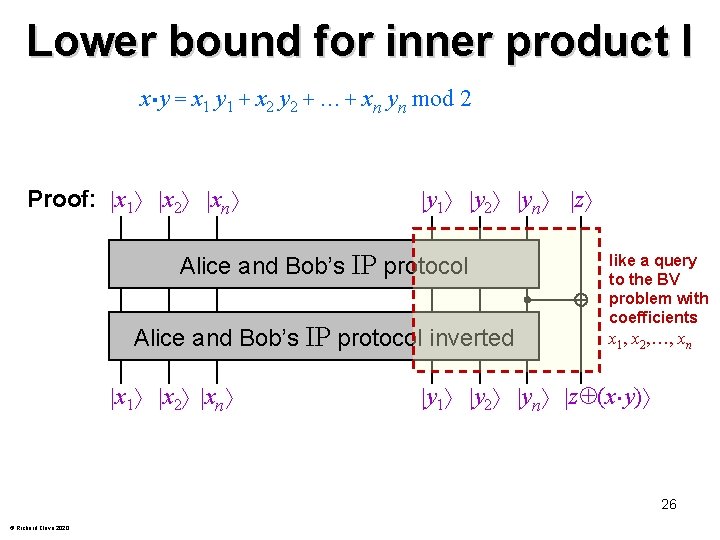
Lower bound for inner product I x・y = x 1 y 1 + x 2 y 2 + + xn yn mod 2 Proof: x 1 x 2 xn y 1 y 2 yn z Alice and Bob’s IP protocol inverted x 1 x 2 xn like a query to the BV problem with coefficients x 1, x 2, …, xn y 1 y 2 yn z (x・y) 26 © Richard Cleve 2020

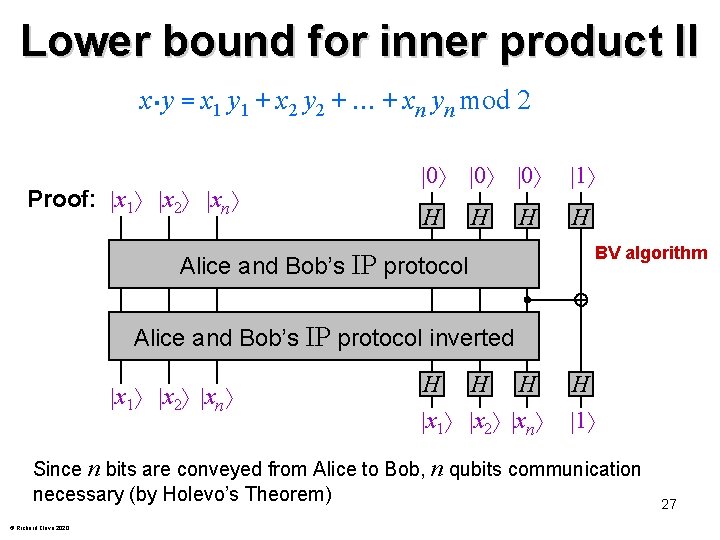
Lower bound for inner product II x・y = x 1 y 1 + x 2 y 2 + + xn yn mod 2 Proof: x 1 x 2 xn 0 0 0 1 H H Alice and Bob’s IP protocol BV algorithm Alice and Bob’s IP protocol inverted x 1 x 2 xn H H H x 1 x 2 xn H 1 Since n bits are conveyed from Alice to Bob, n qubits communication necessary (by Holevo’s Theorem) © Richard Cleve 2020 27