Interest Rate Derivatives Model of the Short Rate

  • Slides: 26
Download presentation
Interest Rate Derivatives: Model of the Short Rate Chapter 30 Options, Futures, and Other

Interest Rate Derivatives: Model of the Short Rate Chapter 30 Options, Futures, and Other Derivatives, 7 th Edition, Copyright © John C. Hull 2008 1

Term Structure Models Black’s model is concerned with describing the probability distribution of a

Term Structure Models Black’s model is concerned with describing the probability distribution of a single variable at a single point in time A term structure model describes the evolution of the whole yield curve Options, Futures, and Other Derivatives, 7 th Edition, Copyright © John C. Hull 2008 2

The Zero Curve The process for the instantaneous short rate, r, in the traditional

The Zero Curve The process for the instantaneous short rate, r, in the traditional risk-neutral world defines the process for the whole zero curve in this world If P(t, T ) is the price at time t of a zerocoupon bond maturing at time T where and T is the average r between times t Options, Futures, and Other Derivatives, 7 th Edition, Copyright © John C. Hull 2008 3

Equilibrium Models Options, Futures, and Other Derivatives, 7 th Edition, Copyright © John C.

Equilibrium Models Options, Futures, and Other Derivatives, 7 th Edition, Copyright © John C. Hull 2008 4

Mean Reversion (Figure 30. 1, page 683) Interest rate HIGH interest rate has negative

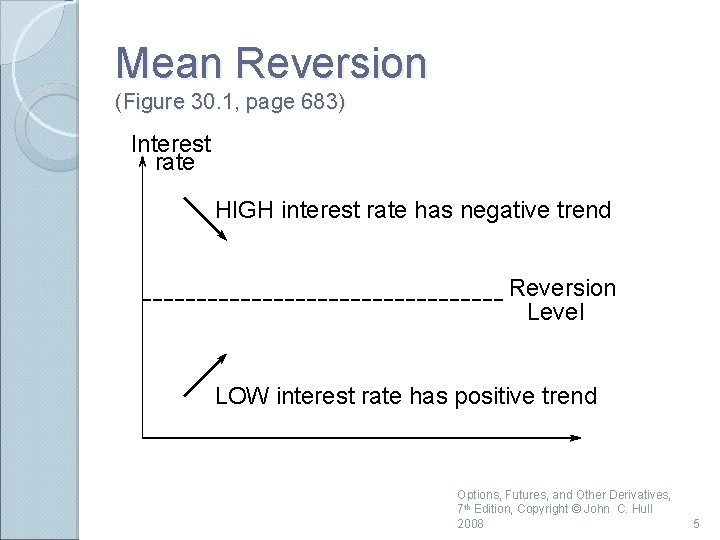
Mean Reversion (Figure 30. 1, page 683) Interest rate HIGH interest rate has negative trend Reversion Level LOW interest rate has positive trend Options, Futures, and Other Derivatives, 7 th Edition, Copyright © John C. Hull 2008 5

Alternative Term Structures in Vasicek & CIR (Figure 30. 2, page 684) Zero Rate

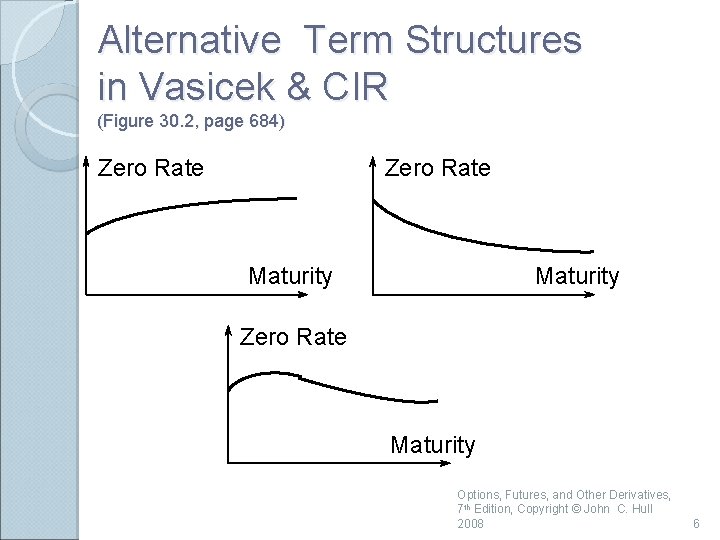
Alternative Term Structures in Vasicek & CIR (Figure 30. 2, page 684) Zero Rate Maturity Options, Futures, and Other Derivatives, 7 th Edition, Copyright © John C. Hull 2008 6

Equilibrium vs No-Arbitrage Models In an equilibrium model today’s term structure is an output

Equilibrium vs No-Arbitrage Models In an equilibrium model today’s term structure is an output In a no-arbitrage model today’s term structure is an input Options, Futures, and Other Derivatives, 7 th Edition, Copyright © John C. Hull 2008 7

Developing No-Arbitrage Model for r A model for r can be made to fit

Developing No-Arbitrage Model for r A model for r can be made to fit the initial term structure by including a function of time in the drift Options, Futures, and Other Derivatives, 7 th Edition, Copyright © John C. Hull 2008 8

Ho-Lee Model dr = q(t)dt + sdz Many analytic results for bond prices and

Ho-Lee Model dr = q(t)dt + sdz Many analytic results for bond prices and option prices Interest rates normally distributed One volatility parameter, s All forward rates have the same standard deviation Options, Futures, and Other Derivatives, 7 th Edition, Copyright © John C. Hull 2008 9

Diagrammatic Representation of Ho-Lee (Figure 30. 3, page 687) Short Rate r r Time

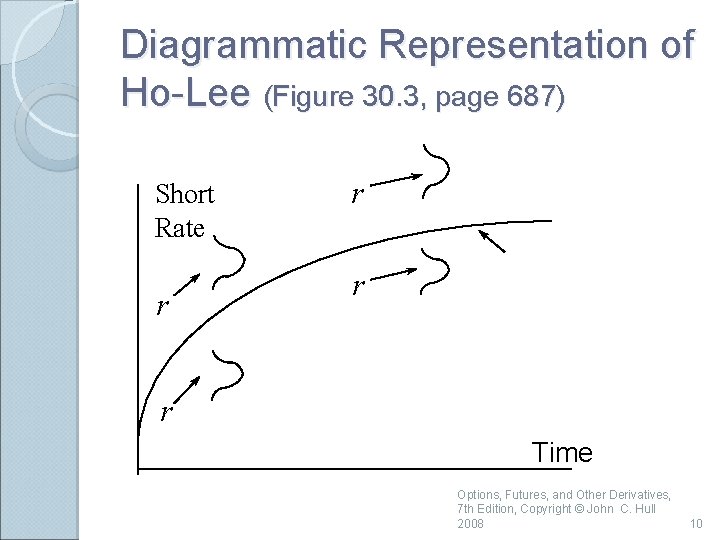
Diagrammatic Representation of Ho-Lee (Figure 30. 3, page 687) Short Rate r r Time Options, Futures, and Other Derivatives, 7 th Edition, Copyright © John C. Hull 2008 10

Hull-White Model dr = [q(t ) – ar ]dt + sdz Many analytic results

Hull-White Model dr = [q(t ) – ar ]dt + sdz Many analytic results for bond prices and option prices Two volatility parameters, a and s Interest rates normally distributed Standard deviation of a forward rate is a declining function of its maturity Options, Futures, and Other Derivatives, 7 th Edition, Copyright © John C. Hull 2008 11

Diagrammatic Representation of Hull and White (Figure 30. 4, page 688) Short Rate r

Diagrammatic Representation of Hull and White (Figure 30. 4, page 688) Short Rate r r Forward Rate Curve Time Options, Futures, and Other Derivatives, 7 th Edition, Copyright © John C. Hull 2008 12

Black-Karasinski Model (equation 30. 18) Future value of r is lognormal Very little analytic

Black-Karasinski Model (equation 30. 18) Future value of r is lognormal Very little analytic tractability Options, Futures, and Other Derivatives, 7 th Edition, Copyright © John C. Hull 2008 13

Options on Zero-Coupon Bonds (equation 30. 20, page 690) In Vasicek and Hull-White model,

Options on Zero-Coupon Bonds (equation 30. 20, page 690) In Vasicek and Hull-White model, price of call maturing at T on a bond lasting to s is LP(0, s)N(h)-KP(0, T)N(h-s. P) Price of put is KP(0, T)N(-h+s. P)-LP(0, s)N(h) where Options, Futures, and Other Derivatives, 7 th Edition, Copyright © John C. Hull 2008 14

Options on Coupon Bearing Bonds In a one-factor model a European option on a

Options on Coupon Bearing Bonds In a one-factor model a European option on a coupon-bearing bond can be expressed as a portfolio of options on zero-coupon bonds. We first calculate the critical interest rate at the option maturity for which the couponbearing bond price equals the strike price at maturity The strike price for each zero-coupon bond is set equal to its value when the interest rate equals this critical value Options, Futures, and Other Derivatives, 7 th Edition, Copyright © John C. Hull 2008 15

Interest Rate Trees vs Stock Price Trees The variable at each node in an

Interest Rate Trees vs Stock Price Trees The variable at each node in an interest rate tree is the Dt-period rate Interest rate trees work similarly to stock price trees except that the discount rate used varies from node to node Options, Futures, and Other Derivatives, 7 th Edition, Copyright © John C. Hull 2008 16

Two-Step Tree Example (Figure 30. 6, page 692) Payoff after 2 years is MAX[100(r

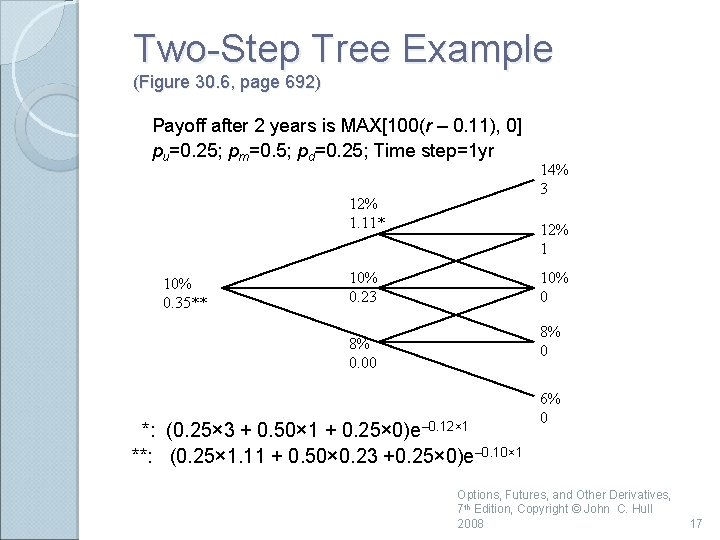
Two-Step Tree Example (Figure 30. 6, page 692) Payoff after 2 years is MAX[100(r – 0. 11), 0] pu=0. 25; pm=0. 5; pd=0. 25; Time step=1 yr 12% 1. 11* 10% 0. 35** 14% 3 12% 1 10% 0. 23 10% 0 8% 0. 00 *: (0. 25× 3 + 0. 50× 1 + 0. 25× 0)e– 0. 12× 1 **: (0. 25× 1. 11 + 0. 50× 0. 23 +0. 25× 0)e– 0. 10× 1 6% 0 Options, Futures, and Other Derivatives, 7 th Edition, Copyright © John C. Hull 2008 17

Alternative Branching Processes in a Trinomial Tree (Figure 30. 7, page 693) (a) (b)

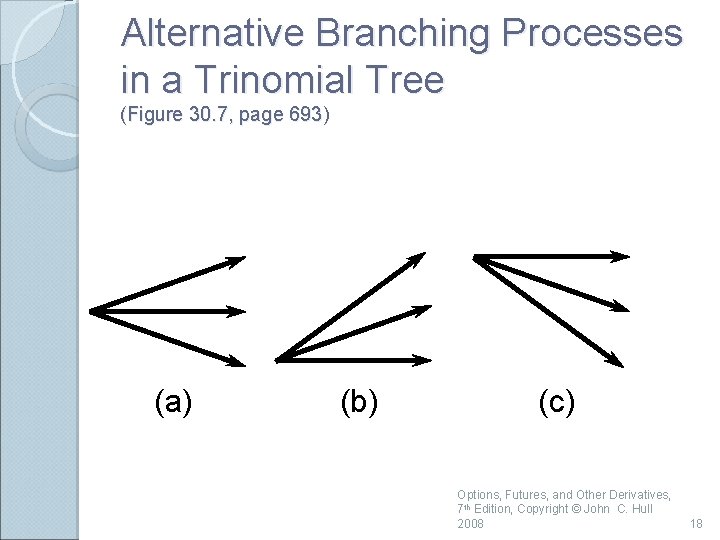
Alternative Branching Processes in a Trinomial Tree (Figure 30. 7, page 693) (a) (b) (c) Options, Futures, and Other Derivatives, 7 th Edition, Copyright © John C. Hull 2008 18

Procedure for Building Tree dr = [q(t ) – ar ]dt + sdz 1.

Procedure for Building Tree dr = [q(t ) – ar ]dt + sdz 1. Assume q(t ) = 0 and r (0) = 0 2. Draw a trinomial tree for r to match the mean and standard deviation of the process for r 3. Determine q(t ) one step at a time so that the tree matches the initial term structure Options, Futures, and Other Derivatives, 7 th Edition, Copyright © John C. Hull 2008 19

Example (page 694 to 699) s = 0. 01 a = 0. 1 Dt

Example (page 694 to 699) s = 0. 01 a = 0. 1 Dt = 1 year The zero curve is as shown in Table 30. 1 on page 697 Options, Futures, and Other Derivatives, 7 th Edition, Copyright © John C. Hull 2008 20

Building the First Tree for the Dt rate R Set vertical spacing: Change branching

Building the First Tree for the Dt rate R Set vertical spacing: Change branching when jmax nodes from middle where jmax is smallest integer greater than 0. 184/(a. Dt) Choose probabilities on branches so that mean change in R is -a. RDt and S. D. of change is Options, Futures, and Other Derivatives, 7 th Edition, Copyright © John C. Hull 2008 21

The First Tree (Figure 30. 8, page 695) E A B F C G

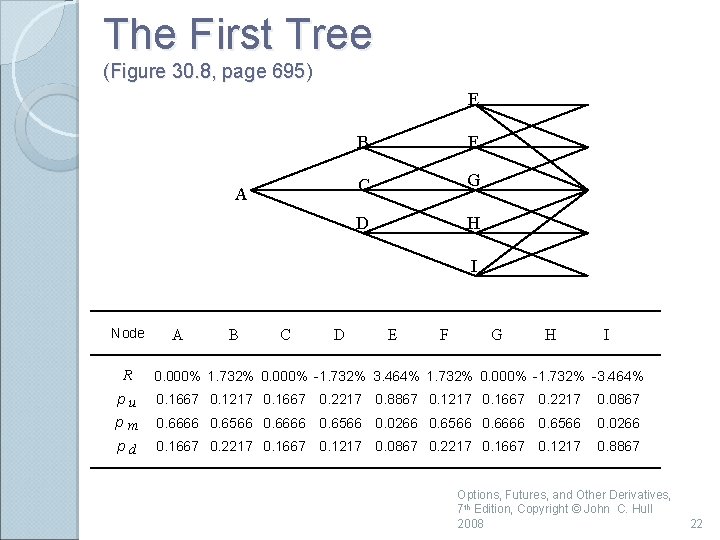
The First Tree (Figure 30. 8, page 695) E A B F C G D H I Node R A B C D E F G H I 0. 000% 1. 732% 0. 000% -1. 732% 3. 464% 1. 732% 0. 000% -1. 732% -3. 464% pu pm 0. 1667 0. 1217 0. 1667 0. 2217 0. 8867 0. 1217 0. 1667 0. 2217 0. 0867 0. 6666 0. 6566 0. 0266 0. 6566 0. 6666 0. 6566 0. 0266 pd 0. 1667 0. 2217 0. 1667 0. 1217 0. 0867 0. 2217 0. 1667 0. 1217 0. 8867 Options, Futures, and Other Derivatives, 7 th Edition, Copyright © John C. Hull 2008 22

Shifting Nodes Work forward through tree Remember Qij the value of a derivative providing

Shifting Nodes Work forward through tree Remember Qij the value of a derivative providing a $1 payoff at node j at time i. Dt Shift nodes at time i. Dt by ai so that the (i+1)Dt bond is correctly priced Options, Futures, and Other Derivatives, 7 th Edition, Copyright © John C. Hull 2008 23

The Final Tree (Figure 30. 9, Page 697) E F B G C A

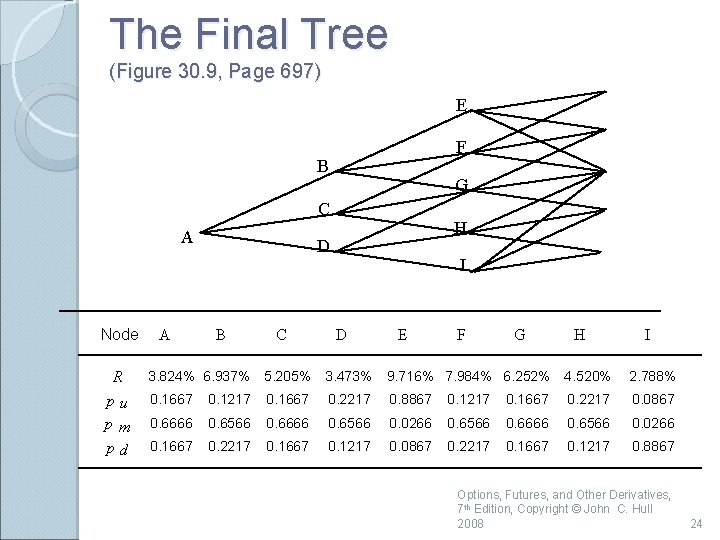
The Final Tree (Figure 30. 9, Page 697) E F B G C A Node R pu pm pd A H D B C I D E F G H I 3. 824% 6. 937% 5. 205% 3. 473% 9. 716% 7. 984% 6. 252% 4. 520% 2. 788% 0. 1667 0. 1217 0. 1667 0. 2217 0. 8867 0. 1217 0. 1667 0. 2217 0. 0867 0. 6666 0. 6566 0. 0266 0. 6566 0. 6666 0. 6566 0. 0266 0. 1667 0. 2217 0. 1667 0. 1217 0. 0867 0. 2217 0. 1667 0. 1217 0. 8867 Options, Futures, and Other Derivatives, 7 th Edition, Copyright © John C. Hull 2008 24

Extensions The tree building procedure can be extended to cover more general models of

Extensions The tree building procedure can be extended to cover more general models of the form: dƒ(r ) = [q(t ) – a ƒ(r )]dt + sdz We set x=f(r) and proceed similarly to before Options, Futures, and Other Derivatives, 7 th Edition, Copyright © John C. Hull 2008 25

Calibration to determine a and s volatility parameters a and s (perhaps functions of

Calibration to determine a and s volatility parameters a and s (perhaps functions of time) are chosen so that the model fits the prices of actively traded instruments such as caps and European swap options as closely as possible We minimize a function of the form The where Ui is the market price of the ith calibrating instrument, Vi is the model price of the ith calibrating instrument and P is a function that penalizes big changes or curvature in a and s Options, Futures, and Other Derivatives, 7 th Edition, Copyright © John C. Hull 2008 26

Interest Rate Derivatives Model of the Short RateInterest Rate Derivatives Model of the Short Rate
Interest Rate Derivatives Models of the Short RateInterest Rate Derivatives Models of the Short Rate
Using Derivatives to Manage Interest Rate Risk DerivativesUsing Derivatives to Manage Interest Rate Risk Derivatives
Section III Derivatives Advanced Topics Interest Rate DerivativesSection III Derivatives Advanced Topics Interest Rate Derivatives
Using Derivatives to Manage Interest Rate Risk DerivativesUsing Derivatives to Manage Interest Rate Risk Derivatives
Using Derivatives to Manage Interest Rate Risk DerivativesUsing Derivatives to Manage Interest Rate Risk Derivatives
Derivatives Interest Rate Derivatives Professor Andr Farber SolvayDerivatives Interest Rate Derivatives Professor Andr Farber Solvay
Chapter 9 Swaps and Interest Rate Derivatives InterestChapter 9 Swaps and Interest Rate Derivatives Interest
Module Derivatives and Related Accounting Issues Derivatives DerivativesModule Derivatives and Related Accounting Issues Derivatives Derivatives
CREDIT DERIVATIVES WHAT ARE CREDIT DERIVATIVES Credit derivativesCREDIT DERIVATIVES WHAT ARE CREDIT DERIVATIVES Credit derivatives
Derivatives part I 1 Derivatives Derivatives are financialDerivatives part I 1 Derivatives Derivatives are financial
Derivatives and Gradients Derivatives Derivatives tell us whichDerivatives and Gradients Derivatives Derivatives tell us which
3 DERIVATIVES DERIVATIVES 3 4 Derivatives of Trigonometric3 DERIVATIVES DERIVATIVES 3 4 Derivatives of Trigonometric
Derivatives part I 1 Derivatives Derivatives are financialDerivatives part I 1 Derivatives Derivatives are financial
Derivatives part I 1 Derivatives Derivatives are financialDerivatives part I 1 Derivatives Derivatives are financial
Interest and Interest Rate Interest amount owed nowInterest and Interest Rate Interest amount owed now
Interest and Interest Rate Interest amount owed nowInterest and Interest Rate Interest amount owed now
short tall tall short short long long shortshort tall tall short short long long short
Interest Rate Options u Interest rate options provideInterest Rate Options u Interest rate options provide
Interest Rate Risk Interest rate changes have significantInterest Rate Risk Interest rate changes have significant
REAL VS NOMINAL INTEREST RATE REAL INTEREST RATEREAL VS NOMINAL INTEREST RATE REAL INTEREST RATE
Duration Measuring Interest Rate Sensitivity Measuring Interest RateDuration Measuring Interest Rate Sensitivity Measuring Interest Rate
Topic 1 Introduction Interest Rate Interest rate rTopic 1 Introduction Interest Rate Interest rate r
Duration Measuring Interest Rate Sensitivity Measuring Interest RateDuration Measuring Interest Rate Sensitivity Measuring Interest Rate